Matières
Niveaux
Le volume des pyramides
Fiche | Mathématiques
Secondaire
3
Avant toute chose, il faut être en mesure de reconnaitre les différentes parties d'une pyramide (base, apothème, hauteur) pour bien l’identifier. Une fois cette étape accomplie, on peut entreprendre le calcul de son volume.
Afin de déterminer l'espace en 3 dimensions qu'une pyramide occupe, on considère d'abord l'aire de sa base pour ensuite la multiplier par la mesure de sa hauteur. Il ne reste qu’à diviser par 3.
||V = \dfrac{A_b \times h}{3}|| où ||\begin{align} A_b &: \text{Aire d'une base}\\ h &: \text{hauteur de la pyramide}\end{align}||
Dans la ville de Québec, une partie d'un édifice commercial est bâtie selon un modèle de pyramide à base carrée.
Afin de respecter les différentes normes, la section pyramidale de cette bâtisse possède une base d'un périmètre de |160\ \text{m}| et une hauteur de |15\ \text{m}.| Si |70\ \%| de cet espace est réservé à des bureaux administratifs, quel espace leur est alors consacré?
-
Identifier la nature du solide
Comme il est écrit dans le problème, il s'agit d'une pyramide à base carrée. -
Appliquer la formule
Étant donné que la base est carrée, on est en mesure de déduire que la mesure d'un côté est de |160 \div 4=40\ \text{m}|.
Ainsi, ||\begin{align} V &=\dfrac{A_b \times h}{3}\\\\&= \dfrac{c^2\times h}{3} \\\\&= \dfrac{40^2 \times 15}{3}\\\\&= 8\ 000\ \text{m}^3 \end{align}|| -
Interpréter la réponse
Puisqu'on s'intéresse à |70\ \%| de cet espace, on obtient : ||70\ \% \times 8\ 000 = 5\ 600\ \text{m}^3||
Ainsi, les locaux administratifs occupent un espace de |5\ 600 \ \text{m}^3.|
Dans certains problèmes, on peut chercher la mesure de la base ou la hauteur de la pyramide alors que le volume est donné. C’est ce qui s’appelle trouver une mesure manquante d'une pyramide à partir du volume. Dans ce cas, la démarche est un peu différente, mais il demeure essentiel de se rappeler la formule du volume associée aux pyramides.
En observant bien sa construction, on voit qu'une des particularités de la pyramide est qu'elle est composée majoritairement de triangles. Ainsi, on peut utiliser cette caractéristique lorsque vient le temps de trouver la mesure de la hauteur ou de l'apothème.
Trouver la mesure de la hauteur d'une pyramide à partir de l’apothème
Il n'y a pas de formule qui permet de calculer la hauteur d’une pyramide à partir de l’apothème directement. Par contre, on utilise une formule très répandue dans le domaine des mathématiques : le théorème de Pythagore.
Trouver la mesure de la hauteur à partir de l’apothème
Dans le cas d'une pyramide droite, on peut obtenir un triangle rectangle en traçant la hauteur issue de l'apex et en rejoignant le centre de la base. Cette hauteur s’appelle l’apothème de la pyramide.
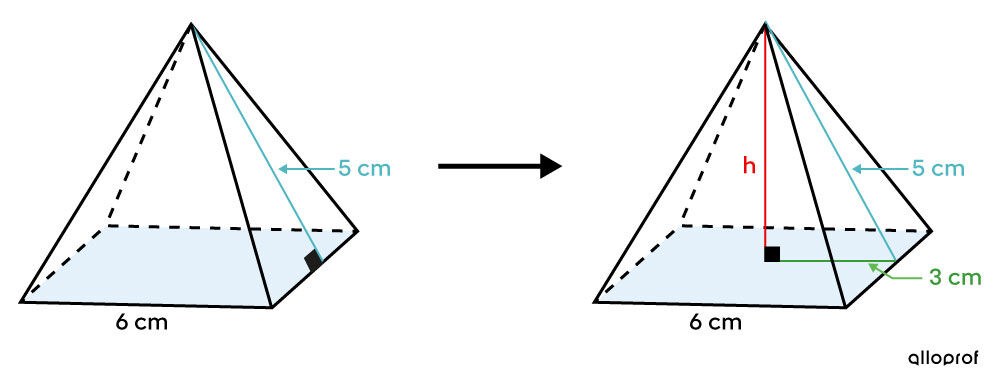
Puisque la hauteur de la pyramide se termine au centre de sa base et que c'est une pyramide droite, la mesure de la cathète correspond à la moitié de la mesure du côté de la base.
En associant la mesure d'une cathète avec la moitié de celle d'un côté de la base, l'autre cathète avec celle de la hauteur de la pyramide et l'apothème avec celle de l'hypoténuse, on peut utiliser le théorème de Pythagore : ||\begin{align} \color{#3A9A38}{a}^2 + \color{#EC0000}{b}^2 &= \color{#51B6C2}{c}^2\\\\ \color{#3A9A38}{3}^2 + \color{#EC0000}{h}^2 &= \color{#51B6C2}{5}^2\\ \color{#EC0000}{h}^2 &= 16\\ \color{#EC0000}{h} &= 4 \ \text{cm}\end{align}||
Si tu cherches la mesure de l’apothème à partir de la hauteur, c’est encore le théorème de Pythagore qu’il faut utiliser.
Vidéo
Le volume des pyramides et des cônes
Moments dans la vidéo :
- 00:00-La formule du volume
- 01:28-Exemple avec une pyramide
- 02:24-Exemple avec un cône