Matières
Niveaux
Les mesures manquantes des solides à partir du volume
Fiche | Mathématiques
Secondaire
3
Table des matières
- Haut de page
- Trouver la mesure manquante d'un cube
- Trouver une mesure manquante d'un prisme
- Trouver une mesure manquante d'un cylindre
- Trouver une mesure manquante d'une boule
- Trouver une mesure manquante d'une pyramide
- Trouver une mesure manquante d'un cône
- Trouver la mesure de l’apothème d'une pyramide ou d'un cône
- À voir aussi
- Exercice
Dans certains problèmes, il arrive que l'on connaisse le volume d'un solide ainsi que toutes ses mesures, sauf une. Il faut donc savoir trouver une mesure manquante.
La procédure à suivre pour trouver une mesure manquante dans un solide est généralement la même peu importe son type. Voici les principales étapes.
-
Identifier les mesures données.
-
Déterminer la formule à utiliser.
-
Remplacer les variables par les mesures données.
-
Isoler la variable recherchée.
Trouver la mesure manquante d'un cube
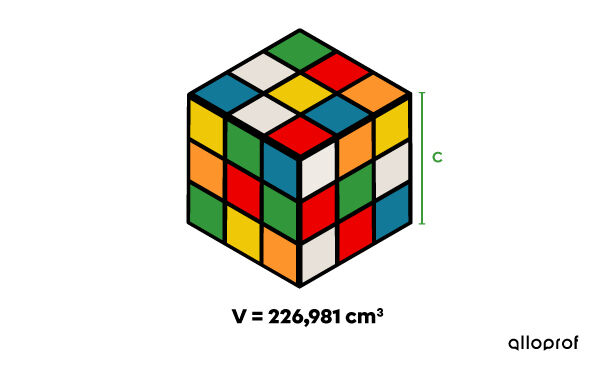
Afin de passer le temps durant les pauses à ton école, tu gardes toujours un Cube Rubik dans ton sac à dos. Or, avec tout ce que tu dois mettre dans ton sac, il te reste un espace disponible de seulement 226,981 cm3.
Quelle devrait être la mesure maximale des arêtes du Cube Rubik afin que tu puisses le ranger dans ton sac à dos?
Voir la solution
Trouver une mesure manquante d'un prisme
En tant que camionneur, Bobby doit s'assurer que les routes qu'il emprunte sont suffisamment dégagées en hauteur afin de ne pas abimer son camion et la marchandise qu'il transporte. Alors qu’il est sur la route pour sa prochaine livraison, il aperçoit le panneau suivant.
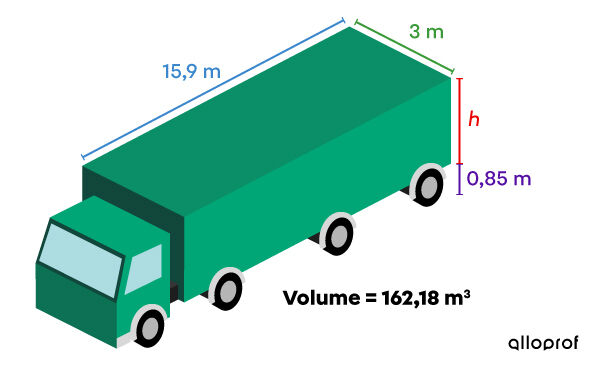
Connaissant seulement le volume de la section d'entreposage de son camion, Bobby s'arrête sur le bord de la route afin de vérifier que son camion n'est pas trop haut pour passer sous la prochaine passerelle.
Comme il lui est impossible d'atteindre le dessus de son camion, quels calculs doit-il faire pour déterminer la hauteur de son véhicule?
Voir la solution
Trouver une mesure manquante d'un cylindre
Afin d'assurer l'efficacité des divers filtres à air, les usines de production doivent s'assurer que leurs cheminées ne contiennent pas plus de 385 m3 de déchets gazeux.
En se fiant aux plans de la bâtisse ci-dessus, quelle devrait être la hauteur minimale de la cheminée de forme cylindrique?
Voir la solution
Trouver une mesure manquante d'une boule
Pour prendre part à une partie de Bubble soccer, il faut revêtir un équipement assez particulier. En fait, les joueurs doivent porter une énorme bulle de protection sphérique qui leur permet d'entrer sécuritairement en contact avec les autres joueurs.
Le seul inconvénient est que les participants doivent être au moins aussi grands que la hauteur de cette bulle de protection. Sachant que le volume d'une bulle protectrice est de 1,44 m3, quelle doit être la taille minimale des participants?
Voir la solution
Trouver une mesure manquante d'une pyramide
Sachant qu’il a fallu 2 592 341 m3 de pierre pour bâtir la pyramide de Khéops en Égypte et qu’il s’agit d’une pyramide régulière à base carrée de 230 m de côté, quelle est la hauteur de la pyramide?
La pyramide de Khéops
Source : kallerna, wikipedia.org
Voir la solution
Trouver une mesure manquante d'un cône
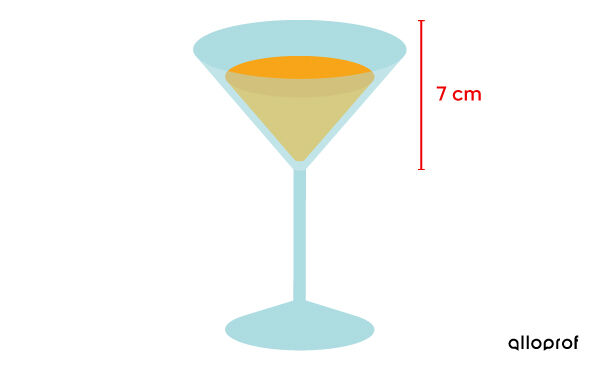
Afin de s'assurer de faire un bon profit, un propriétaire de restaurant veut déterminer le diamètre exact que devraient avoir les verres dans lesquels les boissons seront servies.
De façon générale, une consommation équivaut à 90 mL, soit 90 cm3. Si cette quantité est respectée, quel est le diamètre nécessaire des verres en considérant que l'épaisseur du verre est négligeable?
Voir la solution
Pour la pyramide comme pour le cône, il arrive parfois qu’on doive déterminer la mesure de l’apothème du solide à partir du volume alors que cette mesure ne se retrouve pas dans la formule du volume. Dans ces cas, il faut d’abord trouver la hauteur du solide ou le rayon de la base. Ensuite, il faut faire une étape supplémentaire, soit calculer la mesure de l’apothème à l’aide du théorème de Pythagore.
Trouver la mesure de l’apothème d'une pyramide ou d'un cône
Comme il faut effectuer sensiblement la même démarche pour trouver la mesure de l'apothème d’un cône ou d’une pyramide, seul le cône est présenté dans l’exemple qui suit.
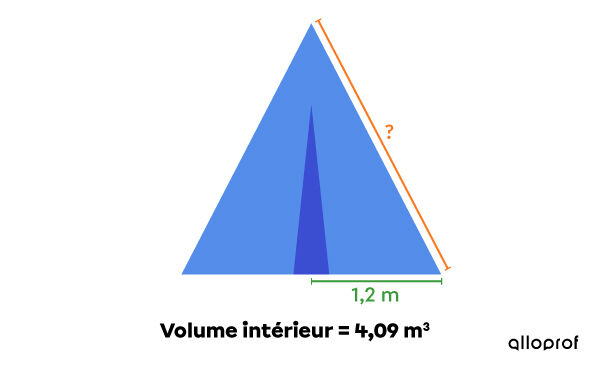
Pour éviter qu'une tente de forme conique soit emportée par le vent, on fixe des cordes qui relient son apex au sol à l’aide de pieux. Ces cordes de sécurité doivent longer les parois de la tente.
En tenant compte des renseignements présents sur la figure et sachant qu'il faut prévoir 30 cm additionnels aux deux extrémités de chaque corde pour faire un nœud, quelle est la longueur minimale d'une de ces cordes?
Voir la solution
Comme on peut le voir dans l’exemple précédent, il faut trouver la mesure de la hauteur avant de déduire celle de l'apothème à l'aide du théorème de Pythagore. Autrement dit, trouver la mesure de l'apothème d’un cône ou d’une pyramide à partir du volume exige quelques calculs de plus que ceux pour trouver la hauteur.
Si, au lieu du volume, on connait l’aire latérale d’un cône ou d’une pyramide ainsi que les dimensions de sa base, on peut alors trouver la mesure de l’apothème directement. En effet, on retrouve bel et bien cette mesure dans la formule de l’aire latérale des cônes et des pyramides. La formule de l’aire latérale de ces solides est |A_L = \dfrac{P_b \times a}{2}.|
S’il faut trouver la hauteur d’un de ces solides à partir de l’aire latérale, il faut donc commencer par trouver la mesure de l’apothème. Puis, en utilisant le théorème de Pythagore, on trouve la hauteur. Pour voir un exemple, consulte la fiche Trouver la mesure de la hauteur d’une pyramide ou d’un cône.
Pour valider ta compréhension à propos des mesures manquantes dans les solides de façon interactive, consulte la MiniRécup suivante.
