Matières
Niveaux
Le rapport trigonométrique sinus
Fiche | Mathématiques
Secondaire
4
Table des matières
- Haut de page
- Trouver la mesure d'un côté à l’aide du rapport trigonométrique |\boldsymbol\sin|
- Trouver la mesure d’une cathète à l’aide du rapport |\boldsymbol\sin|
- Trouver la mesure de l’hypoténuse à l’aide du rapport |\boldsymbol\sin|
- Astuce
- Trouver la mesure d'un angle à l’aide de |\boldsymbol{\sin^{-1}}|
- À voir aussi
Le rapport sinus est l’un des 3 principaux rapports trigonométriques que l'on retrouve dans un triangle rectangle.
Dans un triangle rectangle, le sinus d’un angle |(\boldsymbol \theta)| correspond au rapport entre la mesure de la cathète opposée à l’angle et la mesure de l’hypoténuse.||\sin \theta=\dfrac{\text{cathète $\color{#EC0000}{\text{opposée}}$ à l'angle }\theta}{\text{$\color{#3A9A38}{\text{hypoténuse}}$}}||
Ainsi, si on veut déterminer le sinus des angles aigus dans le triangle rectangle suivant, on obtient 2 rapports.
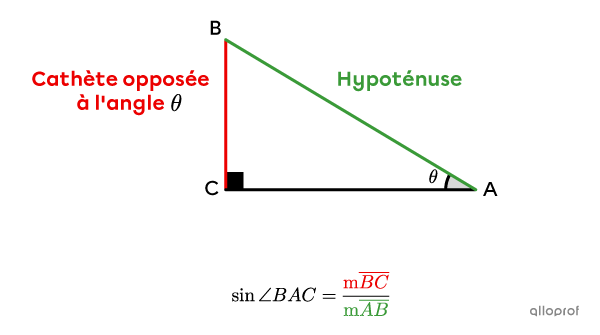
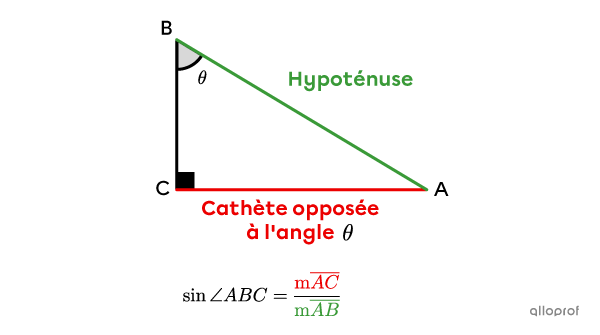
Le rapport trigonométrique sinus ne s’utilise qu’avec les angles aigus d’un triangle rectangle. Ainsi, on ne cherche jamais le sinus à partir de l’angle droit.
Trouver la mesure d'un côté à l’aide du rapport trigonométrique |\boldsymbol\sin|
Trouver la mesure d’une cathète à l’aide du rapport |\boldsymbol\sin|
Pour déterminer la mesure d’une cathète dans un triangle rectangle à l’aide du rapport sinus, on doit connaitre la mesure de l’hypoténuse et celle de l’angle opposé au côté recherché.
Détermine la mesure du côté |\overline{BC}| à l’aide du rapport sinus dans le triangle rectangle suivant.
Voir la solution
Pour plus de précision, il est préférable d’effectuer le calcul en une seule étape sur la calculatrice. Si ce n’est pas possible, il est avantageux de conserver un minimum de 3 à 4 chiffres après la virgule.
Voici un exemple lorsque |\theta=65^{\circ}| et que l’hypoténuse mesure |59\ \text{cm}.|
En effectuant le calcul en 1 seule étape
|\begin{align}\sin65^{\circ}&=\dfrac{a}{{59}}\\\sin65^{\circ}\times59&=a\\\color{#EC0000}{53{,}47}&\approx a\end{align}|
En effectuant le calcul en 2 étapes
|\begin{align}\sin65^{\circ}&=\dfrac{a}{59}\\\color{#ec0000}{0{,}91}&\approx\dfrac{a}{59}\\0{,}91\times59&\approx a\\\color{#EC0000}{53{,}69}&\approx a\end{align}|
En effectuant le calcul en 2 étapes et en ne conservant que 2 décimales lors du calcul du sinus de l’angle, on obtient une différence de 22 centièmes avec la réponse attendue.
Dans certains cas, ni la mesure du côté opposé à l’angle ni celle de l'hypoténuse sont connues. Pour pouvoir appliquer le rapport sinus, il faut alors déterminer la mesure de l’autre angle.
Détermine la mesure de la cathète recherchée à l’aide du rapport sinus dans le triangle rectangle suivant.
Voir la solution
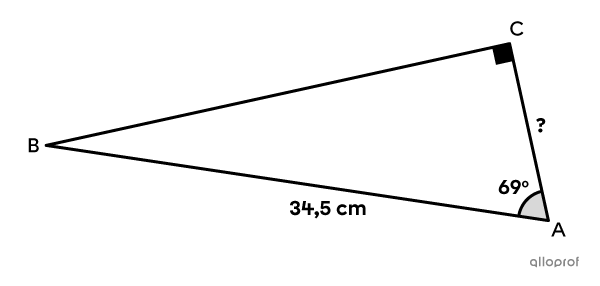
Dans l’exemple précédent, il aurait été possible d’utiliser le rapport trigonométrique cosinus pour déterminer la mesure de la cathète recherchée à l’aide de l’angle de |69^{\circ}.| La réponse aurait alors été la même.
Trouver la mesure de l’hypoténuse à l’aide du rapport |\boldsymbol\sin|
Pour déterminer la mesure de l’hypoténuse dans un triangle rectangle à l’aide du rapport sinus, on doit connaitre la mesure d’un angle aigu et celle de son côté opposé.
Détermine la mesure de l’hypoténuse à l’aide du rapport sinus dans le triangle rectangle suivant.
Voir la solution
Le rapport sinus avec un angle de |\boldsymbol{30^{\circ}}|
Dans un triangle rectangle, la mesure de la cathète opposée à l'angle de |30^{\circ}| est toujours égale à la moitié de celle de l'hypoténuse.
Le rapport sinus est donc toujours de |\dfrac{1}{2}.|||\begin{align}\sin30^{\circ}&=\dfrac{\text{cathète $\color{#EC0000}{\text{opposée}}$ à l'angle }\theta}{\text{$\color{#3A9A38}{\text{hypoténuse}}$}}\\&=\dfrac{\frac{\color{#3A9A38}c}{2}}{\color{#3A9A38}c}\\&=\dfrac{1}{2}\end{align}||
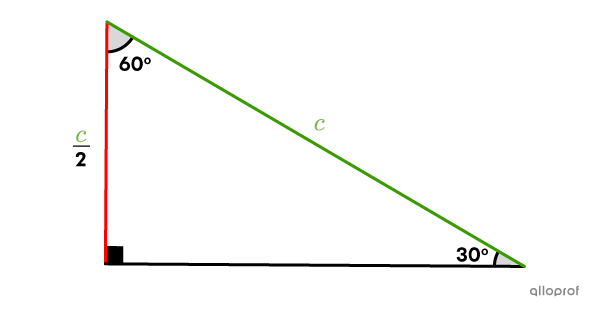
Quelle est la mesure du côté |\overline{AB}| dans le triangle suivant?
Voir la solution
Trouver la mesure d'un angle à l’aide de |\boldsymbol{\sin^{-1}}|
Pour déterminer la mesure d’un angle aigu dans un triangle rectangle à l’aide du rapport sinus, on doit connaitre la mesure de son côté opposé et celle de l’hypoténuse. Cela revient à répondre à la question suivante : « Quel angle me donne un sinus de…? »
On détermine d’abord le rapport sinus, puis on utilise la touche |\sin^{-1}| (qu’on appelle aussi |arcsin|) sur la calculatrice.
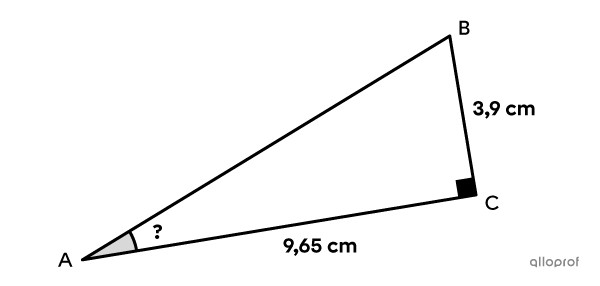
Détermine la mesure de l’angle |BAC| dans le triangle rectangle suivant à l’aide du rapport sinus.
Voir la solution
En trigonométrie, plusieurs démarches sont possibles pour arriver au même résultat. Dans l’exemple précédent, on aurait pu utiliser |\boldsymbol{\tan^{-1}}| à partir de l’angle |BAC,| ce qui aurait donné sa mesure.
La fonction arc sinus, notée |\sin^{-1}(x),| est la réciproque de la fonction sinus.||\sin \theta=x\ \Leftrightarrow \ \sin^{-1}x=\theta||
À voir aussi
- Les rapports trigonométriques dans le triangle rectangle
- Le rapport trigonométrique cosinus
- Le rapport trigonométrique tangente
- Les relations métriques dans le triangle rectangle
- La loi des sinus
- La loi des cosinus
- L'aire des triangles à l'aide de la trigonométrie
- L'aire des triangles à l'aide de la formule de Héron