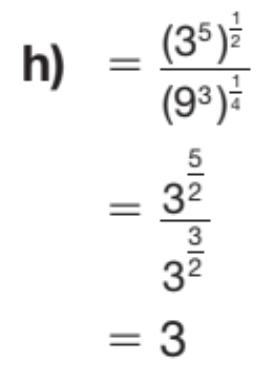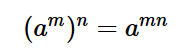Best Of
Re: Question
Salut!
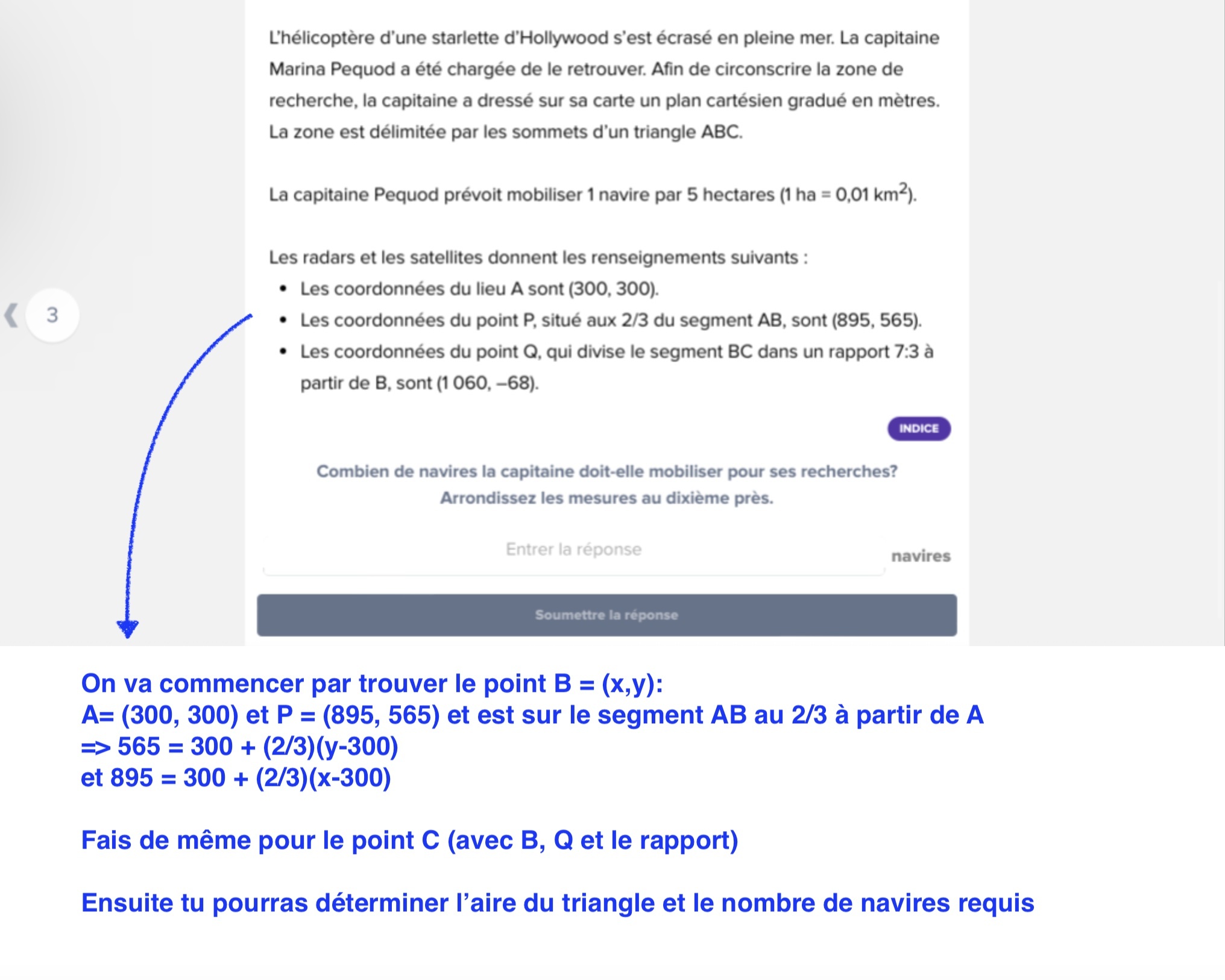
(895, 565) sont les coordonnées du point P.
On te dit que le point P est situé au 2/3 du segment AB. Nous n'avons pas besoin du point P spécifiquement. Par contre, cette information nous permet de calculer les coordonnées du point B!
Le point P est le point de partage du segment AB. On peut donc utiliser cette formule pour trouver les coordonnées de la 2e extrémité du segment, soit le point B :
De plus, (1060, -68) sont les coordonnées du point Q. Tout comme le point P, le point Q est un point de partage qui nous sert uniquement à trouver les coordonnées d'un autre point. On sait qu'il divise le segment BC dans un rapport 7/3. Ainsi, on peut trouver les coordonnées du point C en appliquant la formule mentionnée précédemment.
J'espère que c'est plus clair pour toi! :)
Re: Question
Bonsoir à toi,
Tout comme PerleTimide l'a dit, il y a environ 8000 verbes en français. Les verbes les plus fréquents ne représentent que 2000 verbes maximum. Les autres sont d'un usage plus rare. Il y a 500 verbes les plus fréquents qui représentent 95% des demandes de verbe. Voilà, j’espère que cela répond bien à ta question. Merci d’avoir pris le temps de nous écrire.
Marie-Eve
Re: Question
Pour te pratiquer pour des examens de lecture, c’est de te pratiquer en formulant des phrases claires et de surtout donner des exemples provenants du texte! Bonne réussite!
Question
Bonne soirer alloprof,
Se calcul ne fais pas de sens n'ait-ce pas? La vrai réponse est 3 exposant 5/3?
Merci!
Re: Question
Salut!
Ce calcul est correct!
On commence par multiplier les exposants selon cette loi des exposants :
Ce qui nous donne ceci :
$$\frac{(3^5)^{\frac{1}{2}}}{(9^3)^{\frac{1}{4}}}$$
$$=\frac{(3)^{\frac{1\times 5}{2}}}{(9)^{\frac{1 \times 3}{4}}}$$
$$=\frac{(3)^{\frac{5}{2}}}{(9)^{\frac{3}{4}}}$$
Puis, on peut remplacer 9 par 3² :
$$=\frac{(3)^{\frac{5}{2}}}{(3^2)^{\frac{3}{4}}}$$
Et on applique de nouveau la même loi utilisée précédemment :
$$=\frac{(3)^{\frac{5}{2}}}{(3)^{\frac{3\times 2}{4}}}$$
$$=\frac{(3)^{\frac{5}{2}}}{(3)^{\frac{6}{4}}}$$
On réduit la fraction 6/4 :
$$=\frac{(3)^{\frac{5}{2}}}{(3)^{\frac{3}{2}}}$$
Finalement, on applique cette loi des exposants :
$$=3^{\frac{5}{2} -\frac{3}{2}}$$
$$=3^{\frac{5-3}{2} }$$
$$=3^{\frac{2}{2} }$$
$$=3^{1 }$$
$$=3$$
Voilà! J'espère que c'est plus clair pour toi! :)
Re: Question
Bonsoir AigleOrange6934, merci pour ta question !
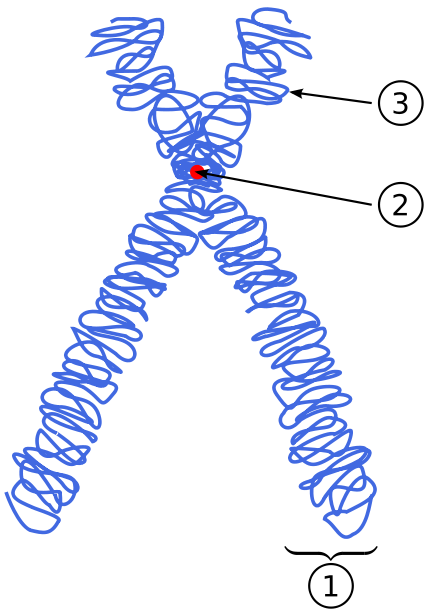
En fait ADN et chromosome servent à nommer la même chose. Les chromosomes sont des brins d'ADN qui sont enroulés sur eux-mêmes. Donc un chromosome, c'est de l'ADN condensée pour qu'il soit plus facilement déplaçable pendant la mitose et la méiose.
Voici un schéma qui représente un chromosome, en bleu, ce sont les deux brins d'ADN du chromosome :
Si tu veux en savoir plus je t'invite à aller voir la fiche suivante : https://www.alloprof.qc.ca/fr/eleves/bv/sciences/l-adn-les-genes-et-les-chromosomes-s1227
N'hésite pas à nous écrire si tu as d'autres questions !
Question
a l école sa se pase mal je peux pas fair bien la siense
et on se moque de moi
Re: Question
Bonjour BaryumRose9419, merci pour ta question !
Oui, tu as bien raison ! La molécule Cs3N se nomme nitrure de tricésium. Le préfixe "tri-" indique qu'il y a trois atomes de césium pour un atome d'azote dans cette molécule.
C'est une nomenclature correcte pour indiquer la composition chimique de la molécule.
Si tu as d'autres questions, n'hésite pas à nous réécrire !
Re: Question
Bonsoir! :) Merci de faire appel à nos services! :D
Voici les incontournables pour bien planifier son étude selon moi. Tu peux cliquer sur les hyperliens en bleu pour accéder aux articles à propos de chaque sujet! :D
- Avoir un agenda ou un outil de planification (on en a un à imprimer juste ici)
- Réserver du temps sans distraction pour étudier (tu peux te servir de notre minuterie motivante!)
- Avoir une bonne hygiène de vie et adapter son plan d'études en fonction de ses capacités de concentration
Voici d'autres trucs :
https://www.alloprof.qc.ca/fr/parents/articles/aide-devoirs/strategies-mieux-sorganiser-ecole-k1230
https://www.alloprof.qc.ca/fr/parents/articles/aide-devoirs/planifier-devoirs-secondaire-k1228
Tu peux consulter notre section Examen et trucs d'étude pour en avoir plus! N'hésite pas à aussi effectuer des recherches par mots-clés pour trouver des fiches plus précises (ex Trucs pour répondre à des questions de lecture, Trucs pour étudier en histoire).
Si tu as des questions en lien avec la matière, n'hésite pas! :D
Sarah G