Best Of
Re: Question
Salut CaramboleTurquoise3629! 😎
1 : Oui, les cégeps vont regarder chaque matière et elles vont compter dans ta moyenne générale. Les notes vont être pondérés avec tes notes d'examen du ministère. La pondération va dépendre de l'écart entre tes deux notes.
2 : Pour connaitre la note qu'il te faut, tu peux regarder les notes minimales qui ont été acceptées lors des dernières années. tu ne peux pas connaitre la note exacte puisque ça va dépendre des demandes d'Admissions que le cégep va recevoir. Pour le 60%, c'est plus comme un prérequis, comme certains cours selon le programme. Certains programmes ont assez de place pour chaque demande, alors il faut simplement que tu passes chaque cours pour être accepté.
3 : Non, les cégeps ne regardent pas chaque étape séparément, comme la 2e étape par exemple. Ce qui compte, ce sont les notes finales (la moyenne de toutes les étapes + la note de l’examen du ministère s’il y en a un).
J’espère que la réponse t’a aidé! Ne te gêne pas si tu as d’autres questions, ça va me faire plaisir d’y répondre! 😊
PoutineOrange5768
Re: Question
salut! Je suis dans la meme situation, je fais tous les exercices que je peux mais je comprends même pas la moitié de mes exercices ! Je te conseillerais de poser le plus de questions possibles à ton ou ta prof et fais le plus d’exercice possible, c’est ça qui aide en math de sec 4. Bonne chance et tu n’est pas la seule ou le seul à être mélangé comme ça!
Re: Question
Salut !
Selon les équations que tu as trouvé, il semble en effet que ton polygone soit correctement hachuré !
Il ne te reste plus qu'à trouver les coordonnées des sommets de ce polygone est de déterminer lequel optimise la situation !
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne soirée !
Re: Question
Salut!
Voici des exercices qui pourraient t'intéresser :
Voici également une fiche qui pourrait t'être utile :
Bonne pratique! :)
Re: Question
Salut!
Non, ce n'est pas la bonne réponse. Regardons ensemble comment débuter cette factorisation :)
$$16x^2-25(x+2)^2$$
On ne peut pas appliquer la différence de carrés tout de suite, puisque les deux termes ne sont pas des carrés! Présentement, l'exposant 2 est appliqué à un seul facteur du terme, et non le terme au complet. Donc, il faut réécrire 16 et 25 afin qu'ils fassent partie du carré :
$$(4x)^2-(5(x+2))^2$$
On est maintenant prêts à appliquer la différence de carrés!
$$[(4x)-(5(x+2))][(4x)+(5(x+2))]$$
On peut éliminer les parenthèses inutiles :
$$[4x-5(x+2)][4x+5(x+2)]$$
Il faut maintenant distribuer les multiplications sur les parenthèses, puis simplifier l'expression.
Je te laisse terminer. J'espère que cela t'aide! :)
Question
J’ai de la misère avec ce problème, je sais que la formule est v1/v2= racine carré M2/M1, mais je ne comprends pas comment le faire
Re: Question
Salut !
Comme il s'agit de proportions, tu peux utiliser le produit croisé (règle de trois).
Par exemple, pour convertir, la première étape est d'avoir les bonnes unités. Ainsi, \(78cmHg=780mmHg\). À partir de là, tu peux effectuer le produit croisé.
$$ \frac{780mmHg}{760mmHg}=\frac{?}{1atm} $$
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne soirée !
Re: Question
Salut !
Essayons de comprendre la situation ensemble. Il y a une quantité initiale dans la piscine (\(V_{initial}\). Puis, on vide d'un volume de \(6a+2b-8\) et on ajoute \(a-6\). Cela donne un volume final de \(89a+108b+225\) et on veut l'expression de (\(V_{initial}\). Cela donne donc l'équation suivante à résoudre.
$$ V_{initial}-(6a+2b-8)+(a-6)=(89a+108b+225) $$
$$ V_{initial}=(89a+108b+225)+(6a+2b-8)-(a-6) $$
Il s'agit là de l'équation qui te donnera une expression algébrique pour (\(V_{initial}\). J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne soirée !
Re: Question
Salut !
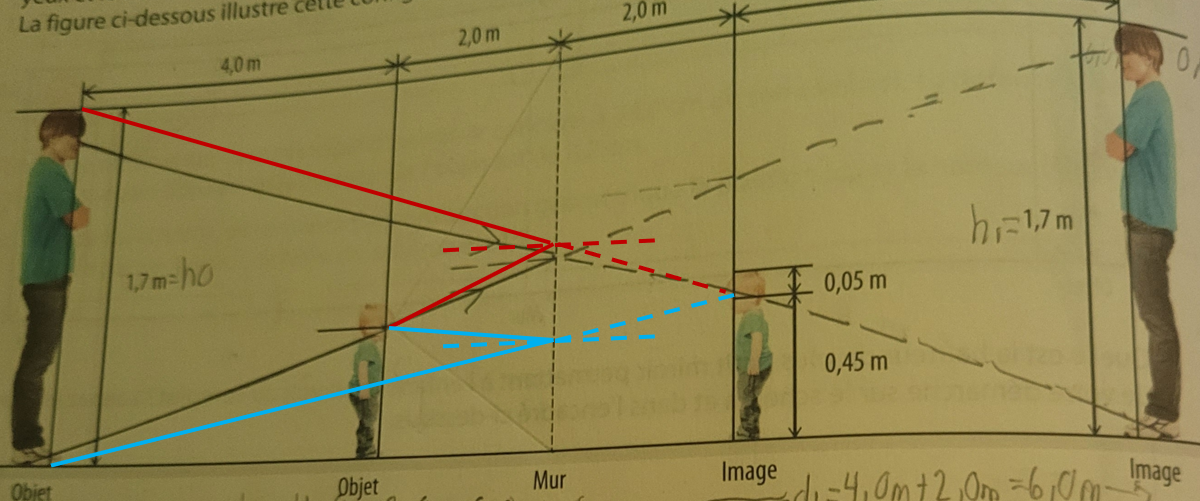
Pour que l'enfant (réel) puisse voir tout le corps de l'homme (image), il faut que l'enfant (image) puisse voir tout le corps de l'homme (réel). Donc, les rayons peuvent partir des yeux de l'enfant pour rejoindre les deux extrémités de la hauteur de l'homme comme suit :
Tu peux ainsi voir les deux extrémités minimales du miroir. Le reste est une question de géométrie.
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne soirée !