Best Of
Re: Question
Bonjour PommeEnthousiaste328
pour t'aider tu peux prendre du carton ou du papier comme tu veux. Tu écries toutes tes table de multiplication sur un bout de papier différent pour chaque multiplication. Ensuite, quand tu a fini tu les mélanges. tu ais une seul pile et tu prend un carton. tu essais de la faire en bas de 5 seconde si tu y arrive met le dans une autre pile et si tu n'y arrive pas remet le en dessous de ta pile de toute tes multiplication.
(oublie pas de mettre les réponse en arrière du carton ou la feuille pour te corriger de suite pour ne pas faire d'erreur prend une calculatrice pour mettre les réponses au dos de la fiche )
DragonFormidable6604
Question
Bonjour je n’arrive pas à résoudre ce problème , j’ai esseyer par identite trigonométrie avec un triangle et pytagore, mais sa na pas marcher
Re: Question
Bonsoir DauphinExemplaire6085!
Merci beaucoup pour ta question!
Pour parvenir à résoudre ton problème tu dois utiliser la méthode de produit croisé.
Tu dois premièrement trouver le nombre total d'élève en première secondaire. Pour y arriver, tu sais que les garçons représentent 2/5 pour un nombre de 66. Donc 66 sur le nombre total d'élève en première secondaire. Quand tu auras le nombre total d'élèves de première secondaire tu pourras soustraire le nombre de garçons (66) pour obtenir le nombre de filles.
Pour le B), tu utiliseras le nombre d'élèves qui sont en première secondaire que tu as obtenu au A) pour déterminer combien d'élèves il y a au total dans l'école si ceux de première secondaire représentent le 1 sixième (1/6).
En espérant que ma réponse ait pu t’aider et n’hésite pas à nous réécrire si des questions persistent.
Bonne soirée!
Re: Question
Salut!
En effet, il se peut très bien que le graphique ne soit pas à l'échelle, il ne faut donc pas se fier à cela pour déduire des informations.
Cependant, il n'est en fait pas important de déterminer quel segment est le plus grand. Le 3/2 est un rapport, cela ne signifie pas qu'un des segments a la partie 2 et l'autre le 3!
Ce rapport te servira uniquement à trouver les coordonnées du point de partage à l'aide de la formule suivante :
La première extrémité sera le point de départ (0 ; 5,6), et la 2e extrémité sera le point d'arrivée du déplacement, soit le point (? ; 15,2).
Voici une fiche sur cette notion qui pourrait t'être utile : Le point de partage et le point milieu d'un segment | Secondaire | Alloprof
Si tu as d'autres questions, on est là! :)
Re: Question
Bonjour DauphinExemplaire6085,
Merci d'avoir utilisé la zone d'entraide pour répondre à ta question!
Tout d'abord, 2/5 est égale à 4/10. 1/2 est égale à 5/10. Au total, il a vendu 9/10 du nombre de pains à l'ouverture du magasin. 10/10 - 9/10 = 1/10, alors 1/10 est égale à 12 pains. Sachant cela, tu peux trouver le nombre de pains initial.
Pour t'aider plus, je te suggère de consulter cette fiche:
J'espère que j'ai pu t'aider à répondre à ta question,
Ne lâchez pas,
SourisRapide3938
Re: Question
@alloprof
Je crois qu il faut utiliser l identité fondamentale en trigonométrie (et non la fonction inverse) pour calculer les valeurs exactes des rapports.
On trouve cos(x) = -21/29.
Re: Question
Bonjour DodoJaune1817,
Nous te remercions de nous avoir écrit!
Dans un grahique:
A, c'est l'hauteur entre les lignes
B, c'est 1/la longueur d'une ligne
H, c'est le point fermé le plus proche de 0 sur l'axe des x
K, c'est le point fermé le plus proche de 0 sur l'axe des y
Voici une exemple:
N'hésite pas à nous réécrire si tu as d'autres questions et nous t'aiderons avec plaisir!
-QuartzFormidable8241
Re: Question
Salut!
On souhaite pouvoir rembourser le 400$ grâce à l'argent amassé par la vente de billet. Donc, on a l'équation suivante :
Nombre de billets vendus × prix d'un billet = 400$
Si nous posons x (variable indépendante) comme étant notre nombre de billets vendus et y (variable dépendante) comme étant le prix d'un billet, on a l'équation :
$$ x \times y = 400$$
$$ y = \frac{400}{x} $$
Nous avons donc une fonction rationnelle! Il ne te reste plus qu'à calculer y si x=115 pour répondre à la seconde question.
J'espère que c'est plus clair pour toi! :)
Question
Bonjour Mme Katia K. Merci beaucoup pour votre aide sur les différentes formes d'équation de la droite. Merci aussi à FerUpsilon de m'avoir aidé...
Pouvez-vous m'aidez davantage Madame s.v.p??
J'ai beaucoup de difficultés en algèbre. Je pratique, pratique et pratique, mais j'ai toujours des questions stupides qui me bloquent. Je sais plus quoi faire et je me sens stupide...
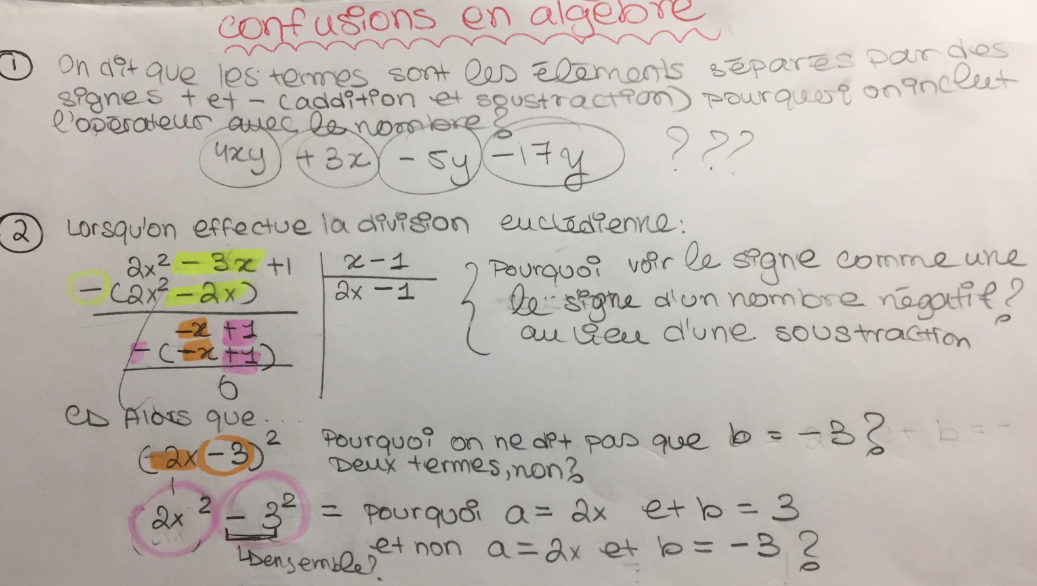
1) Lorsqu'on parle des termes, j'en comprends rien! En fait, je ne comprends pas comment le signe de soustraction peut indiquer qu'un nombre est négatif.
Si j'ai 10x - 8x, c'est une soustraction, non? Je ne comprends pas pourquoi on les voit comme une série de nombres en le collant avec les signes(10x est un nombre et -8x est un nombre???? Alors d'où vient la soustraction??) Est-ce que je vois le tout comme 3 éléments distincts (10x et - et 8x) ou (10x et -8x)?
2) Je vous ai inséré une photo qui englobe certains cas où je me doute si il faut prendre le moins avec le nombre ou pas... ( on peut dire 10x - (+8x) ou 10x +(-8x), mais lequel choisir?? )
J'ai beaucoup de difficultés, s.v.p aidez-moi :(
Désolée pour mes questions bizarres.
Merci...
Re: Question
Salut!
Merci pour ta question! :)
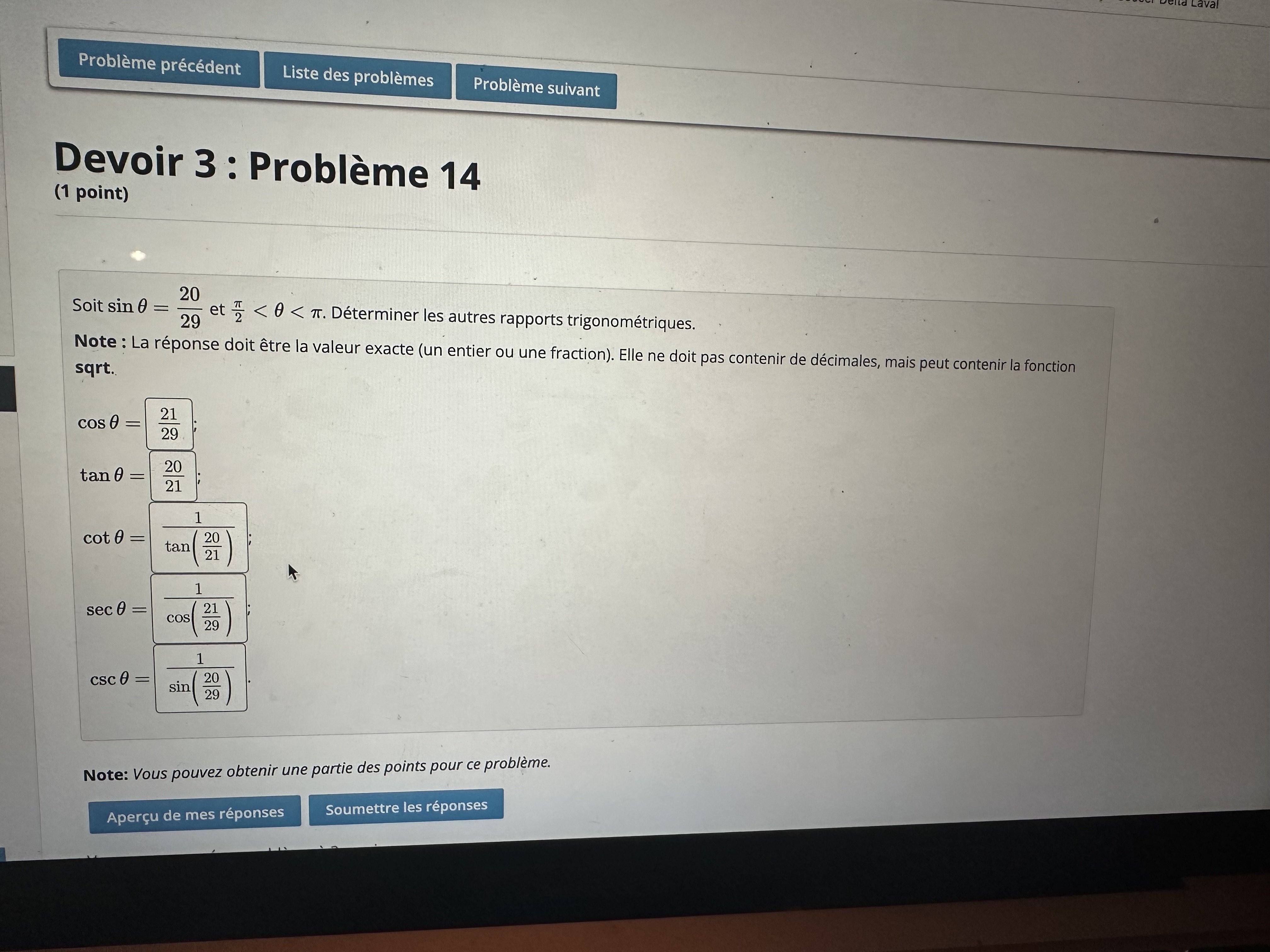
On te dit que le sinus d'un certain angle est de \(\frac{20}{29}\), et que cet angle est entre \(\frac{π}{2}\) et \(π\).
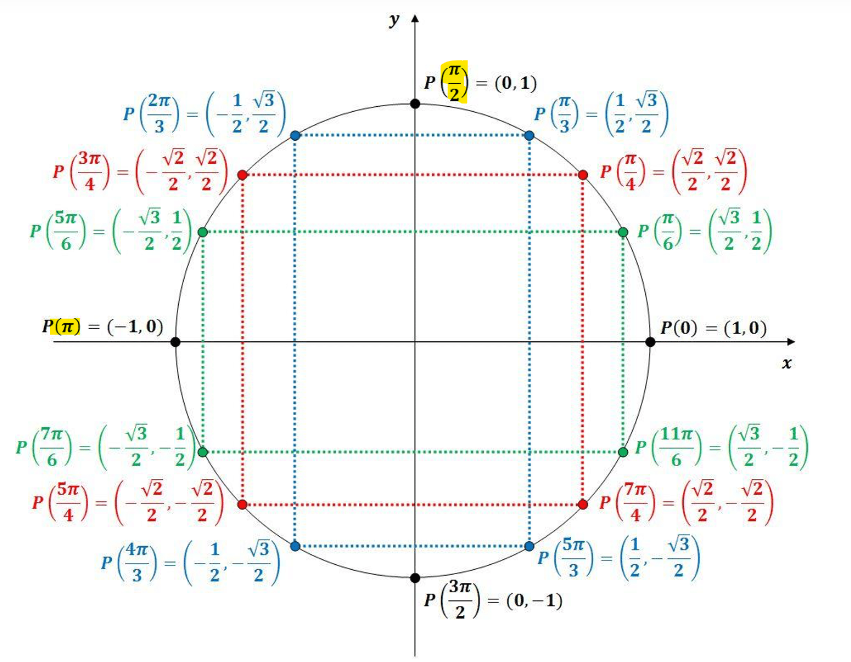
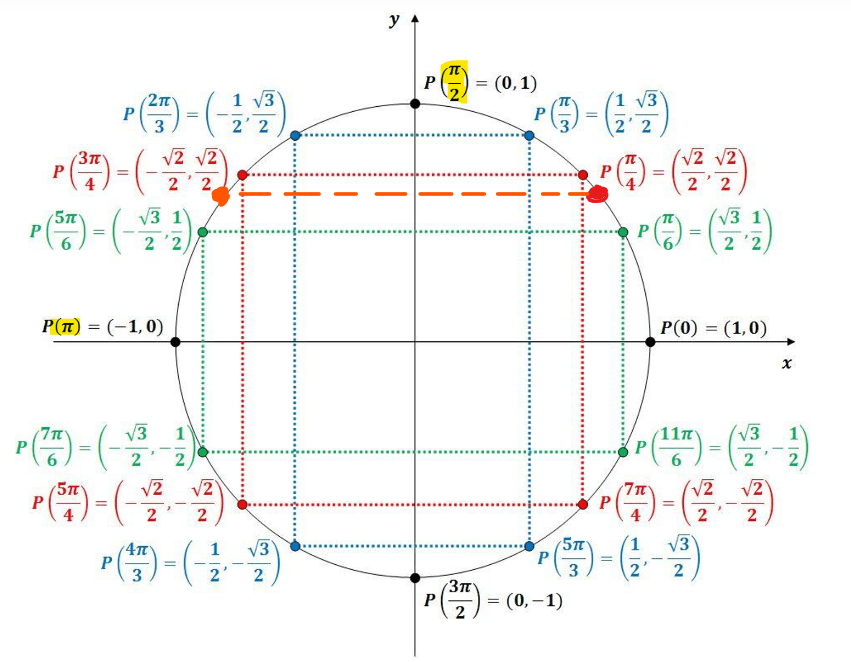
À l'aide de notre cercle trigonométrique, on constate alors que l'angle est entre 90° (\(\frac{π}{2}\) rad) et 180° (\(π\) rad) :
Tu peux trouver l'angle principal dans le premier quadrant ayant un sinus de 20/29 en résolvant l'équation donnée :
$$ sinθ = \frac{20}{29} $$
$$ θ = sin^{-1}(\frac{20}{29} ) = 0,761 ~rad$$
On trouve ainsi que l'angle 0,761 rad possède un sinus de 20/29. En d'autres mots, la coordonnée en y de l'angle 0,761 rad est de 20/29 dans le cercle trigonométrique.
Cependant, cet angle n'est pas dans l'intervalle souhaité, puisqu'on veut être entre 1,57 rad (\(\frac{π}{2}\) rad ≈ 1,57 rad) et 3,15 rad (\(π\) rad ≈ 3,15 rad), on veut être dans le 2e quadrant, et non le premier! L'angle de 0,761 rad est environ ici :
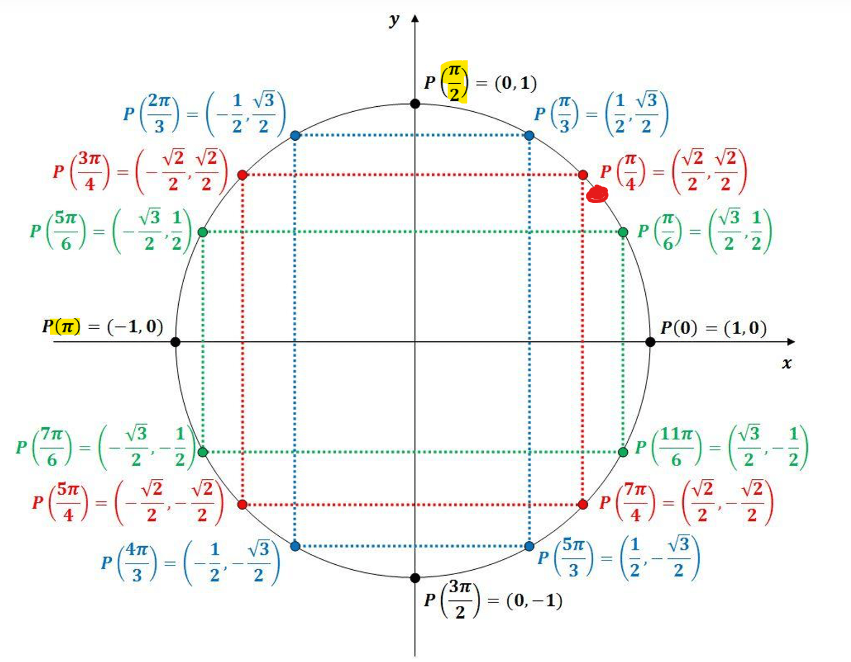
On veut donc trouver son équivalence dans l'intervalle désiré :
Nous cherchons donc l'angle du point orange qui possède aussi une coordonnée en y de 20/29 (si nous avions eu cos au lieu de sin dans l'équation, on serait aller vers le bas du cercle, puisqu'on veut avoir la même coordonnée en x).
Pour aller de l'angle rouge de 0,761 rad à l'angle orange, tu dois trouver le complément de 0,761 rad dans le second quadrant en soustrayant cet angle de pi :
$$ \pi - 0,761 = 2,381 rad $$
L'angle ayant un sinus de 20/29 et se situant entre \(\frac{\pi}{2}\) et \(\pi\) est donc 2,381 rad.
Il ne te reste plus qu'à utiliser ta calculatrice pour trouver le cos, tan, cot, sec et csc de cet angle.
J'espère que c'est plus clair pour toi! :)