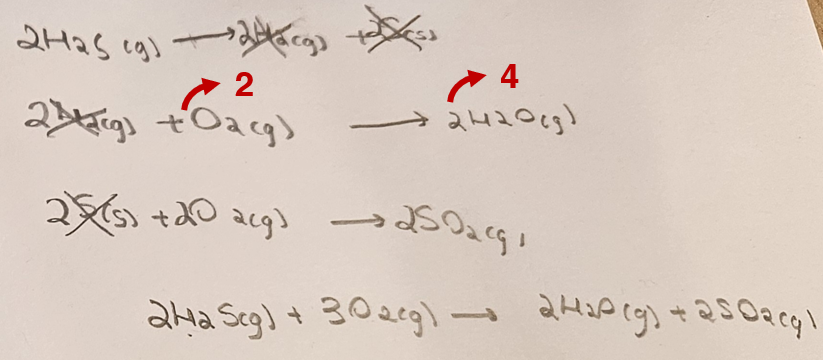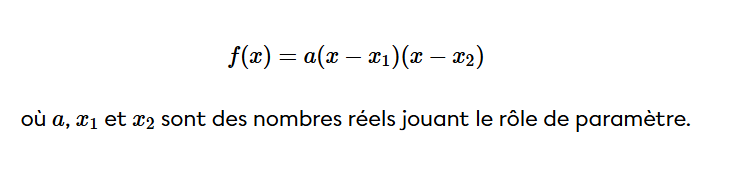Best Of
Re: Question
Salut !
Pour trouver la valeur de la constante de vitesse de réaction, il te faut utiliser la loi de vitesse.
$$ a\ \text{A} + b\ \text{B} \rightarrow c\ \text{C} + d\ \text{D} $$
$$ v = k[\text{A}]^m[\text{B}]^n $$
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne soirée !
Re: Question
Salut !
Il s'agit d'un exercice sur les calculs stœchiométriques. Ici, la première étape est de balancer l'équation de la réaction.
Puis, tu peux calculer le nombre de fer à l'aide des coefficients stœchiométriques et du nombre de mole d'aluminium.
$$ \begin{align}\color{#3A9A38}{a}\text{A}\ +\ \color{#3A9A38}{b}{\text{B}}&\rightarrow \color{#3A9A38}{c}\text{C}\ +\ \color{#3A9A38}{d}\text{D}\\\\ \dfrac{\color{#3A9A38}{a}}{\color{#3A9A38}{c}}&=\dfrac {\color{#FA7921}{n_{\text{A}}}}{\color{#FA7921}{n_{C}}}\end{align} $$
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne soirée !
Re: Question
C'est plus simple qu'il ne semble. Il suffit de procéder par étape.
Au #5, la fonction f o g (x) est:
f o g (x) = f(g(x)) = a/((ax+h) - h) + k = a/(ax) + k = 1/x + k
maintenant que vaut-elle quand l'abscisse, c'est-à-dire le x = -1/k (l'opposé de l'inverse du paramètre k), pour savoir il suffit de remplacer x par -1/k
f o g (-1/k) = 1/(-1/k) + k = -k + k = 0
Au #6, le zéro de la fonction est le x pour lequel f(x) = 0 c'est-à-dire
a(c)^(b(x-h)) + k = 0
a(c)^(b(x-h)) = -k
(c)^(b(x-h)) = -k/a
en prenant le log en base c (d'où la condition que -k/a >0), on obtient
b(x-h) = log_c (-k/a)
x - h = (1/b)log_c (-k/a)
x = h + (1/b)log_c (-k/a)
note que h = log_c (c^h)
et que (1/b)log_c (-k/a) = log_c ((-k/a)^(1/b))
consulte
https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/les-lois-des-logarithmes-m1500
pour conclure que tu as bien le résultat cherché.
Je te laisse travailler le #7
Re: Question
Salut!
Cela dépend des informations que l'on te fournit. Par exemple, si on te donne la mesure de l'aire latérale du cylindre ainsi que le rayon de la base, on sera alors en mesure de trouver la hauteur du cylindre en isolant la variable h dans la formule suivante :
Par exemple, si le rayon est de 5 cm et l'aire latérale de 25 cm², on aura alors :
$$ 25 = 2π\times 5h$$
$$ \frac{25}{2π\times 5} = h$$
$$ h = 0,796 cm$$
Voici une fiche sur cette notion : https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/l-aire-des-cylindres-m1487#
Si tu as d'autres questions, on est là!
Re: Question
Bonjour BB8Inoubliable,
Merci d’avoir utilisé la Zone d’entraide pour répondre à ta question.
Tout d’abord, on obtient la hauteur d’un cylindre en divisant le volume par la surface de base .
J’espère que cela t’as aidé. N’hésite pas à nous poser d’autres questions.
Bonne chance,
Sonia
Re: Question
Bonjour, MonarqueSage363! :)
Merci pour ta question.
Premièrement, les treize colonies étaient un groupe de colonies britanniques sur la côte atlantique de l'Amérique du Nord, qui ont eu un grand impact sur la naissance des États-Unis.
Pour te donner un peu de contexte, les colons américains (des treize colonies) étaient en colère de recevoir des taxes par leur propre gouvernement britannique sans recevoir de représentation. Ainsi, c'est ce qui mena au Boston Tea Party.
Si tu veux plus d'informations sur celui-ci, je t'invite à lire ces réponses à une question d'un autre élève :
Je t'invite aussi à consulter cette fiche sur la révolution américaine et ses conséquences, tu comprendras un peu mieux les notions sur lesquelles tu te poses des questions et l'impact que les manifestations des colons américains a eu. On y parle également du Boston Tea Party:
J'espère avoir répondu à ta question. N'hésite pas si tu en as d'autres!
Iris :)
Re: Question
Salut!
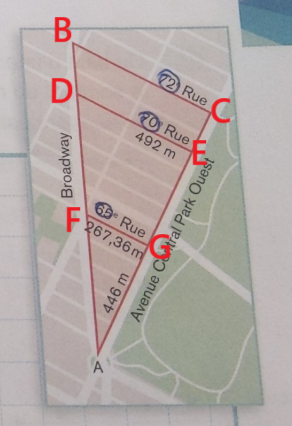
Tu peux poser ces lettres par toi-même ;)
Par exemple :
On se réfèrera alors à ton dessin pour voir ce que représente chaque lettre lorsqu'on lira tes affirmations/justifications ;)
Bonne journée! :)
Re: Question
Salut !
Ici, tu fait mention du e). L'exercice te demande simplement d'effectuer l'addition des réactions sans les changer.
C'est ce que tu fais dans la version 1. Dans la deuxième, il ne s'agit des mêmes réaction, car la stœchiométrie n'est pas respectée.
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne soirée !
Re: Question
Salut !
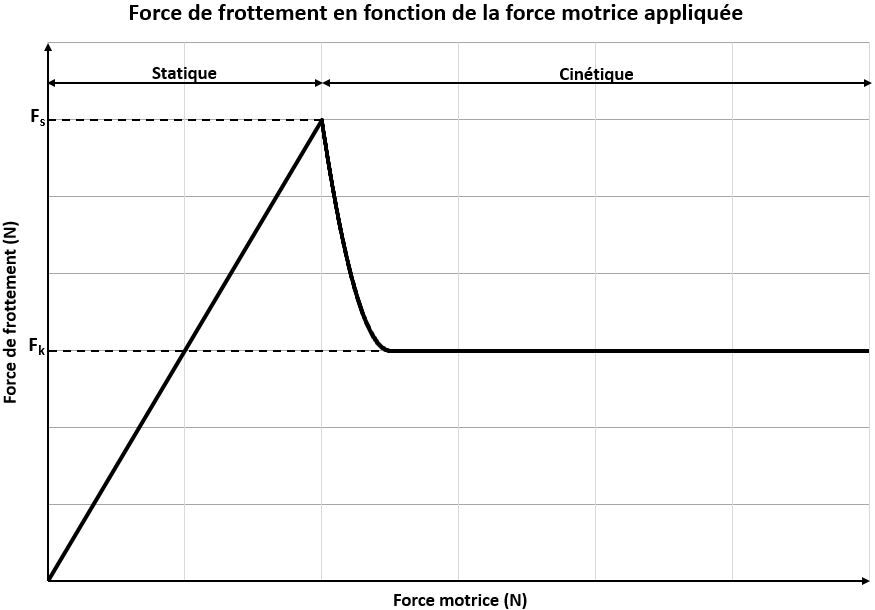
La force de frottement est une réponse à une force motrice est fluctue de cette manière :
Ainsi, pour passer d'un mode statique (sans mouvement) à du mouvement (cinétique), il te faut surpasser la force de frottement maximale. On te demande justement la force qu'il faut pour passer ce cap, juste avant la cinétique à laquelle tu fais référence.
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne soirée !
Re: Question
Salut!
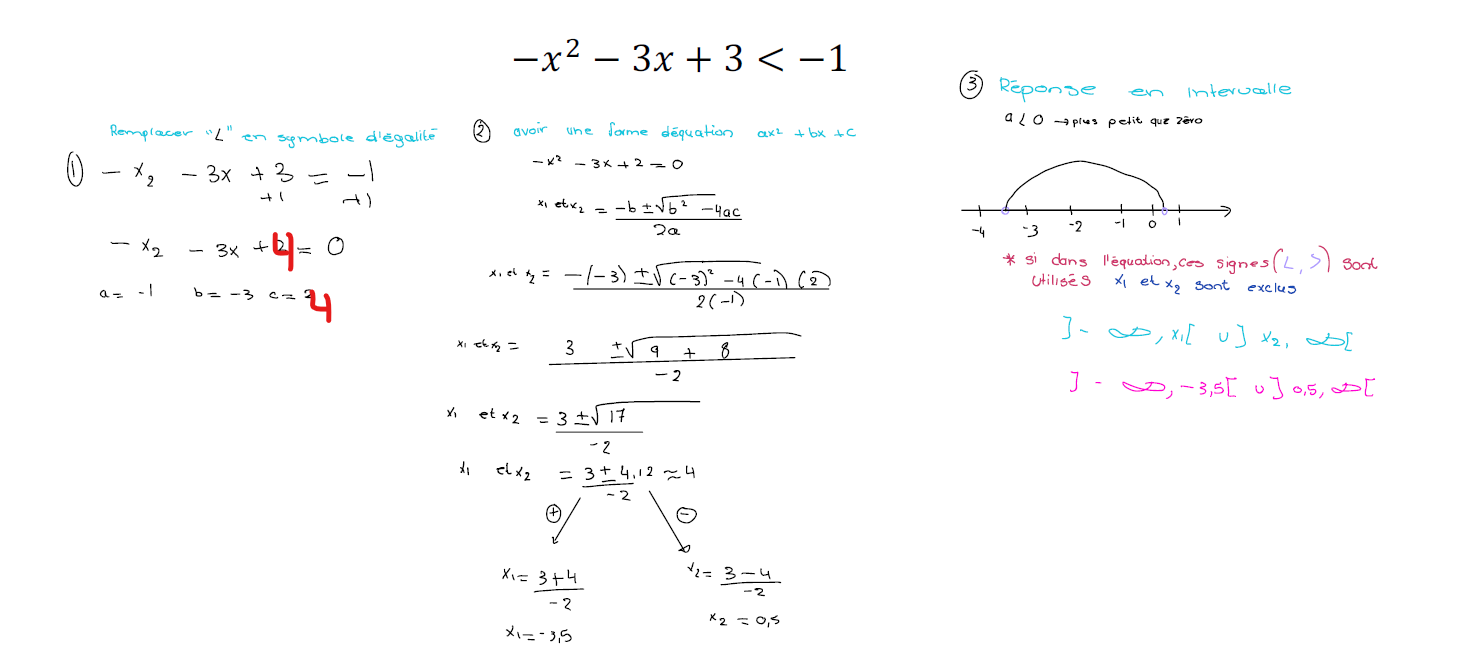
Pour le premier numéro, ta démarche est excellente, tu as juste une petite erreur de calcul ici :
Tu as additionné 1 de chaque côté pour éliminer -1 à droite, donc tu devrais obtenir c=3+1=4.
En corrigeant cette petite erreur, tu devrais obtenir la bonne réponse.
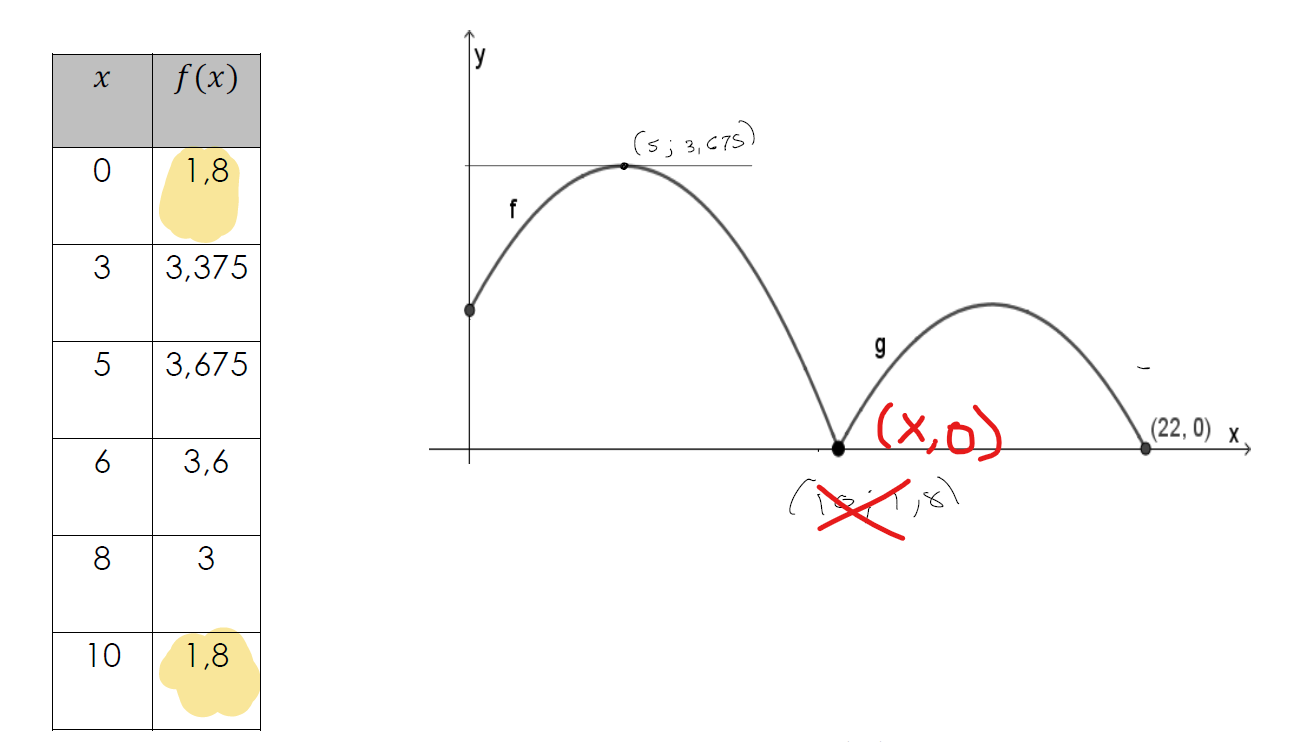
Concernant le second numéro, tu as bien commencé l'exercice. Tu as trouvé la bonne règle pour la fonction f(x). Cependant, tu dis que les coordonnées du zéro suivant sont de (10, 1.8), ce qui est faux.
Le point est sur l'axe des x, alors nécessairement, sa coordonnée en y est nulle, elle ne peut pas être égale à 1,8.
De plus, ce n'est pas parce qu'il s'agit du dernier point donné dans la table de valeurs que cela signifie nécessairement qu'il s'agisse d'un zéro de la fonction!
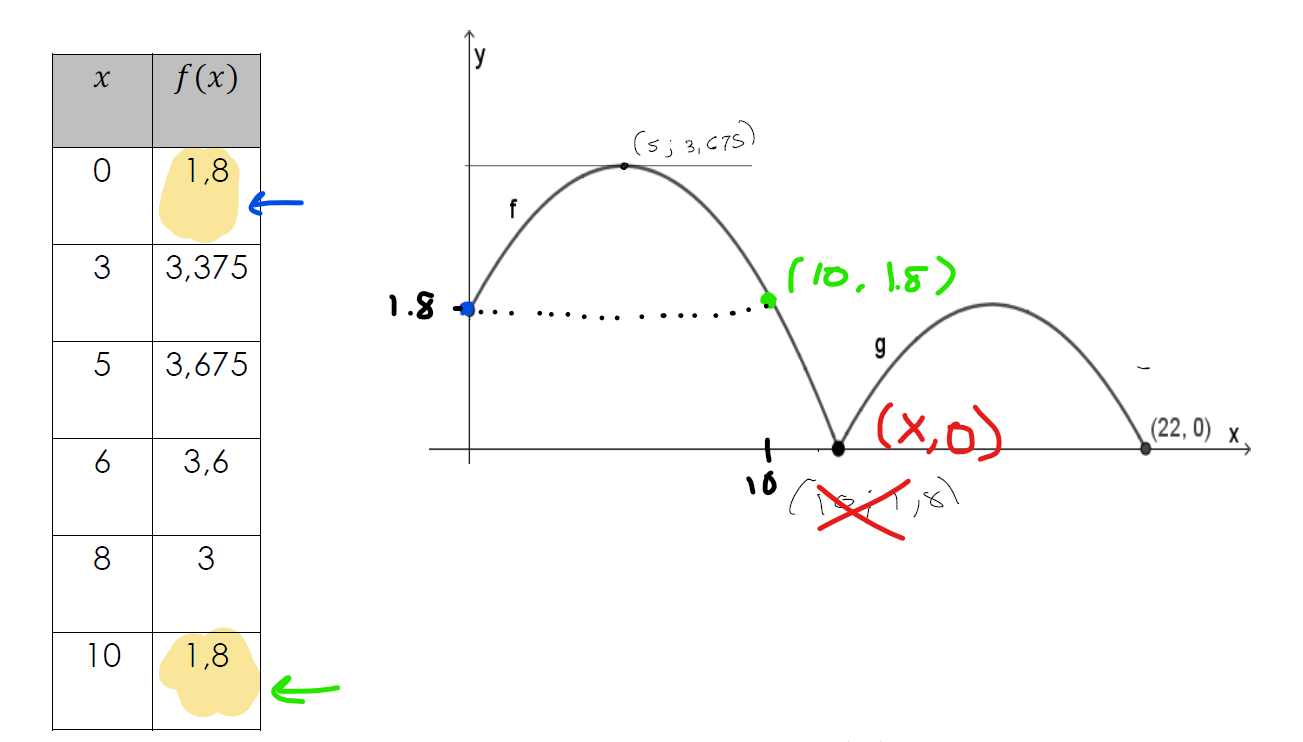
Comme tu l'avais remarqué, le premier point et le dernier point de la table de valeurs ont la même coordonnée en y (c'est ce qui nous permet justement de déduire le paramètre h de la fonction f). Donc, le point (10, 1.8) est ici :
Tu dois donc reprendre tes calculs à partir de l'étape 3.
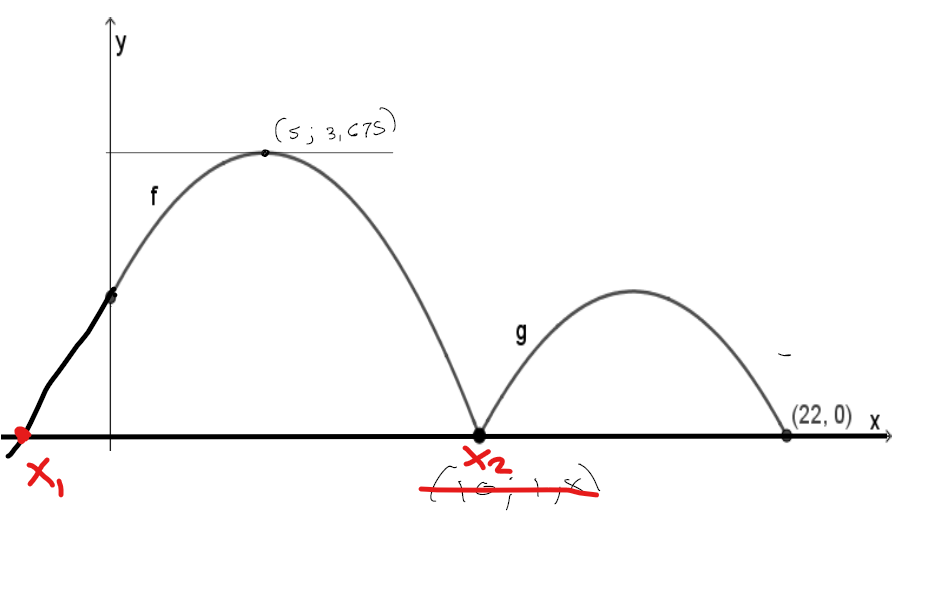
Ce que tu dois faire, c'est trouvé la coordonnée en x du second zéro de la fonction f, qui est aussi un zéro de la fonction g. Pour ce faire, tu dois résoudre l'équation suivante :
$$f(x)=0$$
$$-0,075(x-5)^2+3,675=0$$
N'oublie pas de garder le x positif seulement, puisqu'on cherche le second zéro de notre parabole g :
Une fois que c'est fait, tu peux reprendre tes calculs à ton étape 3 avec le bon x1 pour la fonction g (qui correspond au x2 trouvé de la fonction f).
De plus, le paramètre k des deux fonctions n'est pas le même (en d'autres mots, leur sommet n'ont pas la même coordonnée en y, on voit sur le graphique que le sommet de la parabole g est plus bas sur l'axe des y que celui de la parabole f). Au lieu d'essayer de trouver k, tu peux écrire l'équation de la fonction g sous forme factorisée!
Tu n'as qu'à remplacer x1 et x2 par les deux zéros de la fonction g, et tu connais déjà le paramètre a!
Voici une fiche qui pourrait t'être utile : Les formes d'écriture de la fonction polynomiale de degré 2 | Secondaire | Alloprof
J'espère que c'est plus clair pour toi! Si tu as d'autres questions, n'hésite pas à nous réécrire! :)