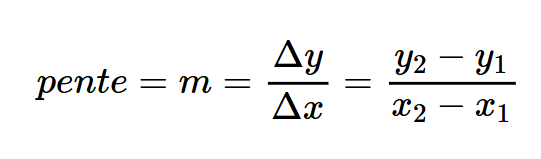Best Of
Re: Question
Salut!
Tout d'abord, la règle d'une suite a la forme suivante :
Cette règle permet de trouver un terme dans une suite de nombres ayant une certaine régularité.
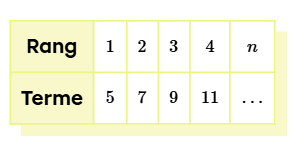
Par exemple, si on a cette suite de nombres :
Et que l'on veut trouver quel est le nombre au rang 100 (à la position 100), alors nous devons d'abord trouver la règle de la suite, puis nous allons remplacer \(n\) dans cette règle par 100, et effectuer le calcul, ce qui nous permettra de trouver le terme \(t\) qui est à n=100, c'est-à-dire au rang 100.
Voici un exemple :
On peut également faire l'inverse, soit trouver le rang d'un certain nombre. Par exemple, si on veut savoir à quelle position est le nombre 56, nous allons remplacer \(t\) par 56 dans la règle, puis résoudre l'équation pour trouver \(n\), le rang de ce terme.
Voici un exemple :
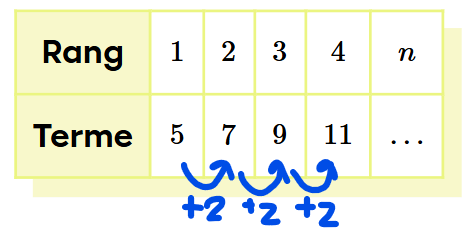
Maintenant, pour trouver la règle, il faut trouver la régularité et le terme au rang 0. Pour la régularité, aussi appelée taux de variation, ou encore la pente, il faut calculer l'écart entre deux termes consécutifs, c'est-à-dire deux termes l'un à la suite de l'autre. Si on reprend la même table de valeurs, on constate qu'on fait des bonds de 2 entre chaque terme consécutifs :
Le taux de variation est donc de 2. La règle est donc t=2n+b. Il nous reste à trouver b, le terme au rang 0. Pour cela, on sait que le terme au rang 1 est 5. Puisqu'on fait des bonds de 2, alors le terme au rang 0 est 5-2=3.
La règle est donc : t=2n+3.
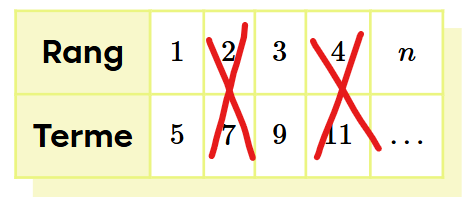
Si tu n'as pas deux termes consécutifs dans ta table de valeurs, comme ici par exemple (on fait comme si nous ne connaissions pas les colonnes barrées) :
Alors on doit utiliser cette règle :
où les y sont les termes et les x sont les rangs.
En appliquant cette formule, on peut obtenir notre taux de variation de 2 :
$$régularité=\frac{9-5}{3-1}=\frac{4}{2}=2$$
En fait, cette formule est toujours applicable pour trouver le taux de variation, même lorsque les nombres sont consécutifs.
$$régularité=\frac{7-5}{2-1}=\frac{2}{1}=2$$
Donc, tu peux toujours utiliser cette formule pour trouver la régularité d'une suite, et ce, en utilisant 2 couples de cette suite, peu importe lesquels.
Voici une fiche sur cette notion qui pourrait t'être utile : La règle d'une suite | Secondaire | Alloprof
J'espère que c'est plus clair pour toi! N'hésite pas à nous réécrire si tu as d'autres questions! :)
Re: Question
Salut!
Merci à toi de choisir nos services! Nous apprécions énormément tes mots chaleureux, et cela signifie beaucoup pour nous de savoir que notre aide compte vraiment pour toi! Je transmettrai ton beau message au reste de l'équipe et à Laurie. :)
N'hésite jamais à revenir si tu as d'autres questions! :)
Re: Question
Bonjour CielRose9102
Merci d’utiliser la zone d’entraide de Alloprof !
De ce que je peux comprendre, tu as peut-être fais une petite erreur dans la formulation de ta question. Il s'agit de l'algèbre et non de lageb.
Au secondaire, on apprend l'algèbre qui est une forme de mathématiques plus complexe. En effet, c'est à ce stage qu'on inclut des lettres de l'alphabet dans les mathématiques, on les utilises comme inconnues afin de résoudre des équations plus complexes.
Ne t'inquiètes pas, cette matière est bien expliquée par les professeurs et tu vas trouver ça aussi facile que ce que tu fais maintenant!
Voici un lien qui peut te donner une idée : https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/algebre-expressions-algebriques-m1068
Ne lâche pas !
DragonSigma9922
Re: Question
Salut!
L'algèbre est une branche des mathématiques qui utilise des lettres et des symboles pour représenter des nombres et exprimer des relations entre eux. Elle permet de résoudre des équations et de manipuler des expressions mathématiques de manière générale. Voici un exemple :
Imaginons que nous avons une boîte de bonbons. Nous ne savons pas combien il y a de bonbons dans cette boîte, alors nous dirons qu'il y a "x" bonbons. Si chaque bonbon coûte 2$, et qu'au total, nous payons 10$, alors nous avons l'équation :
$$ 2 \times x=10 $$
Cela signifie que le coût total des bonbons (2x) est égal à 10$. Maintenant, pour trouver combien de bonbons il y a dans la boîte, nous devons trouver la valeur de la lettre x. Pour ce faire, il faut résoudre cette équation algébrique. On trouvera alors que x=5, ce qui signifie qu'il y a 5 bonbons dans la boîte.
Cette notion n'est étudiée qu'à partir du secondaire. Si tu es tout de même curieux/curieuse d'en apprendre davantage à ce sujet, tu peux consulter la section "algèbre" de cette fiche : Aide-mémoire – Mathématiques – Secondaire 1 et 2 | Secondaire | Alloprof
Bonne journée! :)
Re: Question
Salut AntimoineAlerte1056 😁
Merci pour ta question!
Selon le Bescherelle, c'est au choix dans ce cas, tu peux écrire un ou l'autre.
Cependant, selon la graphie rectifiée, en vigueur depuis 1998 au Québec, on recommande l'utilisation de demandè-je, comme on le prononce. Tu retrouveras cette proposition, par exemple, dans Antidote.
Écris-nous si tu as d'autres questions. 😊
À bientôt sur la Zone d'entraide! 😎
Re: Question
Salut RubisAdorable979!
Merci d'utiliser la zone d'entraide pour poser tes questions. J'espère que tu vas bien.
La phrase syntaxique est une unité de sens qui contient au moins les deux constituants obligatoires (sujet et prédicat) et parfois aussi le complément de phrase qui, lui, reste facultatif.
Observe les exemples suivants :
Éric marche en forêt.
Éric marche en forêt tous les dimanches.
Tu peux considérer comme phrase graphique toute phrase qui commence par une majuscule et qui se termine par un point (d'interrogation, d'exclamation ou de suspension).
Observe l'exemple suivant :
Avant le diner, Éric tondra la pelouse et Isabelle taillera les arbres.
Grâce à cet exemple, tu comprends donc qu'une phrase graphique peut contenir plusieurs phrases syntaxiques.
Si jamais tu voulais en apprendre davantage sur les différences entre les phrases graphiques et les phrases syntaxiques, je te conseille de consulter la fiche notionnelle ci-dessous.
J'espère avoir répondu à tes questions. N'hésite pas à revenir nous voir si jamais tu en avais d'autres.
Je te souhaite une belle soirée!
Sébastien.
Re: Question
Bonjour,
Faisons le calcul ensemble :
0 = 2 tan(-3b) + 2
-2 = 2 tan(-3b)
-1 = tan(-3b)
acrtan(-1) = -3b
-pi/4 = -3b
(-pi/4)/-3 = b
b = (pi/4)/3 = (pi/4) * 1/3 = pi/(4*3) = pi/12
S'il y a une étape de la démarche que tu ne comprends pas, dis le nous et cela nous fera plaisir de te l’expliquer !
Bonne journée
Re: Question
Bonsoir CyborgCalme1704!
Je ne comprends très bien ta question. Est-ce que tu veux dire:
"Comment diminuer la vitesse de rotation d'un organe mené?"
Si c'est le cas, il est question des systèmes de transmission du mouvement.
Il est possible de provoquer un changement de vitesse lorsque le diamètre de l'organe menant et celui de l'organe mené sont différents.
Il existe différents types de système de transmission de mouvement mais le principe de base pour qu'un organe mené tourne moins vite qu'un organe menant est que:
" son diamètre soit plus grand que celui de l'organe menant ou moteur."
Autrement dit, plus une roue est grande moins elle fera de tours de rotation que celle qui l'entraîne.
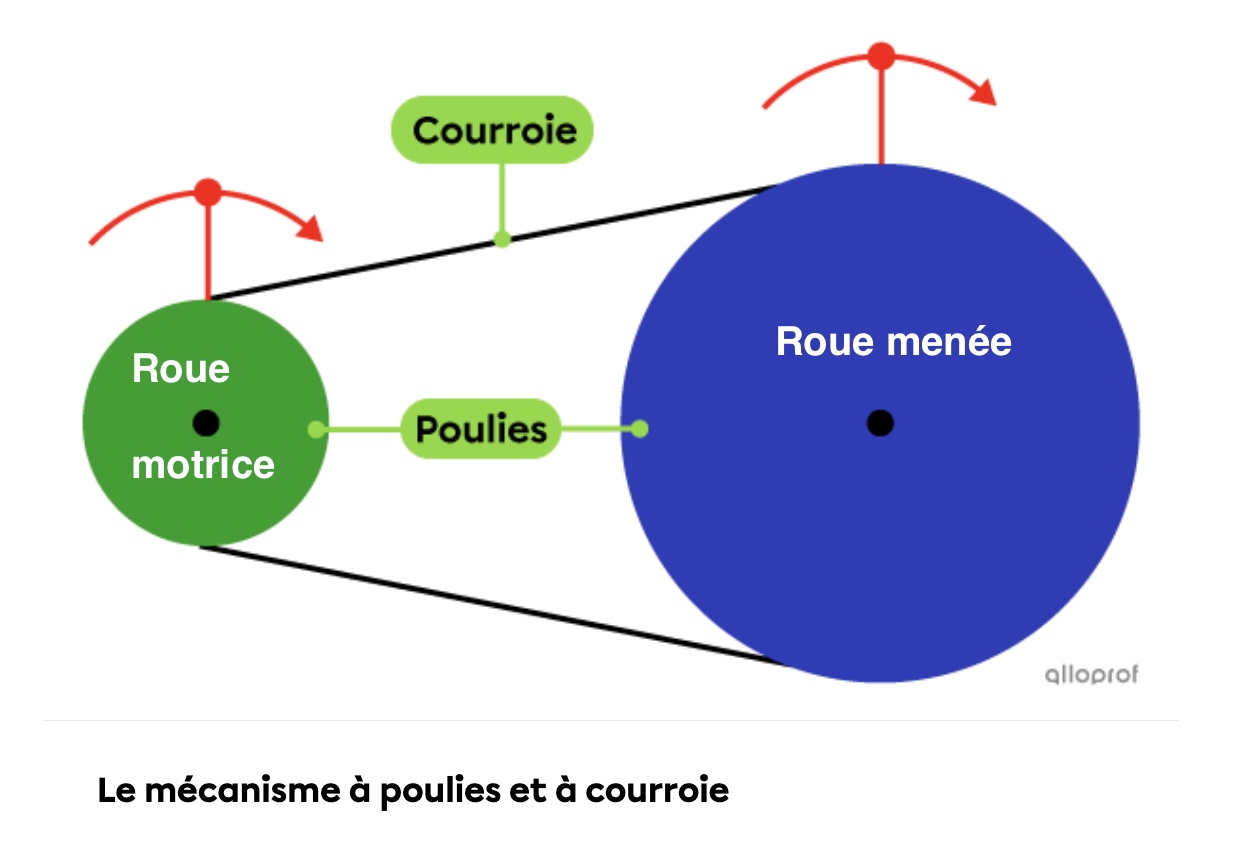
Exemple:
Donc ici la roue motrice va tourner plus vite que la roue menée parce que son diamètre est plus petit que celui de la roue menée.
J'ai utilisé l'illustration que l'on retrouve dans notre fiche sur les systèmes de transmissions de mouvement que tu peux consulter via ce lien:
Il y a aussi cette très belle fiche avec des animations qui pourraient t'aider:
J'espère avoir répondu à ta question.
N’hésite pas à nous écrire à nouveau si tu as d’autres questions.
Bien à toi,
ThonLucide8631
Re: Question
Merci d’avoir utilisé la zone d’entraide Alloprof QuartzComique3516! Pour convertir des kilogrammes en grammes, il suffit de multiplier le nombre de kilogrammes par 1000, car 1 kg équivaut à 1000 g. Par exemple, si on veut convertir 2 kg en grammes, on fait 2 × 1000 = 2000 g. De même, 0,5 kg correspond à 500 g. À l’inverse, pour passer des grammes aux kilogrammes, on divise par 1000. Par exemple, 3000 g = 3000 ÷ 1000 = 3 kg.
TortueFantastique6849