Populaires
Re : Question
Re-salut !
Parfait ! Résolvons-le ensemble :
$$ (\frac{1}{2})^{\frac{20}{t_{1/2}}} = 0.25$$
Pour ce faire, tu dois te servir des lois des logarithmes. On utilise les logarithmes parce que l’inconnue (t_1/2) se trouve dans un exposant.
Les logarithmes sont justement l’outil qui permet de faire descendre un exposant pour pouvoir le manipuler.
Rappel : log(a^b) = b · log(a)
Ainsi,
$$ (\frac{1}{2})^{\frac{20}{t_{1/2}}} = 0.25$$
$$ \log{(\frac{1}{2})^{\frac{20}{t_{1/2}}}} = \log{0.25} $$
$$ \frac{20}{t_{1/2}}} * \log{(\frac{1}{2}) = \log{0.25} $$
Je te laisse poursuivre la résolution.
Voici un lien utile :
N'hésite pas à revenir nous voir si tu bloques toujours !
Bonne journée :)
Re : Question
Bonsoir ElfeFantastique7510 😊
Ne t'en fais pas, les cosinus sont dure à comprendre au début!
L’idée clé ici est de transformer l’équation trigonométrique en une équation algébrique simple.
On part de 2(cosx)^2-cosx = 3 et on regroupe tout du même côté. On obtient donc 2(cosx)^2-cosx-3=0
Ici on peut donc faire une substitution. On pose u=cosx. L'équation devient alors 2u^2-u-3=0. Cette équation est de la forme d'une fonction polynomiale de degré deux, on peut donc la traité de la même façon qu'on le ferait dans le cas d'une fonction polynomiale.
En factorisant on obtient: (2u-3)(u+1)=0. Ainsi, u=3/2 ou u=-1.
On revient maintenant à cosx. Comme le cosinus d’un angle est toujours compris entre −1 et 1, la valeur 3/2 est impossible. Il reste donc seulement cosx=−1.
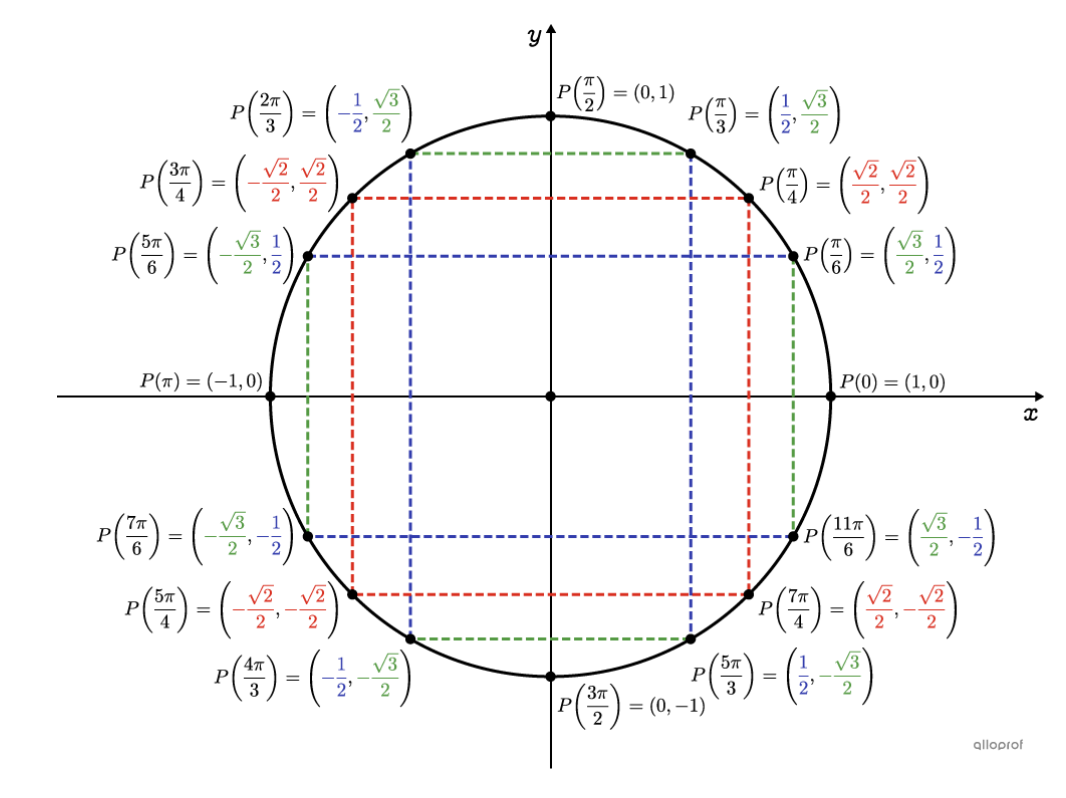
Sur le cercle trigonométrique, le cosinus vaut −1 lorsque l’angle correspond à un point complètement à gauche du cercle, c’est-à-dire pour les angles de la forme x=π+2k, où k est un entier.
Il ne reste qu’à vérifier quels angles de cette forme se trouvent dans l’intervalle [−3π,0][−3π,0].
Si on prend k=−2k, on obtient x=−3π.
Si on prend k=−1, on obtient x=−π.
Ces deux valeurs sont bien dans l’intervalle demandé.
Donc, la solution finale est bien x∈{−3π, −π}
En espérant que ceci te débloquera. Si jamais tu as d'autres questions, n'hésite surtout pas!
Mélodie 🎶
Re : Question
Salut PerleInoubliable3024 😊
Ne t'en fais pas, c'est un sujet assez difficile a comprendre au début.
Premièrement, l'homothétie est une transformation géométrique qui permet d'agrandir ou de réduire une figure selon un rapport d'homothétie k et un centre O. Ainsi, une homothétie a pour conséquence d'augmenter ou de diminuer de façon proportionnelle les mesures des côtés d'une figure.
Imagine que tu prends une photo avec ton cellulaire. Quand tu zoomes sur la photo, elle devient automatiquement plus grande. Par contre, la forme de ton image reste la même. C'est la même chose quand tu dézoomes, l'image devient alors plus petite sans toutefois se déformer. Les mesures des côtés de la figure reste les mêmes à un rapport près.
On nomme ce rapport le rapport de similitude ou bien d'homothétie (k).
Le rapport de similitude (k) est un rapport entre des longueurs homologues (côtés, périmètres, rayons, circonférences, etc.) de 2 figures semblables. Pour le calculer, on utilise cette formule:
Le rapport de similitude indique l'impact qu'aura la transformation sur la forme obtenu. Pour t'aider, voici un tableau indiquant ce que représente la valeur de k:
Plusieurs résolutions sont possibles en lien avec l'homothétie. On peut te demander de construire une figure par homothétie, de trouver le centre d'homothétie, de calculer le rapport d'homothétie ou bien de tracer une homothétie dans le plan.
J'ai trouvé cette fiche pour toi, tu y retrouveras les différents types de résolution en lien avec l'homothétie:
Si jamais tu avais des questions en lien avec un numéro en particulier, n'hésite surtout pas. Ne te décourage pas, c'est avec la pratique que l'on devient meilleur :)
Bonne soirée
Mélodie 🎶
Re : Question
Merci pour ta question!
Il y a plusieurs manières de résoudre des problèmes sur les circuits électriques mixtes. Cependant, la meilleure manière est possiblement de réduire les circuits le plus possibles.
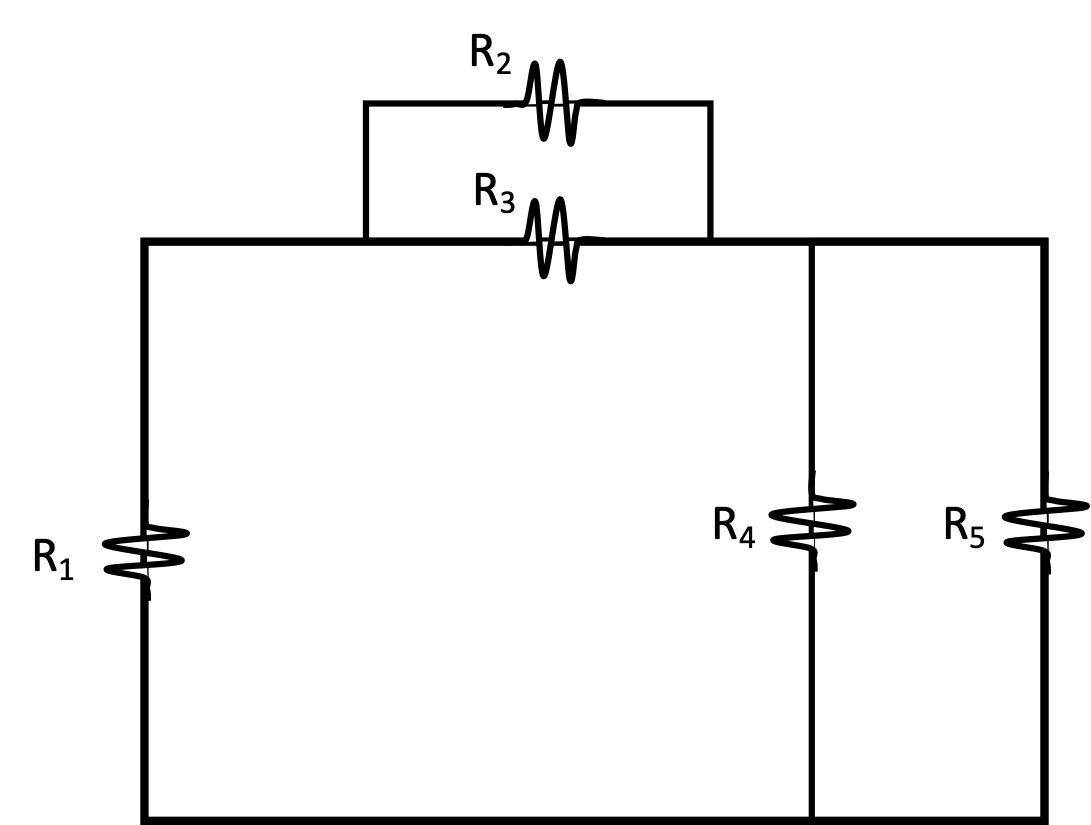
Spécifiquement, grâce aux calculs dans les circuits électriques, tu peux simplifier des circuits électriques. Par exemple, imaginons le circuit électrique suivant :
Il y a 5 résistances dans ce circuit, dont 4 en parallèle. En fait, grâce aux résistances équivalentes, on peut combiner les résistances 2 et 3, et 4 et 5, respectivement, en utilisant la relation suivante :
$$ \frac{1}{R_{éq}} = \frac{1}{R_1} + \frac{1}{R_2} $$
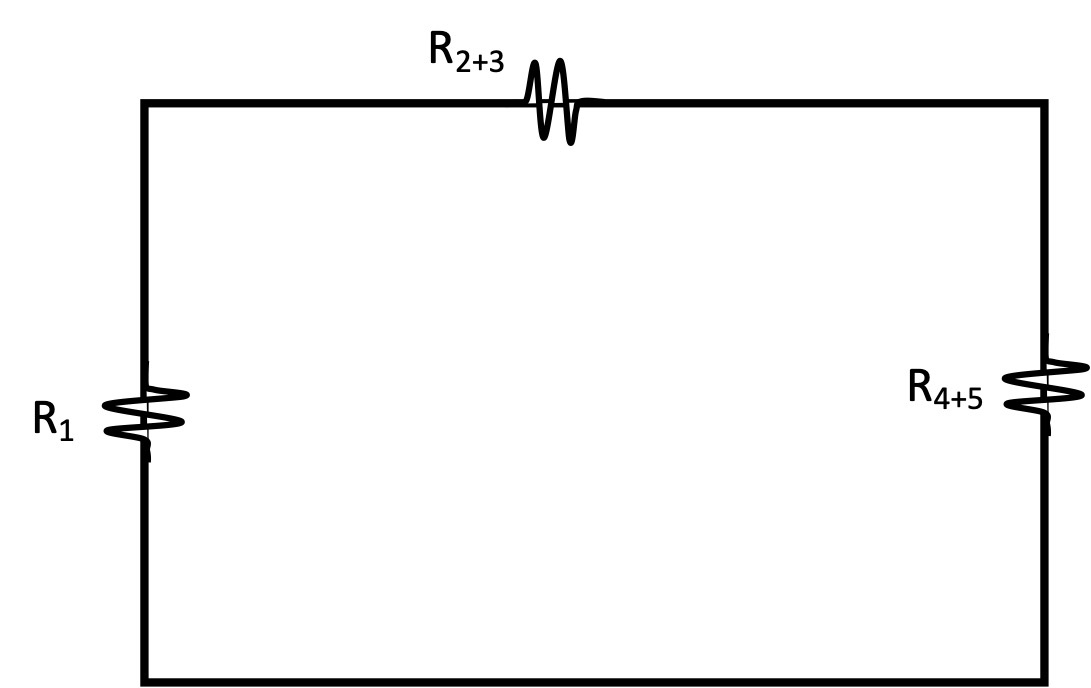
Puis, tu pourrais tout réunir les résistances sous une seule grâce à la relation suivante, car toutes ces résistances sont en série :
$$ R_{éq} = R_1 + R_{2+3} + R_{4+5} $$
Cette fiche du site d'Alloprof explique les calculs dans les circuits électriques :
N'hésite pas si tu as d'autres questions!
Re : Question
Bonjour LionBrave5270,
Merci d'utiliser nos services!
Je t'invite à aller consulter la réponse d'un de mes collègues à une question similaire à la tienne. Il explique en détail comment résoudre des problèmes avec des circuits mixtes.
Voici sa réponse :
J'espère t'avoir aidé. N'hésite pas si tu as d'autres questions!
Zachary T. :)
Re : Question
Bonjour,
Merci d'utiliser nos services!
La force appliquée représente la force que l'on applique sur un objet pour le mettre en mouvement. Elle varie beaucoup selon les situations.
La force efficace est la composante de la force appliquée qui est parallèle au déplacement d’un objet. La force efficace a la même orientation que le déplacement.
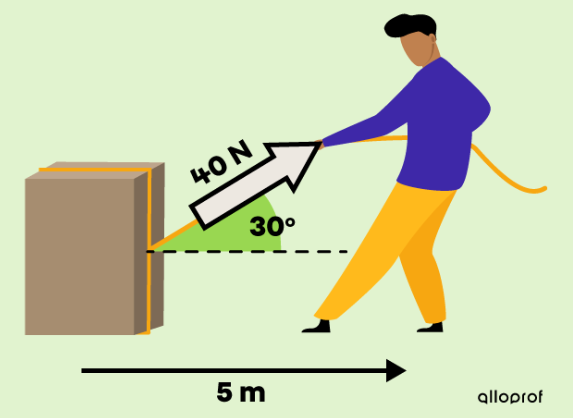
Par exemple, si on tire une corde comme dans l'image ci-dessous :
Dans ce cas-ci, la force appliquée représente la force que l'on utilise pour tirer la boite, soit la force de 40 N à 30° (la flèche blanche).
La force efficace, elle, correspond à la composante de la force appliquée qui est dans la même direction que le mouvement. Dans l'image, il s'agirait des pointillés. On pourrait tracer une flèche de la boite au garçon. On peut déterminer sa valeur grâce à la trigonométrie.
Voici une fiche qui pourrait t'être utile :
J'espère t'avoir aidé. N'hésite pas si tu as d'autres questions!
Zachary T. :)
Re : Question
Les colloïdes sont bien des mélanges homogènes. En effet, il ya deux types de mélange homogène: les solutions et les colloïdes. Les solutions sont des mélanges de deux substances ou plus dont les constituants ne peuvent pas être distingués à l’œil nu et non plus grâce à un instrument microscopique. Cependant, les colloïdes sont de la même définition sauf le fait qu’on peut bien distinguer les constituants d’un colloïdes grâce a un instrument d’observation précis (pas à l’œil nu).
Re : Question
Bonjour PoutineFormidable321 😊,
Merci d'utiliser la zone d'entraide pour poser tes questions! En effet, la notion de colloïde peut sembler ambiguë. Pour bien la comprendre, nous nous pencherons un peu plus sur ce qu'est un mélange.
Un mélange est une association de plusieurs substances qui ne produisent pas de réactions chimiques entre elles. Il en existe trois types:
1- Les mélanges homogènes
2- Les mélanges hétérogènes
3- Les colloïdes!
Un mélange est hétérogène si on peut si on peut y distinguer plusieurs constituants à l'oeil nu. Par exemple, une soupe est un mélange hétérogène puisqu'on peut distinguer différents légumes et le bouillon à l'oeil nu.
Un mélange est homogène si on peut distinguer qu'un seul constituant à l'oeil nu. Par exemple, l'air est un mélange homogène. En effet, il est composé de plusieurs gaz (dioxygène, diazote et autres gaz), mais on ne peut pas les distinguer.
Un colloïde, c'est un mélange hétérogène, mais qui a l'air homogène. À l'oeil nu, le mélange semble homogène, mais si on utilise des instruments pour voir microscopiquement, nous pourrions distinguer plusieurs constituants différents. Le sang, par exemple est un colloïde puisqu'il semble homogène à l'oeil nu, mais on pourrait distinguer le plasma, les globules rouges, les globules blancs, etc., au microscope.
Pour aller plus loin, tu peux toujours consulter la fiche sur les mélanges :
N'hésite pas si tu as d'autres questions!
Re : Question
Bon matin PistacheMagnifique7230 😊
Merci pour cette belle question✨
Les réciproques sont parfois dures à comprendre au départ, mais tu as un très bon réflexe de venir chercher de l'aide :)
☀️La réciproque d'une fonction f s'obtient en intervertissant les valeurs de x et de y puis en isolant y. Elle se note f^−1. On obtient le graphique d'une réciproque en faisant subir à notre fonction une réflexion par rapport à l'axe y=x.
⚡️Nous avons justement une fiche alloprof te donnant des exemples de démarche à suivre pour trouver la réciproque d'une fonction affine:
Également, voici des exercices pour te pratiquer sur ce sujet:
Si jamais tu avais d'autres questions, n'hésite surtout pas!
Je te souhaite que ta révision et ton examen ce passe bien. N'abandonne surtout pas :)
Mélodie 🎶
Re : Question
Bonjour HothBrave4650 😊
C'est une très bonne question!
Pour multiplier des fractions, il faut multiplier les numérateurs ensemble et les dénominateurs ensemble. On obtient ainsi une nouvelle fraction qui correspond au produit final.
Par exemple, si tu veux multiplier 2/5 par 3/4, tu devras commencer par multiplier les deux numérateur (2 et 3) ensemble, tu obtiens donc 6 qui sera ton nouveau numérateur. Ensuite, tu fais la même chose pour les dénominateurs. Tu obtiens donc 5x4=20. Ainsi, ton nombre final sera 6/20.
Voici une petite vidéo pour t'aider:
Également, nous avons une fiche parfaite pour toi!
Si jamais tu as d'autres questions, n'hésite surtout pas!
Mélodie 🎶