Subjects
Grades
When looking for the rule of an absolute value function, there are 3 possible cases. In each case, use the simplified functional form: |f(x)=a\vert x-h\vert+k.|
To find the rule of an absolute value function when we know the coordinates of the vertex and any other point of the function, use the equation in functional form.
Replace parameters |h| and |k| with the coordinates of the vertex.
Calculate |a| by replacing |x| and |y| with the coordinates of the other point.
Write the rule.
Determine the rule of the absolute value function with a vertex of |(-3, -2)| and another point where the coordinates are |(-4, -5).|
Replace parameters |\boldsymbol{h}| and |\boldsymbol{k}| with the coordinates of the vertex
||\begin{align}f(x)&=a\vert x-\color{#3b87cd}h \vert +\color{#3a9a38}k\\f(x) &=a\vert x-\color{#3b87cd}{-3} \vert +\color{#3a9a38}{-2} \\ f(x) &= a\vert x+3\vert -2 \end{align}||
Calculate |\boldsymbol{a}| by replacing |\boldsymbol{x}| and |\boldsymbol{y}| with the coordinates of the other point
||\begin{align} \color{#ff55c3}{-5} &= a\vert \color{#ff55c3}{-4}+3\vert -2 \\ -5 &= a\vert -1\vert -2 \\ -5 &= a(1)-2\\ -5 &= a-2\\ -3&=a \end{align}||
Write the rule
The rule of the function is |f(x)=-3\vert x+3\vert -2.|

Moments in the video:
To find the rule of an absolute value function when we know 2 points with the same |(y)|-value and a third point, we must find the slope of the function’s 2 branches.
Plot the points on the Cartesian plane.
Calculate the value of parameter |h| by calculating the average of the |x|-values of the 2 points with the same |y|-value.
Calculate the slope of the line passing through the 2 points located on the same side of the vertex (on the same branch).
Determine the sign of parameter |a| by analyzing if the function opens upwards or downwards.
Replace the values of parameters |h| and |a| calculated in Step 4.
Calculate |k| by replacing |x| and |y| with the coordinates of a point.
Write the rule.
In an absolute value function, the 2 branches are symmetrical. So, parameter |a|, the slope of the left branch |(a_1),| and the slope of the right branch |(a_2)| all have the same value if we ignore the signs.
The Opening is Upwards
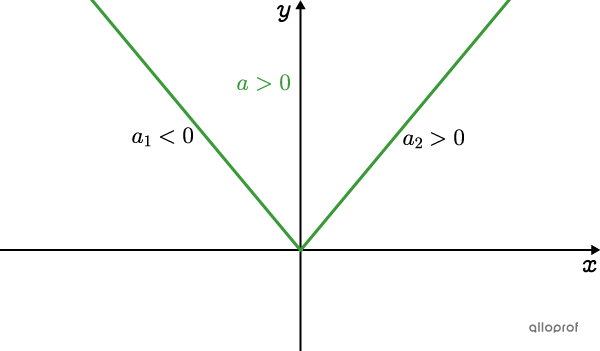
The slope of the left branch is negative as it is decreasing |(a_1<0).|
The slope of the right branch is positive as it is increasing |(a_2>0).|
Parameter |a| of the absolute value function is positive |(\color{#3A9A38}{a>0}).|
The Opening is Downwards
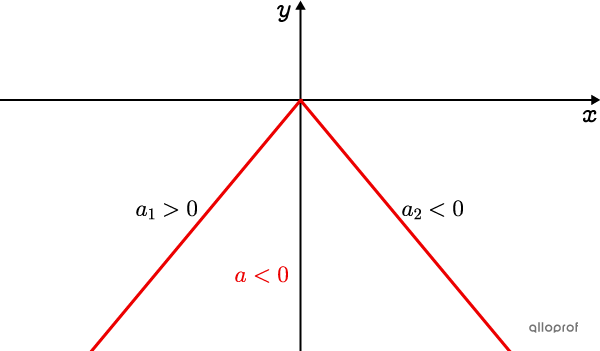
The slope of the left branch is positive as it is increasing |(a_1>0).|
The slope on the right branch is negative as it is decreasing |(a_2<0).|
Parameter |a| of the absolute value function is negative |(\color{#EC0000}{a<0}),| because the curve has been reflected across the |x|-axis.
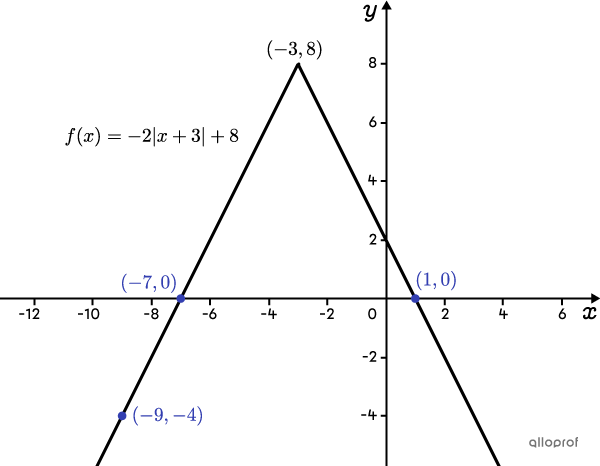
Determine the rule for the absolute value function where the zeros are |-7| and |1,| and passes through the point |(-9,-4).|
Plot the points on the Cartesian plane
Analyzing their position, points |(-9,-4)| and |(-7,0)| are located on the same branch of the absolute value function and point |(1,0)| is on the other branch. Therefore, the vertex of the function is above the |x|-axis and the graph opens downwards.
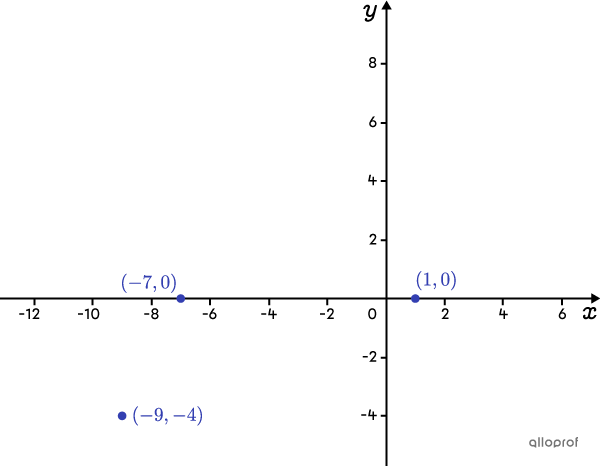
Calculate the value of parameter |\boldsymbol{h}| by calculating the average of the |\boldsymbol{x}|-values of the 2 points with the same |\boldsymbol{y}|-value.
In this case, the two points with the same y-value are the zeros located at |x=-7| and |x=1.| The |x| value of the vertex corresponding to parameter |h| is exactly in the middle of the two zeros, because the graph of an absolute value function is symmetrical. ||\begin{align}h&=\dfrac{-7+1}{2}\\h&=-3\end{align}||
Calculate the slope of the line passing through the 2 points located on the same side of the vertex (on the same branch)
The points |(-9,-4)| and |(-7,0)| are located on the same branch to the left of the vertex. Calculating the slope of the line |(a_1)| passing through the points:
||\begin{align}a_1&=\dfrac{y_2-y_1}{x_2-x_1} \\ &=\dfrac{0--4}{-7--9} \\ &=2\end{align}||
Determine the sign of parameter |\boldsymbol{a}| by analyzing if the function opens upwards or downwards
Since the graph opens downwards, parameter |a| must be negative.
|a=-2|
Replace the values of parameters |\boldsymbol{h}| and |\boldsymbol{a}| calculated in Step 4||\begin{align}f(x)&=\color{#ec0000}a\vert x-\color{#3b87cd}h \vert +k\\f(x) &=\color{#ec0000}{-2}\vert x-\color{#3b87cd}{-3} \vert +k\\ f(x) &=-2\vert x+3 \vert +k\end{align}||
Calculate |\boldsymbol{k}| by replacing |\boldsymbol{x}| and |\boldsymbol{y}| by the coordinates of a point
We use the point |(1,0):|
||\begin{align} \color{#ff55c3}{0} &= -2\vert \color{#ff55c3}{1}+3\vert +k \\ 0 &= -2\vert 4\vert +k \\ 0 &= -2(4) +k \\ 0&=-8+k \\ 8 &= k \end{align}||
Write the rule
The rule for this absolute value function is |f(x)=-2\vert x+3\vert +8.|

Moments in the video:
To determine which points are on the same branch when 3 points on the graph, there are a few things to keep in mind:
Never assume any of the given 3 points is the function’s vertex, unless specified.
Always make sure that the symmetry between the 2 branches is respected.
Consider the following figure:
Are the points |A| and |B| on the same branch, or are points |B| and |C|?
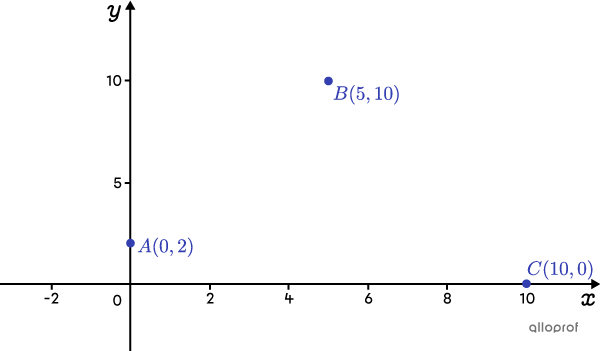
If |A| and |B| are on the same branch, the slope of the branch can be calculated: ||a_1=\dfrac{10-2}{5-0}=\dfrac{8}{5}||
Since the 2 branches must be symmetrical, the slope of the other branch passing through the point |C| is the same, but negative. ||a_2=-\dfrac{8}{5}||
Next, graph the line |AB| and the line passing through |C,| where the slope is |-\dfrac{8}{5}.|
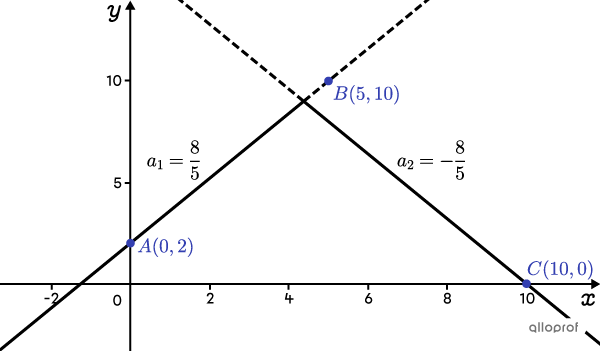
Note that the vertex is lower than the point |B.| In other words, point |B| is not located on either of the 2 branches of the absolute value function, but on an extension of a branch, which does not make sense. This means that points |A| and |B| are not on the same branch.
If |B| and |C| were instead on the same branch, the slope of the branch can be calculated: |a_2=\dfrac{10-0}{5-10}=-2.| Therefore, the slope of the left branch is equal to |2| and we obtain the following graph which confirms it is the right choice.

Note that in each case, point |B| is not the vertex of the function.
To find the rule of an absolute value function when we don’t know the coordinates of the vertex or have 2 points located at the same height (same y-coordinate) on the Cartesian plane, we create a system of equations and use the comparison method to solve it. An example is written below.
Plot the points on the Cartesian plane.
Calculate the slope of the line passing through the 2 points on the same side of the vertex (on the same branch).
Find the rule in the form |y=ax+b| of the 2 branches.
Find the coordinates of the vertex (i.e., the intersection point of the two branches) using the comparison method.
Determine the sign of parameter |a| by analyzing the opening of the function.
Write the rule by replacing the values of parameters |a,| |h,| and |k.|
Find the rule of the absolute value function passing through the points |(1,2),| |(7,-6,)| and |(-1,-2).|
Plot the points on the Cartesian plane
Analyzing their position, points |(-1,-2)| and |(1,2)| are located on the same branch, and point |(7,-6)| is on the other branch of the absolute value function graph. Therefore, the vertex of the function will be above the |x|-axis and it will open downwards.
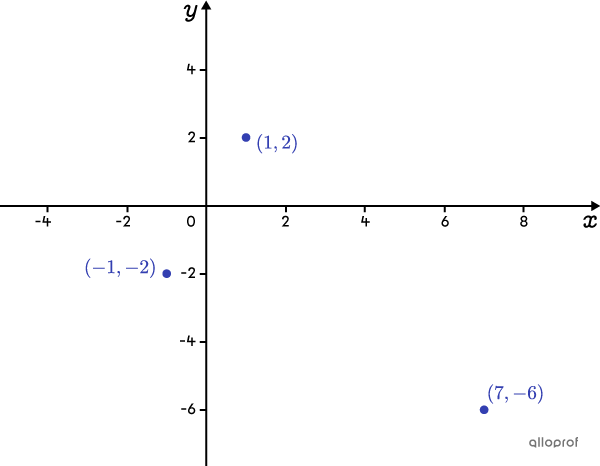
Calculate the slope of the line passing through the 2 points on the same side of the vertex (on the same branch)
The 2 points on the same branch are |(-1, -2)| and |(1,2).|
||\begin{align}a_1&=\dfrac{y_2-y_1}{x_2-x_1}\\&=\dfrac{2--2}{1--1}\\&=2\end{align}||
Find the rule in the form |\boldsymbol{y=ax+b}| of the 2 branches
For the left branch, |a| is positive as the line is increasing. Using the point |(-1,-2)| to calculate |b_1:|
||\begin{align} y_1&=a_1x+b_1 \\ -2 &= 2 (-1) + b_1\\ -2 &= -2 + b_1 \\ 0 &=b_1 \end{align}||
So, the rule for this branch is |y_1=2x.|
For the right branch, |a| is the same but negative. Using the point |(7,-6)| to calculate |b_2:|
||\begin{align} y_2&=a_2x+b_2 \\ -6 &= -2 (7) + b_2 \\ -6 &= -14 + b_2 \\ 8&=b_2 \end{align}||
So, the rule for this branch is |y_2=-2x+8.|
Find the coordinates of the vertex (i.e., the intersection point of the two branches) using the comparison method||\begin{align} y_1&=y_2 \\ 2x &= -2x + 8 \\ 4x&=8\\x&=2 \end{align}||
So, |h=2.|
To find |k,| replace |x| by |2| in either of the 2 rules. ||\begin{align} \begin{aligned}y_1 &= 2x \\ &= 2 (2) \\ &=4\end{aligned}\quad \begin{aligned}y_2 &= -2x+8 \\ &= -2 (2)+8 \\ &=4\end{aligned} \end{align}||
So, |k=4.|
Determine the sign of parameter |\boldsymbol{a}| by analyzing the opening of the function
Since the opening is downwards, parameter |a| is negative.
So, |a=-2.|
Write the rule by replacing the values of parameters |\boldsymbol{a,}| |\boldsymbol{h,}| and |\boldsymbol{k}|
Replacing the values in the functional form of the rule of an absolute value function:||\begin{align}f(x)&=a\vert x-h\vert +k\\f(x)&=-2\vert x-2\vert +4\end{align}||
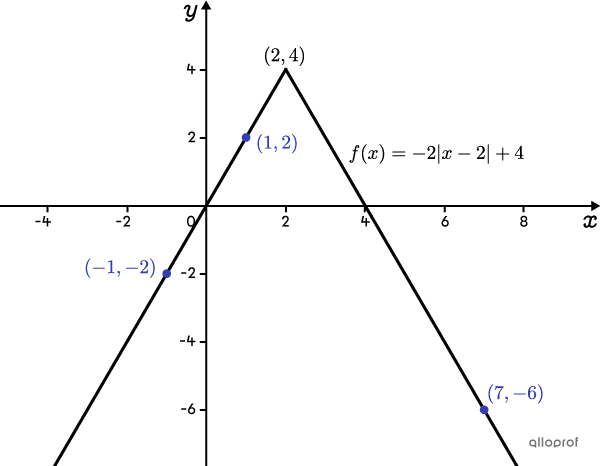

Moments in the video: