Subjects
Grades
The inverse of an absolute value function is comprised of 2 rays that stem from the same point and form a sideways V. The domain of these 2 rays is the range of the original absolute value function.
Be careful! The inverse of an absolute value function is not a function, because for one |x| value there are 2 different |y| values.

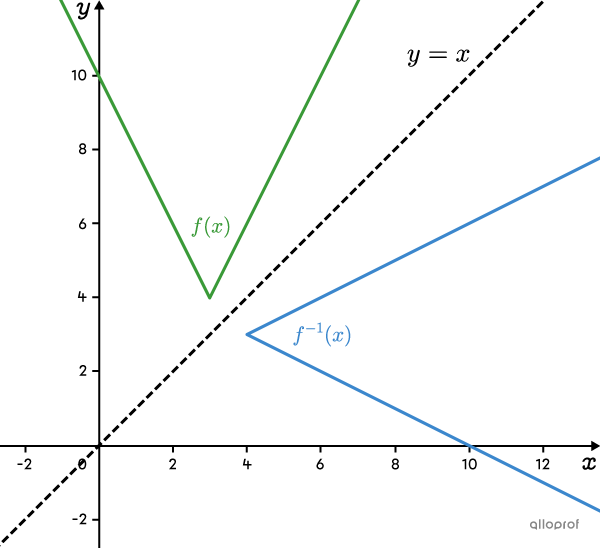
If the absolute value function opens upwards (when |a| is positive), its inverse opens to the right. In this case, |\text{range}(\color{#3a9a38}{f})=[k,+\infty[\;=\text{dom}(\color{#3b87cd}{f^{-1}}).|
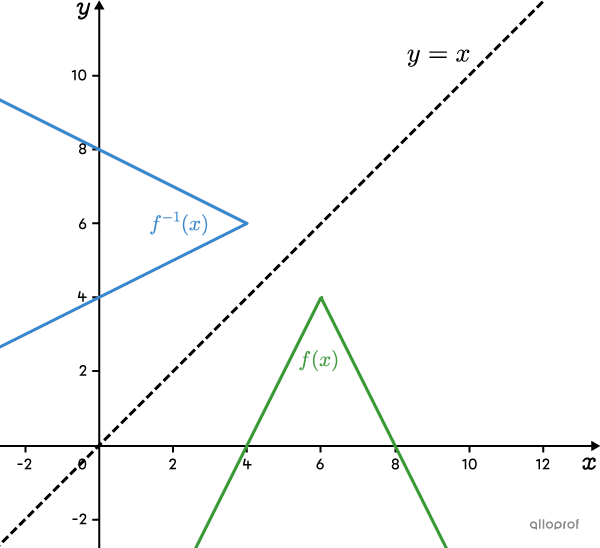
If the absolute value function opens downwards (when |a| is negative), its inverse opens to the left. In this case, |\text{range}(\color{#3a9a38}{f})=]-\infty,k]=\text{dom}(\color{#3b87cd}{f^{-1}}).|
Here are the steps to find the inverse of an absolute value function.
Switch |x| and |y.|
Isolate |y| to form 2 first degree equations.
Determine the domain of the inverse.
Find the rule for the inverse of the following function: |f(x).| ||f(x)=2\vert x-8\vert +2||
Switch |\boldsymbol{x}| and |\boldsymbol{y}|||\begin{align} \color{#3b87cd}{y}&=2\vert \color{#ff55c3}{x}-8\vert +2\\ \color{#ff55c3}{x}&=2\vert \color{#3b87cd}{y}-8\vert +2 \end{align}||
Isolate |\boldsymbol{y}| to form 2 first degree equations
Use the same approach as when we solve an equation containing an absolute value. First, isolate the absolute value bracket |\vert \color{#3b87cd}{y}-8\vert.| Next, apply the definition of the absolute value to form 2 equations, and then isolate |\color{#3b87cd}{y}| in each of these equations.||\begin{gather}\begin{aligned}x-2&=2\vert \color{#3b87cd}{y}-8\vert \\
\dfrac{x-2}{2} &= \vert \color{#3b87cd}{y}-8\vert \\
\dfrac{x}{2}-1 &= \vert \color{#3b87cd}{y}-8\vert \end{aligned}\\\Updownarrow\\ \overbrace{
\begin{aligned}
\dfrac{x}{2}-1&=\color{#3b87cd}{y}-8&\color{#ec0000}-\left(\dfrac{x}{2}-1\right)&=\color{#3b87cd}{y}-8\\
\dfrac{x}{2}+7&=\color{#333fb1}{y_1}&-\dfrac{x}{2}+1&=\color{#3b87cd}{y}-8\\
&&-\dfrac{x}{2}+9&=\color{#51b6c2}{y_2}
\end{aligned}} \end{gather}||So, the inverse of the absolute value function is 2 linear functions: |\color{#333fb1}{y_1}| and |\color{#51b6c2}{y_2}.|
The domain of these 2 lines must now be restricted to only contain the rays forming a V that opens to the correct side.
Determine the domain of the inverse
To do this, first determine the coordinates of the vertex of the original function and those of its inverse.
The vertex of |f(x)| is located at the point |(h,k)=(8,2).| To find the vertex of the inverse |f^{-1}(x),| swap the coordinates. This means the vertex of |f^{-1}(x)| is |(2,8).|
Since parameter |a| of |f(x)| is positive, the function opens upwards. So, the range of |f(x)| has the form |[k,+\infty[.| ||\text{range}(f)=[2,+\infty[.|| The range of |f(x)| becomes the domain of |f^{-1}(x).| ||\text{dom}(f^{-1})=[2,+\infty[.|| So, the inverse opens to the right.
Answer: The inverse of |\color{#3a9a38}{f(x)=2\vert x-8\vert +2}| has 2 rays: |\color{#333fb1}{y_1=\dfrac{x}{2}+7}| and |\color{#51b6c2}{y_2 = -\dfrac{x}{2}+9}| where |x\geq2.|
Here is the graph that shows|\color{#3a9a38}{f(x)}| as well as the two |(\color{#333fb1}{y_1}| and |\color{#51b6c2}{y_2})| rays that form its inverse.
Note: |f(x)| and its inverse are symmetric with respect to the axis |y=x.|

It is possible to graph the inverse of a function by swapping the |x| and |y| coordinates of some points. For example, here is the absolute value function |\color{#3a9a38}{f(x)}| graphed on the Cartesian plane.
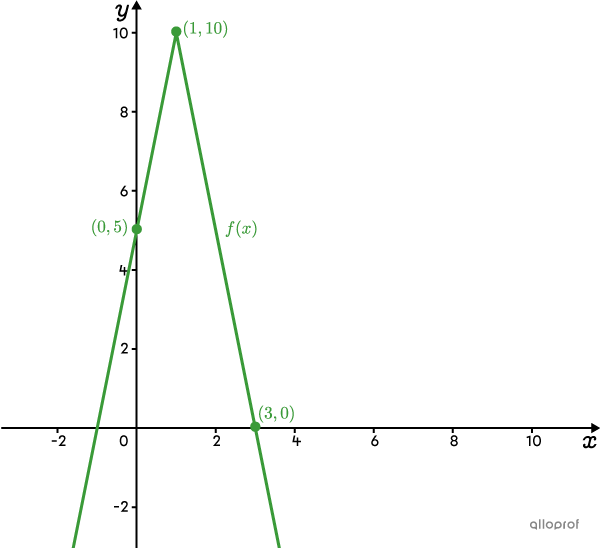
The vertex of |\color{#3a9a38}{f(x)}| becomes the vertex of |\color{#3b87cd}{f^{-1}(x)}.| ||\color{#3a9a38}{(1,10)}\ \rightarrow\ \color{#3b87cd}{(10,1)}||
The y-intercept of |\color{#3a9a38}{f(x)}| becomes a zero of |\color{#3b87cd}{f^{-1}(x)}.| ||\color{#3a9a38}{(0,5)}\ \rightarrow\ \color{#3b87cd}{(5,0)}||
A zero of |\color{#3a9a38}{f(x)}| becomes the initial y-intercept of |\color{#3b87cd}{f^{-1}(x)}.| ||\color{#3a9a38}{(3,0)}\ \rightarrow\ \color{#3b87cd}{(0,3)}.||
Since we now have the vertex and a point on each branch of the inverse, it is possible to graph |\color{#3b87cd}{f^{-1}(x)}.|
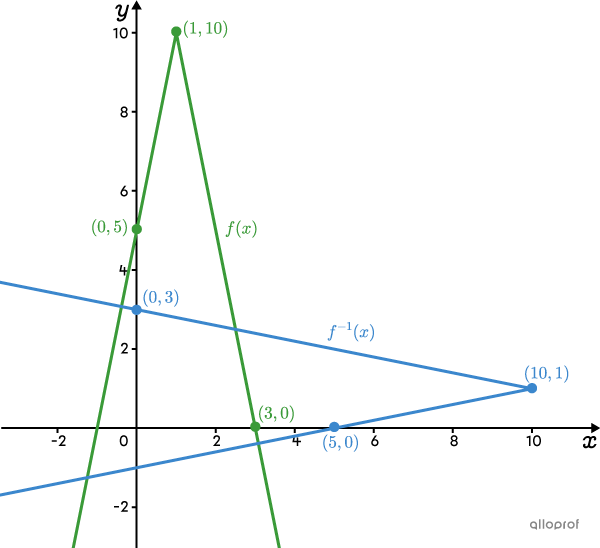
The rule of the 2 linear functions can also be found using 2 points.
The top branch gives the rule |y_1=-\dfrac{x}{5}+3| where |x\leq 10.|
The bottom branch gives the rule |y_2=\dfrac{x}{5}-1| where |x\leq 10.|