Matières
Niveaux
La fonction tangente
Fiche | Mathématiques
Secondaire
5
Lorsqu'on s'intéresse à la valeur de la pente de la droite qui relie le centre du cercle trigonométrique à un point précis du cercle trigonométrique, on utilise la fonction tangente.
En d'autres mots, |\tan\theta = \dfrac{\Delta y}{\Delta x} = \dfrac{\sin\theta}{\cos\theta}| où |\theta =| mesure de l'angle au centre du cercle trigonométrique.
-
Les équations des asymptotes sont |x=\dfrac{\pi}{2}+n\pi\ \text{où}\ n\in\mathbb{Z}.|
-
La période de la fonction tangente de base est de |\pi| radians.
-
Le point |(0,0)| est le point d'inflexion de la fonction.
- Le rôle des paramètres dans une fonction tangente
- Les propriétés de la fonction tangente
- Tracer une fonction tangente
- Trouver la règle d'une fonction tangente
- La réciproque de la fonction tangente (arctan)
- Résoudre une équation ou une inéquation tangente
- La résolution de problèmes impliquant la fonction tangente
La fonction tangente transformée
La fonction tangente sous la forme canonique s'écrit de la façon suivante : ||f(x)=a \tan\big(b(x-h)\big)+k||
où ||\begin{align}{\mid}b{\mid} &= \dfrac{\pi}{\text{période}} \\ h &= \text{Déphasage de la fonction} \\ k &= \text{Déplacement vertical de la fonction} \end{align}||
Remarques :
Le point |(h,k)| correspond au point d'inflexion de la fonction.
Les paramètres |a| et |b| sont différents de |0.|
Les paramètres de la fonction tangente
La période
La période est la distance qui sépare deux asymptotes consécutives.
On trouve la période de la fonction à partir de la formule suivante : ||p= \dfrac{\pi}{\mid b \mid}||
Ainsi, on peut trouver la valeur de |b| en l'isolant dans la formule ce qui donne : ||{\mid}b{\mid} = \dfrac{\pi}{p}||
Ensuite, on ajuste le signe de |b| en fonction de la variation de la courbe.
Le déphasage
Le déphasage est le déplacement horizontal du point d'origine |(0,0)| de la fonction de base. On le représente par la lettre |h| dans la fonction tangente sous la forme canonique. Les asymptotes se déplacent également de |h| unités.
Le paramètre |k|
Le paramètre |k| correspond au déplacement vertical du point d'origine |(0,0)| de la fonction de base.
Les asymptotes d'une fonction tangente
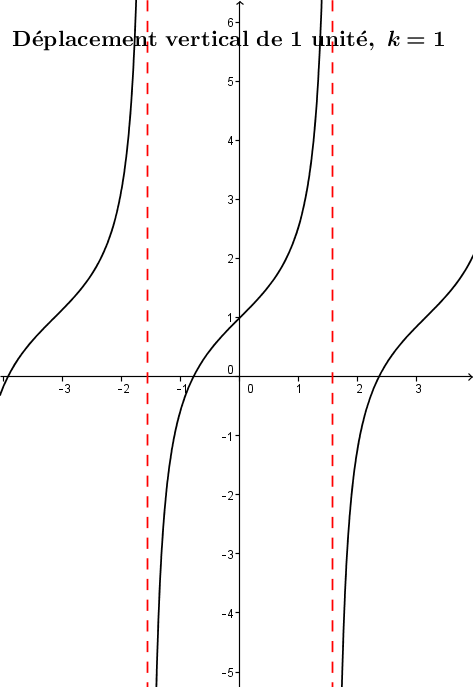
Les asymptotes de la fonction tangente sont des droites verticales. Comme la fonction tangente est une fonction périodique, le cycle (motif) se répète indéfiniment. Il y a donc une infinité d'asymptotes qui sont définies par une équation de la forme : |x = \left(h + \frac{p}{2}\right) + n p| où |n \in \mathbb{Z}| et |p| est la période de la fonction. La distance qui sépare les asymptotes vaut |p.|
