Matières
Niveaux
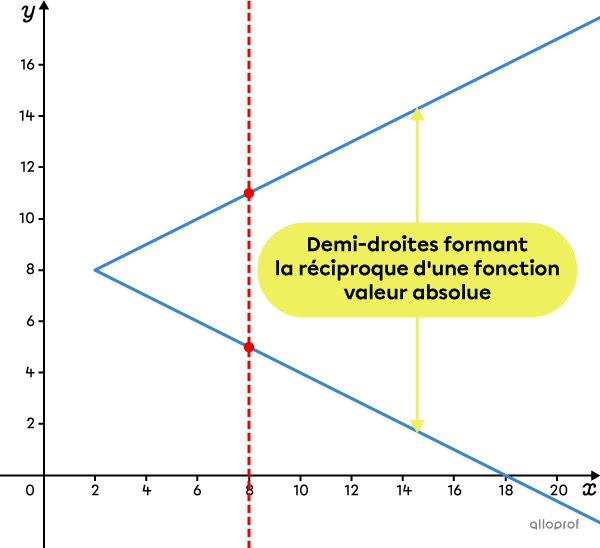
La réciproque d’une fonction valeur absolue est composée de 2 demi-droites qui débutent au même point et qui forment un V sur le côté. Le domaine de ces 2 demi-droites correspond à l’image de la fonction valeur absolue de départ.
Attention! La réciproque d’une fonction valeur absolue n’est pas une fonction, car pour une même valeur de |x,| il y a 2 valeurs différentes de |y.|
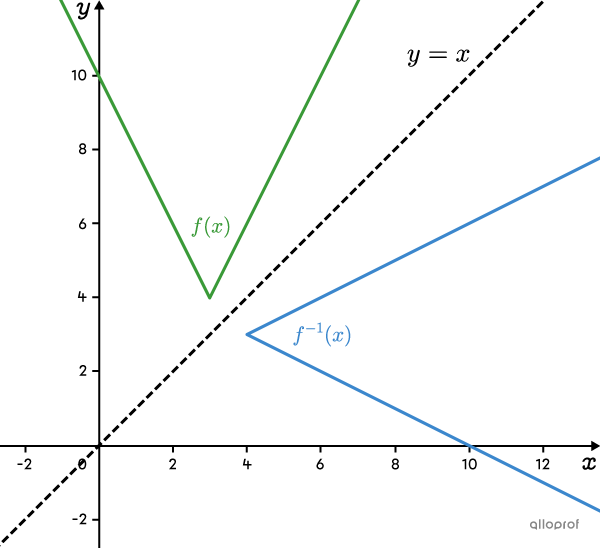
Si la fonction valeur absolue est ouverte vers le haut (lorsque |a| est positif), l’ouverture de sa réciproque est vers la droite. Dans ce cas, |\text{ima}(\color{#3a9a38}{f})=[k,+\infty[\;=\text{dom}(\color{#3b87cd}{f^{-1}}).|
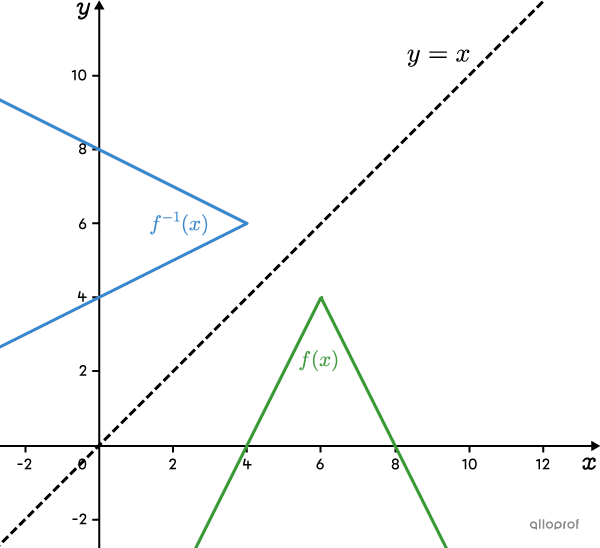
Si la fonction valeur absolue est ouverte vers le bas (lorsque |a| est négatif), l’ouverture de sa réciproque est vers la droite. Dans ce cas, |\text{ima}(\color{#3a9a38}{f})=\;]-\infty,k]=\text{dom}(\color{#3b87cd}{f^{-1}}).|
Voici les étapes à suivre pour trouver la réciproque d’une fonction valeur absolue.
Interchanger |x| et |y.|
Isoler |y,| afin de former 2 équations de degré 1.
Déterminer le domaine de la réciproque.
Donne la règle de la réciproque de la fonction |f(x)| suivante. ||f(x)=2\vert x-8\vert +2||
Interchanger |\boldsymbol{x}| et |\boldsymbol{y}| ||\begin{align} \color{#3b87cd}{y}&=2\vert \color{#ff55c3}{x}-8\vert +2\\ \color{#ff55c3}{x}&=2\vert \color{#3b87cd}{y}-8\vert +2 \end{align}||
Isoler |\boldsymbol{y,}| afin de former 2 équations de degré 1
Il faut faire la même démarche que lorsqu’on veut résoudre une équation contenant une valeur absolue. D’abord, on isole la valeur absolue |\vert \color{#3b87cd}{y}-8\vert.| Ensuite, on applique la définition de la valeur absolue pour former 2 équations, puis on isole |\color{#3b87cd}{y}| dans chacune de ces équations.||\begin{gather}\begin{aligned}x-2&=2\vert \color{#3b87cd}{y}-8\vert \\
\dfrac{x-2}{2} &= \vert \color{#3b87cd}{y}-8\vert \\
\dfrac{x}{2}-1 &= \vert \color{#3b87cd}{y}-8\vert \end{aligned}\\\Updownarrow\\ \overbrace{
\begin{aligned}
\dfrac{x}{2}-1&=\color{#3b87cd}{y}-8&\color{#ec0000}-\left(\dfrac{x}{2}-1\right)&=\color{#3b87cd}{y}-8\\
\dfrac{x}{2}+7&=\color{#333fb1}{y_1}&-\dfrac{x}{2}+1&=\color{#3b87cd}{y}-8\\
&&-\dfrac{x}{2}+9&=\color{#51b6c2}{y_2}
\end{aligned}} \end{gather}||Ainsi, la réciproque de la fonction valeur absolue est constituée de 2 fonctions affines : |\color{#333fb1}{y_1}| et |\color{#51b6c2}{y_2}.|
On doit maintenant restreindre le domaine de ces 2 droites pour obtenir les demi-droites permettant de former un V ouvert du bon côté.
Déterminer le domaine de la réciproque
Pour y arriver, il faut d’abord déterminer les coordonnées du sommet de la fonction de départ et celles de sa réciproque.
Le sommet de |f(x)| est situé au point |(h,k)=(8,2).| Pour trouver celui de la réciproque |f^{-1}(x),| on interchange les coordonnées. Ainsi, le sommet de |f^{-1}(x)| est |(2,8).|
Comme le paramètre |a| de |f(x)| est positif, la fonction est ouverte vers le haut. L’image de |f(x)| est donc de la forme |[k,+\infty[.| ||\text{ima}(f)=[2,+\infty[||L’image de |f(x)| devient le domaine de |f^{-1}(x).| ||\text{dom}(f^{-1})=[2,+\infty[||Ainsi, la réciproque est ouverte vers la droite.
Réponse : La réciproque de |\color{#3a9a38}{f(x)=2\vert x-8\vert +2}| est composée de 2 demi-droites : |\color{#333fb1}{y_1=\dfrac{x}{2}+7}| et |\color{#51b6c2}{y_2 = -\dfrac{x}{2}+9}| où |x\geq2.|
Voici le graphique qui montre |\color{#3a9a38}{f(x)}| ainsi que les 2 demi-droites |(\color{#333fb1}{y_1}| et |\color{#51b6c2}{y_2})| qui forment sa réciproque.
Remarque : |f(x)| et sa réciproque sont symétriques par rapport à l’axe |y=x.|

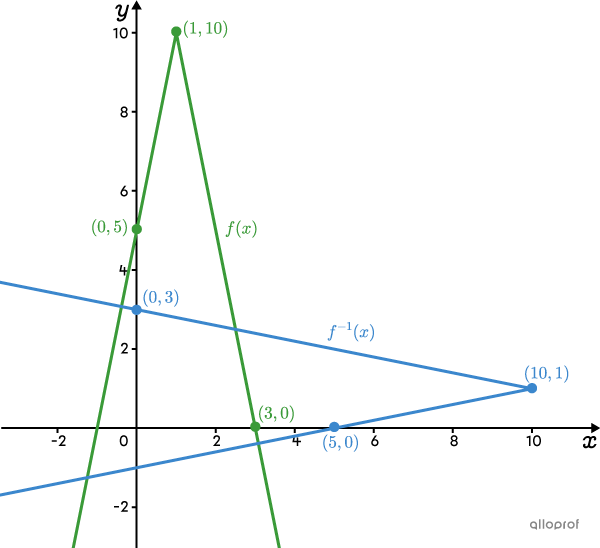
Il est possible de tracer la réciproque d’une fonction en interchangeant les coordonnées |x| et |y| de certains points. Par exemple, on a la fonction valeur absolue |\color{#3a9a38}{f(x)}| représentée dans le plan cartésien suivant.
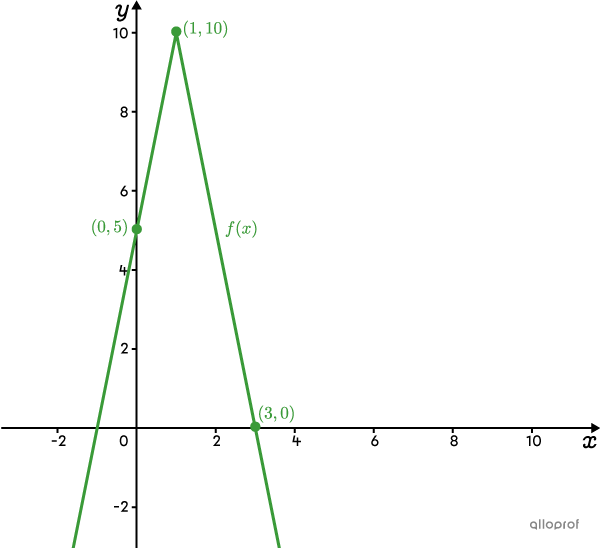
Le sommet de |\color{#3a9a38}{f(x)}| devient le sommet de |\color{#3b87cd}{f^{-1}(x)}.| ||\color{#3a9a38}{(1,10)}\ \rightarrow\ \color{#3b87cd}{(10,1)}||
L’ordonnée à l’origine de |\color{#3a9a38}{f(x)}| devient un zéro de |\color{#3b87cd}{f^{-1}(x)}.| ||\color{#3a9a38}{(0,5)}\ \rightarrow\ \color{#3b87cd}{(5,0)}||
Un zéro de |\color{#3a9a38}{f(x)}| devient une ordonnée à l’origine de |\color{#3b87cd}{f^{-1}(x)}.| ||\color{#3a9a38}{(3,0)}\ \rightarrow\ \color{#3b87cd}{(0,3)}||
Comme on connait le sommet et un point sur chacune des branches de la réciproque, on peut tracer |\color{#3b87cd}{f^{-1}(x)}.|
On peut aussi déterminer la règle des 2 fonctions affines à l’aide de 2 points.
Pour la branche du haut, on obtient |y_1=-\dfrac{x}{5}+3| où |x\leq 10.|
Pour la branche du bas, on obtient |y_2=\dfrac{x}{5}-1| où |x\leq 10.|