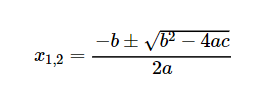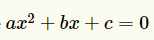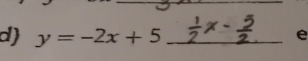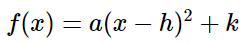Best Of

Bonjour CigogneLibvre4386

J'espère t'aider avec ta question

Voici une explication:

En algèbre, un monôme est un polynôme dont un seul coefficient est non nul. Autrement dit, c'est un polynôme particulier qui s'exprime sous la forme d'un produit d'indéterminées (notées X, Y…) affecté d'un coefficient. sont des monômes en une indéterminée.

Bonne Soirée

MandarineOrange9832

Salut :D

Pour le lettres f), g) et h), il faut trouver le taux de variation.

Un taux de variation est souvent /h, /s, etc. Il faut effectuer une division afin de le trouver lorsqu'on a un nombre de mètres par une période de temps. On veut un taux unitaire, c'est-à-dire combien de mètre pour 1 seule h (/h).

Pour le f), c'est 90m^2/4h.

Pour le g), c'est 165$/4semaines.

Pour le h), c'est 7km/1,75h (on a transformé le 45 minutes en heures).

Tu trouveras des unités de mesures pour la taux de variation de, respectivement, m^2/h, $/semaine et km/h.

N'hésite pas si tu as d'autres questions :D À bientôt :)

Salut !

Tout d'abord, il faut arriver à décortiquer les informations de l'énoncé en valeurs réelles. Tu peux déjà projeter quelques segments qui pourraient t'aider en connaissant la valeur du rayon :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Les lignes rouges ont une mesure de 8 cm.

Puis, vient la partie sur le produit des segments. Ici on t'indique que les deux cordes en se croisant produisent un totale de quatre segments : AE, BE, CE, DE. Ainsi, pour une seule corde, le produit des segments est 26cm. Par exemple, pour AB, le produit de AE et BE est 26. Tu as plusieurs possibilités : \(2 \times 13\), \(4 \times 6,5\).

Tu peux essayer avec 4 cm et 6,5 cm par exemple. J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !

Bonne journée !

Salut!

Tu as fait une petite erreur ici :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

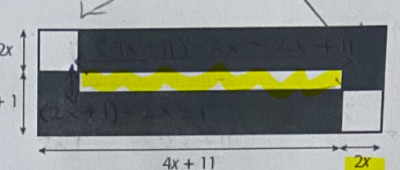
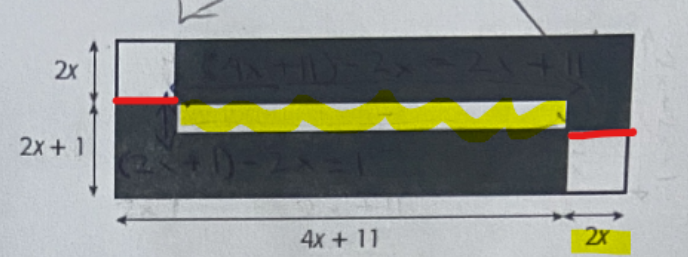
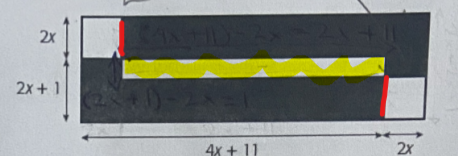
Tu as oublié d'ajouter le 2x à la mesure de la base du grand rectangle.

Ensuite, tu dois soustraire de l'aire du grand rectangle l'aire de la partie blanche, donc l'aire des deux carrés blancs ainsi que l'aire du petit rectangle blanc au centre.

Ceci est donc bon :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

mais il te reste à trouver l'aire de cette partie :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Indice, la base de ce petit rectangle blanc serait le résultat de (4x+11)-2x-2x :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Et sa hauteur serait le résultat de ((2x+1)+(2x))-(2x)-(2x)

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Si tu as d'autres questions, n'hésite pas à nous réécrire! :)

Coucou!

Malheureusement, il n'y a aucune autre façon de résoudre cette équation sans utiliser la formule quadratique, la factorisation ou la complétion du carré :(

Il n'est pas possible de faire une racine carrée sur un seul terme d'un côté de l'égalité. En d'autres mots, ceci serait faux :

$$ \sqrt{313,62}=\sqrt{8x^2} + 3x $$

Tandis que ceci serait possible :

$$ \sqrt{313,62}=\sqrt{8x^2+3} $$

mais cela ne nous avance pas, puisque l'expression \(\sqrt{8x^2+3} \) ne peut pas être simplifiée.

Je te conseillerais d'utiliser la formule quadratique, il se peut qu'il s'agisse d'une notion que tu apprendras plus tard cette année. Sinon, tu peux en faire part à ton professeur et l'informer qu'il s'agit d'un exercice qui n'est pas de niveau CST.

Voici comment utiliser la formule quadratique :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Tu dois ramener ton équation sous la forme :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

c'est-à-dire faire en sorte qu'un des deux côtés de l'égalité soit 0. Notre équation sera alors :

$$ 0=8x^2+3x-313,62$$

Nous pouvons alors identifier les paramètres a, b et c qui seront utilisés dans notre formule :

$$ a =8$$

$$ b =3$$

$$c=-313,62$$

Puis, nous devons insérer ces valeurs dans la formule, ce qui nous donne :

$$ x_{1,2} = \frac{-(3)±\sqrt{(3)^2-4(8)(-313,62)}}{2(8)} $$

Il ne reste plus qu'à effectuer le calcul :

$$ x_{1,2} = \frac{-3±\sqrt{9-4(8)(-313,62)}}{16} $$

$$ x_{1,2} = \frac{-3±\sqrt{9+10035.84}}{16} $$

$$ x_{1,2} = \frac{-3±\sqrt{10044.84}}{16} $$

$$ x_{1,2} = \frac{-3±100,22}{16} $$

À cette étape, nous devons diviser notre équation en deux, nous aurons une équation où le symbole séparant les deux termes sera un plus, et une autre où ce sera un moins :

$$ x_{1} = \frac{-3+100,22}{16} $$

et

$$ x_{2} = \frac{-3-100,22}{16} $$

Nous devons ensuite résoudre chacune de ces équations. La première :

$$ x_{1} = \frac{-3+100,22}{16} $$

$$ x_{1} = \frac{97,22}{16} $$

$$ x_{1} =6,076 $$

La deuxième :

$$ x_{2} = \frac{-3-100,22}{16} $$

$$ x_{2} = \frac{-103,22}{16} $$

$$ x_{2} = -6,45 $$

Nous trouvons ainsi que nous avons deux valeurs possibles de x qui satisfasse notre équation. Or, puisque la mesure d'un côté d'une figure ne peut pas être une valeur négatif, nous allons donc rejeter \( x_{2} = -6,45\). La réponse finale serait donc \( x =6,076 \).

Il se peut que tu trouves cela un peu compliqué si c'est la première fois que tu utilises la formule quadratique, ne t'inquiète pas, c'est normal! Avec un peu de pratique, tu verras que c'est assez simple finalement, malgré l'allure un peu effrayante de la formule ;)

J'espère que cela t'aide!

Pourtant tu as bien posé tous les éléments du problème.

Tu as trouvé que l'aire du terrain A est 156.81 m² (c'est le bon résultat mais tu as indiqué cm² par endroits)

le coût en a) est donc 65$/m² · 156.81 m² = 10192.65$

Pour trouver x en b) tu sais que l'aire

(2x+x)x/2 = 156.81 m²

3x·x = 313.62

x² = 313.62/3 = 104.54 => x = 10.22 m

• Je ne suis pas sûre de comprendre ta question/ ton problème.
• Tu nous donnes le corrigé mais on a pas les questions.
• Une fraction est plus précise: 6/7 est plus précis que 0.857... écourté à 0.86

Salut!

Testons-le pour voir! :)

$$ y=\frac{5}{x} $$

devient :

$$ x=\frac{5}{y} $$

On déplace la variable y à la position du numérateur :

$$ x\times y=\frac{5}{y} \times y$$

$$ x\times y=5$$

On élimine la variable x du côté du y :

$$ \frac{x\times y}{x}=\frac{5}{x}$$

$$ y=\frac{5}{x}$$

Donc, oui, tu avais bien raison! :D Cependant, je te conseille de toujours effectuer le calcul, tu auras moins de chance de faire des erreurs que si tu fais le calcul dans ta tête ;)

De plus, tu as une petite erreur de signes au numéro d).

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

$$ y=-2x+5$$

devient :

$$ x=-2y+5$$

Puis on isole y. On déplace la constante 5 :

$$ x-5=-2y+5-5$$

$$ x-5=-2y$$

On élimine le coefficient -2 de la variable y :

$$ \frac{x-5}{-2}=\frac{-2y}{-2}$$

$$ y=\frac{x}{-2}+\frac{-5}{-2}$$

La réponse est donc :

$$ y=-\frac{x}{2}+\frac{5}{2}$$

Si tu as d'autres questions, n'hésite pas à nous réécrire! :)

Salut!

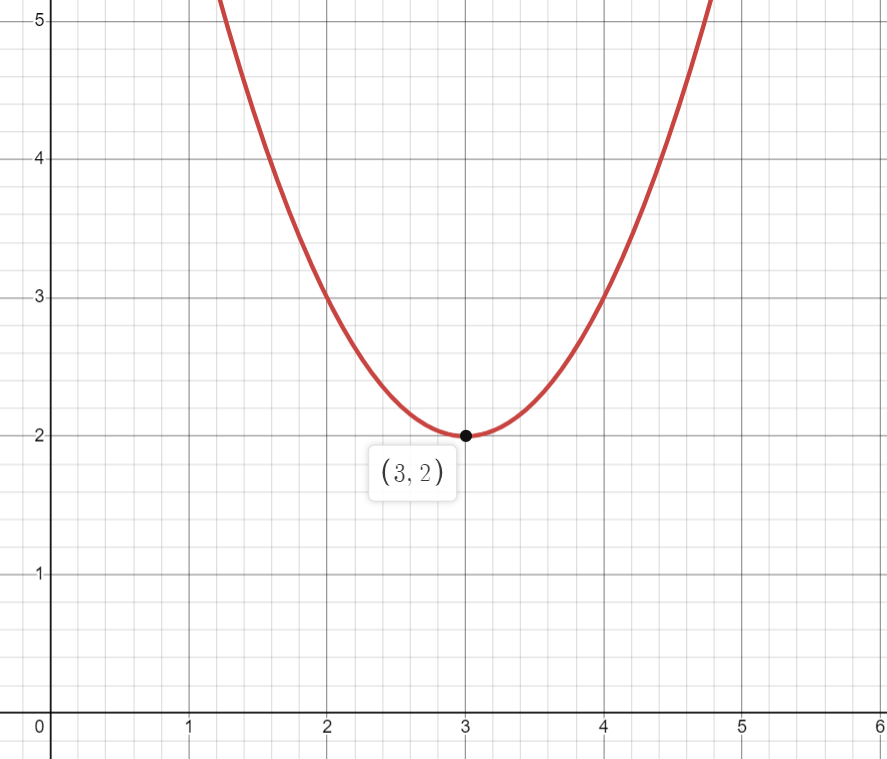
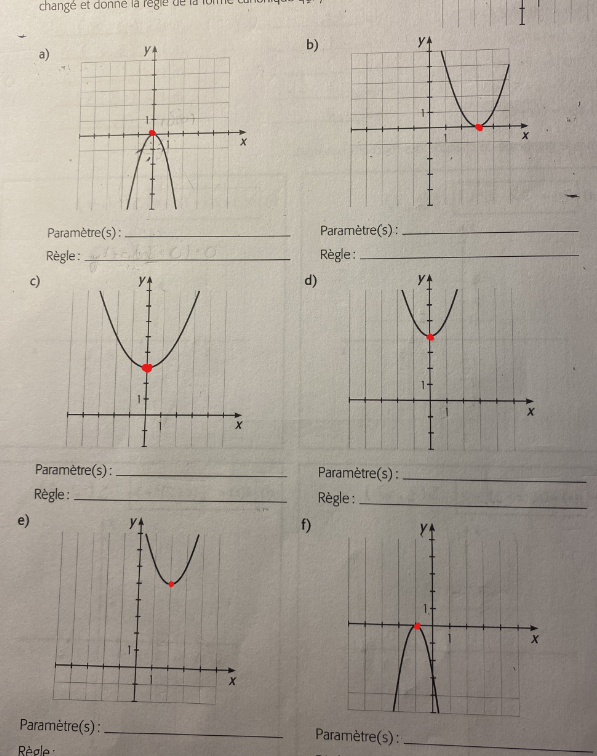
Pour chaque fonction, tu dois trouver la règle qui a la forme suivante :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

où h et k sont les sommets de la parabole.

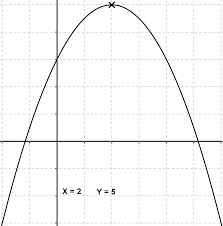
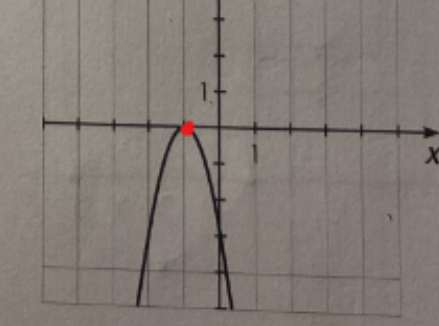
Si la parabole est ouverte vers le bas, son sommet est le point le plus en haut, comme ceci :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

tandis que si la parabole est ouverte vers le haut, son sommet est le point le plus en bas :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ainsi, les coordonnées de ce sommet te donneront la valeur des paramètres h et k.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

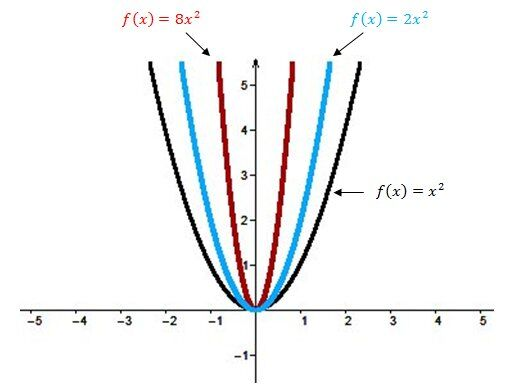
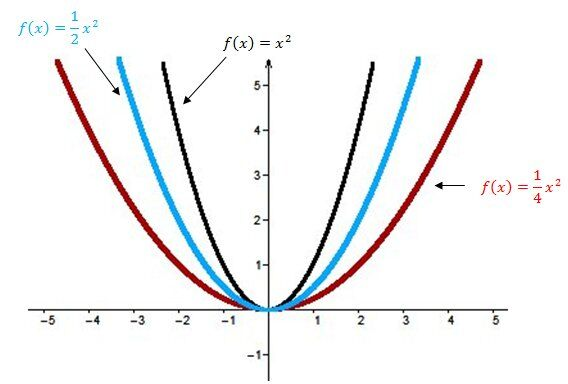
Le paramètre \(a\) influence la grandeur de l'ouverture de la parabole :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

tandis que son signe permet de déterminer si la parabole est ouverte vers le haut ou vers le bas.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Donc, pour toutes les fonctions qui sont ouvertes vers le bas, tu sais que le paramètre a est négatif.

Pour déterminer la valeur absolue du paramètre (la valeur de a, sans prendre en compte son signe), tu peux y aller approximativement. Par exemple, pour le numéro f, l'ouverture est visiblement plus petite que celle de la fonction de base f(x)=x². Ainsi, cela veut dire que la valeur absolue de \(a\) est supérieure à 1.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Voici des fiches sur cette notion qui pourraient t'être utiles :

• Trouver la règle d'une fonction polynomiale de degré 2 | Secondaire | Alloprof
• Le rôle des paramètres dans une fonction polynomiale de degré 2 | Secondaire | Alloprof

Si tu as d'autres questions, n'hésite pas à nous réécrire! :)