Best Of
Re: Question
Bonsoir DagobahLambda4401,
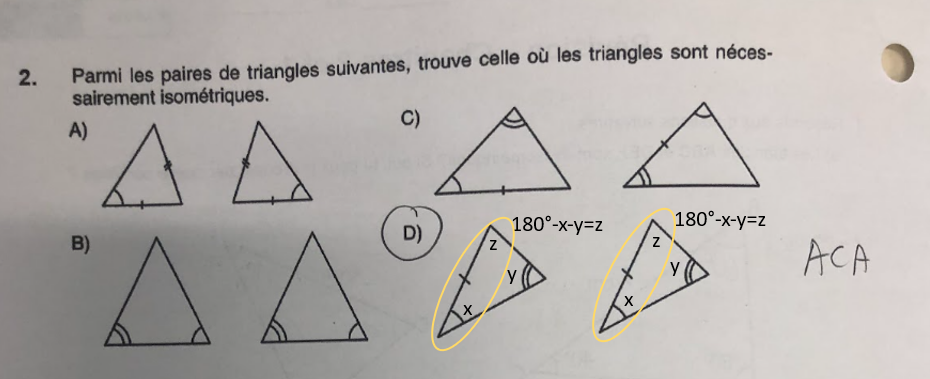
Il est vrai que sans analyser la situation, nous ne pouvons pas directement affirmer que ce sont des triangles isométriques. Cependant, tu peux argumenter pour en tirer cette conclusion.
Les deux angles isométriques et le côté sont situés exactement aux mêmes endroits. Ainsi, il est clair que l'angle restant sera isométrique aussi. En effet, la somme des angles intérieurs est de 180°. Maintenant, tu as la condition ACA.
N'hésite pas à nous contacter si tu as d'autres questions!
Re: Question
Salut !
Pour bien comparer les valeurs qu'on te donne, il est utile de les placer sur le même dénominateur :
Ainsi, tu dois commencer par trouver le plus petit commun multiple. Je te laisse essayer par toi-même et si tu as d'autres questions, n'hésite pas !
Re: Question
Bonjour ElfeArtistique5108,
Merci d’utiliser la zone d’entraide pour te venir en aide.
Ne tinquiète pas on va pouvoir taider.
D’abord, je crois que cette fiche d’Alloprof pourrait être un bon début pour te donner des trucs qui te permettront de comprendre la différence entre une molécule et un atome.
N’hésites surtout pas à revenir nous voir si tu as plus de questions, on est toujours prêt à t'aider,
OlorotitanTurbo2685
Re: Question
Bonjour CobraAgile,
Merci pour ta question!
Je ne peux malheureusement pas te donner directement la réponse à tes exercices. Je t'invite à essayer de les résoudre, et à m'écrire avec une question plus précise! Il me sera alors plus facile de t'aider.
Kylan
Re: Question
Salut ElfeArtistique5108!
Merci d'avoir posé une question sur la zone d'entraide.
Pour te répondre, un atome est l'élément de base d'une molécule, une molécule est formé d'au moins 2 atomes!
Je t'invite à voir cette fiche concernant les molécule : https://www.alloprof.qc.ca/fr/eleves/bv/sciences/la-molecule-s1575
J'espère t'avoir aidé, n'hésite pas de reposer des questions,
On croit tous en toi!
-LuneTurquoise4340
Re: Question
Bonjour ElfeArtistique5108
Merci d'avoir utilisé la zone d'entraide Alloprof. Je suis là pour te guider à la réponse à ta question.
Tout d'abord, l'atome est un élément présent dans le tableau périodique, tandis que la molécule est liaison chimique de deux atomes ou plus.
Voici quelques fiches qui t'aideront à comprendre la différence entre les deux:
- L'atome: https://www.alloprof.qc.ca/fr/eleves/bv/sciences/l-atome-s1574
- La molécule: https://www.alloprof.qc.ca/fr/eleves/bv/sciences/la-molecule-s1575
J'espère que je t'ai aidé à répondre à ta question,
N'hésite pas à nous poser de nouvelles questions,
Bon courage,
RobotDelta7259
Re: Question
Merci pour ta question!
Un atome est la plus petite particule de la matière qu'on peut obtenir par des moyens chimiques dont des échanges d'électron. C'est l'unité de base de la molécule.
Une molécule est une particule formée de deux atomes ou plus.
Ainsi, la différence entre un atome et une molécule réside dans le nombre d'atomes qu'ils contiennent.
Cette fiche du site d'Alloprof distingue les atomes et les molécules :
N'hésite pas si tu as d'autres questions!
Re: Question
Bonjour ElfeArtistique5108,
Merci d’utiliser la zone d’entraide pour te venir en aide.
C’est tout à fait normal d’avoir un peu de difficulté, je vais pouvoir te guider.
D’abord, je crois que cette fiche d’Alloprof pourrait être un bon début pour te donner des trucs qui te permettront de comprendre comment calculer le périmètre d'une figure rapidement et efficacement. Mais pour le faire tu peux additionner tous les cotés de la figure
N’hésites surtout pas à revenir nous voir si tu as des questions,
Bon travail,
TortueComique679
Re: Question
Bonjour LokoriSuperbe7793,
Pour résoudre ce type d'exercice, je te suggère de faire le graphique des deux fonctions valeurs absolues dans un plan cartésien et de trouver le point d'intersection de ces deux fonctions. Cela te permettra d'avoir la solution à cette équation.
Re: Question
Salut!
Tu dois séparer l'équation en cas possibles en appliquant la définition de la valeur absolue.
L'équation |x-7|=|x+5| devient :
$$x-7=-(x+5)$$
$$ou$$
$$x-7=x+5$$
$$ou$$
$$-(x-7)=x+5$$
$$ou$$
$$-(x-7)=-(x+5)$$
Les deux derniers cas sont identiques aux deux premiers, on peut donc les éliminer et résoudre uniquement les deux premiers (Si les deux côtés ont des signes négatifs, ceux-ci s'éliminent. Le cas 4 devient donc le cas 2. Si un seul des deux côtés a un signe négatif, alors on peut déplacer ce signe de n'importe quel côté de l'équation. Le cas 3 équivaut donc au cas 1).
Ainsi, on a :
$$x-7=-(x+5)$$
$$ou$$
$$x-7=x+5$$
Il n'y a pas de solution pour le second cas :
$$x-7=x+5$$
$$x-7-x=x+5-x$$
$$-7=5$$
Ce qui est faux (on a deux droites parallèles de pente 1 qui n'ont aucun point d'intersection, d'où le fait qu'on ne peut pas résoudre cette équation).
Il nous reste donc à résoudre le premier cas, soit :
$$x-7=-(x+5)$$
$$x-7=-x-5$$
$$x-7+x=-x-5+x$$
$$2x-7=-5$$
$$2x-7+7=-5+7$$
$$2x=2$$
$$\frac{2x}{2}=\frac{2}{2}$$
$$ x = 1$$
Voilà! :) Voici une fiche sur cette notion qui pourrait t'être utile : Résoudre une équation ou une inéquation contenant une valeur absolue | Secondaire | Alloprof
Si tu as d'autres questions, n'hésite pas à nous réécrire! :)