Subjects
Grades
Here is a brief study guide containing all the concepts covered in the Secondary 4 SN mathematics pathway. To explain everything, each formula will be followed by an example and a link to a concept sheet in our virtual library.
Dividing polynomials is done the same way as dividing two numbers using long division.
Find the result of the following division:
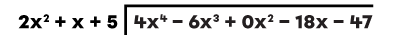
You can follow the steps below to add or subtract rational expressions:
Factor the numerator and denominator of each fraction.
Establish all of the restrictions (denominators other than 0).
If possible, cancel the common factors in each of the fractions.
Find a common denominator.
Complete the addition or subtraction with the numerator.
If possible, simplify the final rational expression by factoring the numerator and denominator.
Simplify the following algebraic expression:
|\displaystyle \frac{x-2}{x+5} - \frac{3}{-3x-12}|
It is important to master the concept of distributivity associated with multiplication:
If possible, simplify expressions in brackets.
Distribute each of the terms in the first bracket over all the terms in the second bracket.
Simplify by adding and subtracting like terms.
Find the simplified algebraic expression for the following multiplication: ||(7x+4)(2x^2-4x+3)||
Sometimes several factorization methods are required to factor an algebraic expression. As a result, it is important to master all of them.
|
EXAMPLE OF THE PRODUCT-SUM METHOD |
|
|---|---|
|
What measurements (in numerical form or as an algebraic expression) can be associated with each of the dimensions of a rectangular prism whose volume is |4x^2+8x−32\ \text{cm}^3|? |
|
|
CALCULATIONS |
EXPLANATIONS |
|
|\begin{align} &4x^2+8x−32 \\ =\ &4(x^2+2x−8)\end{align}| |
If possible, factor out the greatest common factor, making sure that all coefficients remain whole numbers. |
|
|\begin{align} &4(\color{blue}{x^2}+\color{red}{2x}\color{green}{−8}) \\\\ P =\ &\color{blue}{1}\times \color{green}{−8}=−8 \\ S =\ &\color{red}{2} \end{align}| The numbers are |4| and |−2,| because |4\times -2 = -8| and |4+-2=2.| |
Determine the numbers that correspond to the product and the sum of the polynomial in brackets. |
|
|\begin{align} &4(x^2+\color{red}{2x}−8) \\ |
Separate the |\color{red}{x}| term into two terms, using the two numbers found and factor using the grouping method. |
|
The three dimensions measurement are |4,| |(x+4)| and |(x−2)| cm. |
|
|
EXAMPLE OF A DIFFERENCE OF SQUARES |
|
|---|---|
|
What are the algebraic expressions that represent the measurement of the base and the height of a triangle whose area is |(2x^2 −8)\ \text{m}^2\ ?| |
|
|
CALCULATIONS |
EXPLANATIONS |
|
|\begin{align} \frac{\color{blue}{b}\times \color{red}{h}}{2} &= 2x^2 - 8 \\ \Rightarrow\ \color{blue}{b}\times \color{red}{h} &=4x^2 -16 \end{align}| |
Create the equation that represents the situation. |
|
|\begin{align} \sqrt{4x^2} &= 2x \\ \sqrt{16} &= 4 \end{align}| This is a subtraction between two terms. |
Verify that the binomial meets the criteria of a difference of squares. |
|
|\begin{align} \color{blue}{b} \times \color{red}{h} &= 4x^2 − 16 \\ \Rightarrow\ \color{blue}{b} \times \color{red}{h} &= \color{blue}{(2x−4)}\color{red}{(2x+4)} \end{align}| |
Factor according to this model: |a^2-b^2=(a-b)(a+b)| |
|
Therefore, we can conclude that |\color{blue}{b = (2x−4)}| and |\color{red}{h = (2x+4)}\ \text{m}.| |
|
|
EXAMPLE OF A PERFECT SQUARE TRINOMIAL |
|
|---|---|
|
What is the algebraic expression associated with the measurement of one side of a square that has an area of |\color{blue}{9}x^2 − \color{red}{42}x + \color{green}{49}\ \text{m}^2|? |
|
|
CALCULATIONS |
EXPLANATIONS |
|
|\begin{align} \sqrt{\color{blue}{a}} &= \sqrt{\color{blue}{9}} = \color{blue}{3} \\ \sqrt{\color{green}{c}} &= \sqrt{\color{green}{49}} = \color{green}{7} \\\\ \color{red}{c} &\overset{?}{=} 2\sqrt{\color{blue}{a}}\sqrt{\color{green}{c}} \\ \Rightarrow\ \color{red}{42} &= 2\times \color{blue}{3} \times \color{green}{7} \end{align}| |
Verify that the trinomial is indeed a perfect square trinomial. |
|
|\begin{align} &\color{blue}{9}x^2 − \color{red}{42}x + \color{green}{49} \\ =\ &(\color{blue}{3}x-\color{green}{7})^2 \end{align}| |
Factor according to the perfect square trinomial model. |
|
Since the area of a square is calculated using the formula |A=c^2,| we can deduce that |A=(\color{blue}{3}x-\color{green}{7})^2.| By association, we obtain |c=(\color{blue}{3}x-\color{green}{7})\ \text{m}.| |
|
|
EXAMPLE USING THE COMPLETING THE SQUARE METHOD |
|
|---|---|
|
Find the equation of this parabola in its factored form: ||f(x) = -3x^2 - \frac{1}{2}x + 6|| |
|
|
CALCULATIONS |
EXPLANATIONS |
|
|\begin{align} &\color{blue}{-3}x^2 - \dfrac{1}{2}x + 6 \\ =\ &\color{blue}{-3}\left(x^2 + \color{red}{\dfrac{1}{6}}x - 2\right) \end{align}| |
Factor out a common factor to ensure that the coefficient of the term in |x^2 = 1.| |
|
|\begin{align} &\left(\dfrac{\color{red}{b}}{2}\right)^2 \\ =\ &\left(\dfrac{\color{red}{\frac{1}{6}}}{2}\right)^2 \\ =\ &\color{green}{\frac{1}{144}} \end{align}| |
Calculate the value of |\left(\dfrac{\color{red}{b}}{2}\right)^2|. |
|
|\begin{align} &-3\left(x^2 + \frac{1}{6}x \color{green}{+ \frac{1}{144} - \frac{1}{144}} - 2\right) \\ = &-3 \left(\left[x^2 + \frac{1}{6}x \color{green}{+ \frac{1}{144}}\right] \color{green}{- \frac{1}{144}} - 2\right) \\ = &-3 \left(\left[x + \frac{1}{12}\right]^2 - \frac{289}{144}\right) \end{align}| |
Add and then subtract this value to get a perfect square trinomial. |
|
|\begin{align} &-3 \left(\left[x + \frac{1}{12}\right]^2 - \frac{289}{144}\right) \\ = &-3 \left(\Big(x + \frac{1}{12} + \frac{17}{12}\Big)\Big(x + \frac{1}{12} - \frac{17}{12}\Big)\right) \\ = &-3 \left(x + \frac{18}{12}\right) \left(x - \frac{16}{12}\right) \\ = &-3 \left(x + \frac{3}{2}\right) \left(x - \frac{4}{3}\right) \end{align}| |
Factor using a difference of squares with the terms in brackets. |
|
The factored form of the starting equation is: |f(x) = -3 \left(x + \dfrac{3}{2}\right) \left(x - \dfrac{4}{3}\right).| |
|
|
EXAMPLE OF THE QUADRATIC FORMULA |
|
|---|---|
|
What are the algebraic expressions or measurements that can be associated with the measurements of the three dimensions of a rectangular prism whose volume is |(\color{blue}{3}x^2 + \color{green}{4}x \color{red}{- 8})\ \text{mm}^3|? |
|
|
CALCULATIONS |
EXPLANATIONS |
|
|\begin{align} &\dfrac{^-\color{green}{b} \pm \sqrt{\color{green}{b}^2 - 4 \color{blue}{a} \color{red}{c}}}{2 \color{blue}{a}} \\ =\ &\dfrac{^-\color{green}{4} \pm \sqrt{\color{green}{4}^2 - 4 (\color{blue}{3})(\color{red}{^-8})}}{2 (\color{blue}{3})} \end{align}| |
Apply the quadratic formula: |\dfrac{^-b \pm \sqrt{b^2 - 4ac}}{2a}| |
|
|\begin{align} &\dfrac{^-\color{green}{4} \pm \sqrt{\color{green}{4}^2 - 4 (\color{blue}{3})(\color{red}{^-8})}}{2 (\color{blue}{3})} \\ =\ &\dfrac{^-\color{green}{4} \pm \sqrt{112}}{2 (\color{blue}{3})} \end{align}| |
Simplify the radicand. |
|
|\begin{align} &\dfrac{^-\color{green}{4} \pm \sqrt{112}}{2 (\color{blue}{3})} \\\\ \Rightarrow x_1=\ &\dfrac{^-\color{green}{4} + \sqrt{112}}{2 (\color{blue}{3})} &&\text{et}\ x_2 = \dfrac{^-\color{green}{4} - \sqrt{112}}{2 (\color{blue}{3})} \\ \Rightarrow x_1 \approx\ &1{.}1 &&\text{et}\ x_2\ \approx ^-2{.}43 \end{align}| |
Identify the two possible answers. |
|
|\color{blue}{3}x^2 + \color{green}{4}x \color{red}{- 8}= 3(x-1{.}1)(x-^-2{.}43)| |
Write the factorization of the initial polynomial. |
|
Arbitrarily, the measurements of width, depth, and height of the prism can be associated with |3\ \text{mm},| |(x-1{.}1)\ \text{mm}| and |(x+2{.}43)\ \text{mm}.| |
|
Functional form (Standard form): |f(x) = a(x-h)^2 + k| where |(h,k)| is the coordinate of the vertex.
General form: |f(x) = ax^2 + bx + c|
Factored form: |f(x) = a (x - z_1) (x - z_2)| where |z_1| and |z_2| are the zeros of the parabola.
Use the information provided in the table below to determine the parabola’s equation in its three different forms.
For second-degree polynomial functions: |a \ne \dfrac{\Delta y}{\Delta x}|
A step function’s equation is written in the form ||f(x) = a \left[ b(x-h)\right] + k||
where
|(h,k) = | coordinates of a closed point
|{\mid}a{\mid} = | vertical distance or height between two steps and
|\dfrac{1}{\mid b \mid} = | length of a step
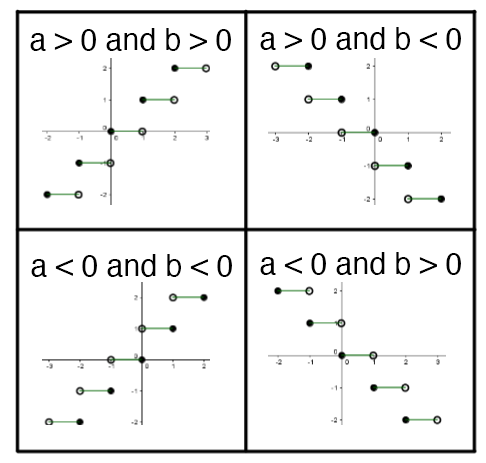
To determine the signs of |a| and |b,| we can refer to the direction of the open and closed points and the increasing or decreasing variation of the graph:
A grocery store has a new reward program that offers stamps for discounts on certain items.
Customers receive five stamps with a minimum purchase of $5. They receive seven more stamps for every additional $22 they spend.
Using this information, what interval corresponds to a customer's total bill if they receive 47 stamps from their purchase?
The inverse of function |f(x)|, denoted as |f^{-1}(x)|, is obtained by inverting the coordinates of the points such that |(x,y) \rightarrow (y,x)|
Sketch the inverse of the following function:
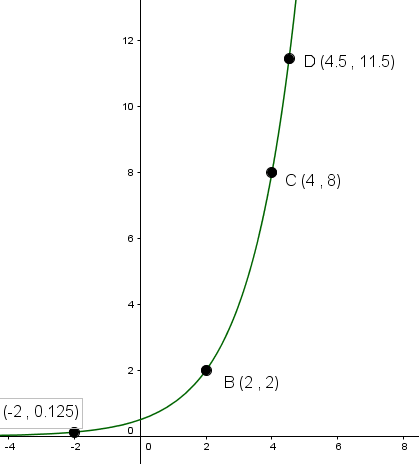
The inverse of a function is not always a function itself. In the cases studied here, these functions are inverses of each other:
Exponential and logarithmic functions;
A linear function with respect to itself;
A second-degree function (with a restricted domain) and a square root function.
The same criteria must always be analyzed when studying a function:
the domain: all possible values of |x|
the range: all possible values of |y|
the x-intercept (zeros): the value(s) of |x| when |y=0|
the y-intercept: the value of |y| when |x=0|
the maximum: the greatest value of |y|
the minimum: the smallest value of |y|
increasing: when the graph "goes upwards" or is constant
decreasing: when the graph "goes downwards" or is constant
positive sign: portion of the graph that is above or equal to the |x|-axi
negative sign: portion of the graph that is below or equal to the |x|-axis
As an accountant of a large company, you must give a detailed account of the trends in profits over the past year. To help, here is a graph of the last 12 months.
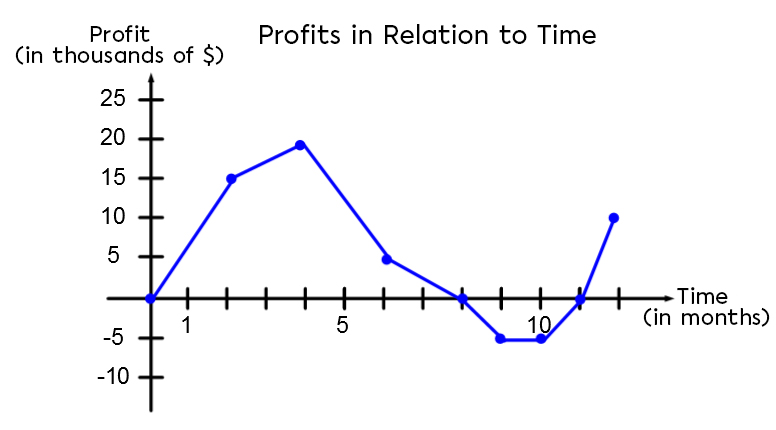
You must perform a complete study of this graph to prepare for your presentation speech and properly support your argument.
We can follow these steps to solve a system of equations:
Identify the variables related to the unknown values.
Create the equations according to the situation.
Use the appropriate method to solve this system (comparison, substitution, or reduction) according to the form of the equations found.
Substitute the value of the found variable into one of the starting equations to find the value of the other variable.
To respect the constraints imposed by the city, an entrepreneur must divide his wooded lot into two different rectangular lots.
Given that the area of the lots must be equivalent, determine the possible dimensions, in decametres, of these two lots.
Two figures are equivalent when they have the same area.
To make the cost of paving his new driveway the same as paving his old one, Julien wants the two driveways to be equivalent.
What should be the width of his new driveway?
Two solids are equivalent when they have the same volume.
A company that works with outdoor gear wants to offer two different tent models. To keep production costs the same, they want these two models to be equivalent.
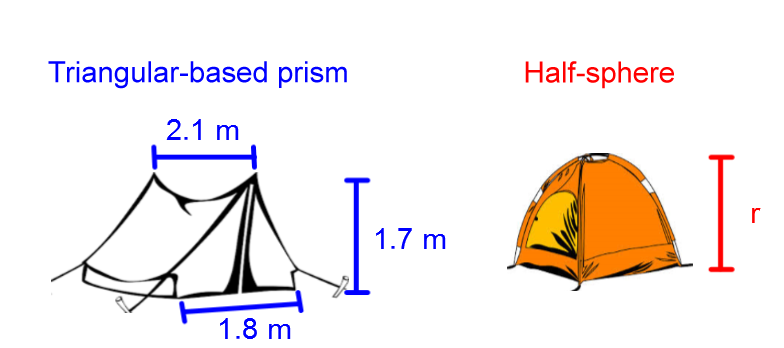
What must be the height of the second model for the tents to be equivalent?
Using the angle |\theta| as a reference, we have:
|\sin \theta = \dfrac{\text{Measure of the side opposite}\ \theta}{\text{Measure of the hypotenuse}}|
|\cos \theta = \dfrac{\text{Measure of the side adjacent}\ \theta}{\text{Measure of the hypotenuse}}|
|\tan \theta = \dfrac{\text{Measure of the side opposite} \ \theta}{\text{Measure of the side adjacent to} \ \theta}|
A house's roof trusses must have a minimum angle of elevation of |25^\circ| to meet building standards. To ensure that this constraint is respected, a manufacturer decides to establish this angle at |35^\circ.| If we know that the length of the roof truss is 13 metres, what are the measurements of the other two sides?
To determine the route a helicopter should take to pick up distressed people in the forest, a map of the region has been triangulated with the current locations of the helicopter, the hospital, and the people in distress.
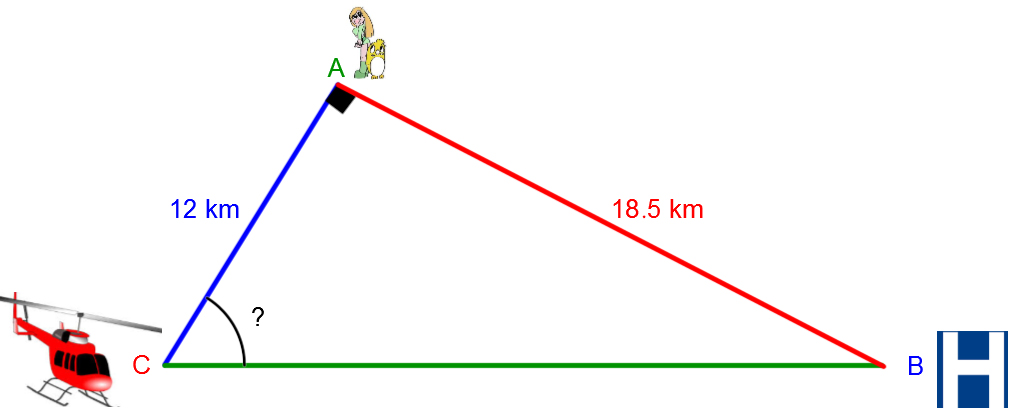
According to this drawing, what angle of orientation should the helicopter use to reach the people as quickly as possible?
A series of equivalences can be deduced for any given triangle.
|\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C}|
Horse races are sometimes organized during western festivities to liven up the events. During these races, cowboys must ride around each of three barrels, which are arranged in the shape of an isosceles triangle.
Using the measurements provided, what is the distance between each of the barrels?
To ensure maximum aerodynamics, the shape of some racing cars resembles a triangle.
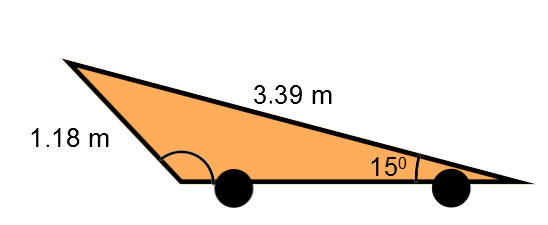
What should the angle closer to the back wheel measure for these proportions to be maintained?
When identifying triangles, it is always essential to identify
|\color{green}{\text{side a opposite to angle A}}|
|\color{red}{\text{side b opposite to angle B}}|
|\color{blue}{\text{side c opposite to angle C}}|
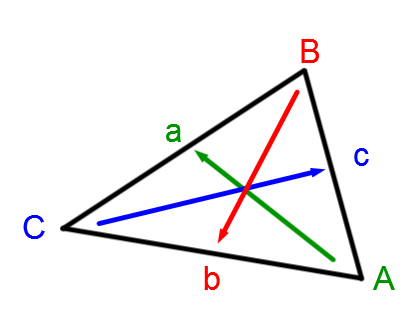
A series of equivalences can be deduced for any given triangle.
|a^2 = \color{blue}{b}^2 + \color{red}{c}^2 - 2 \color{blue}{b} \color{red}{c} \cos A|
|\color{blue}{b}^2 = a^2 + \color{red}{c}^2 - 2 a \color{red}{c} \cos \color{blue}{B}|
|\color{red}{c}^2 = a^2 + \color{blue}{b}^2 - 2 a \color{blue}{b} \cos \color{red}{C}|
A hunter, who uses a bow, settles in the corner of his land to maximize his chances of hunting a moose. The following triangle shows the range of his arrows:
Based on the information provided, what |\color{red}{\text{distance}}| can the moose walk while staying as far as possible from the hunter?
A bank is installing a rotating surveillance camera in its entrance hall to keep its employees safe. In addition, a security guard is in charge of monitoring the same area, defined by the following triangle:
What should the camera's rotation angle measure to ensure that there are no blind spots?
To achieve this, add lines (usually a height) with particular properties and unknown measures.
Choose the correct vertex from which to draw a height.
Use the trigonometric ratios in the right triangle to find the missing measurements.
Apply the formula for the area of a triangle with the found measurements.
Find the area of the following triangle:
A - S - A: Two triangles are congruent when a pair of corresponding congruent sides is located between two pairs of corresponding congruent angles.
S - A - S: Two triangles are congruent when a pair of corresponding congruent angles is located between two pairs of corresponding congruent sides.
S - S - S: Two triangles are congruent when all pairs of corresponding sides are congruent.
Due to machinery problems, construction workers need to complete the construction of a house by assembling the triangular-shaped roof trusses themselves. All of the trusses must be identical.
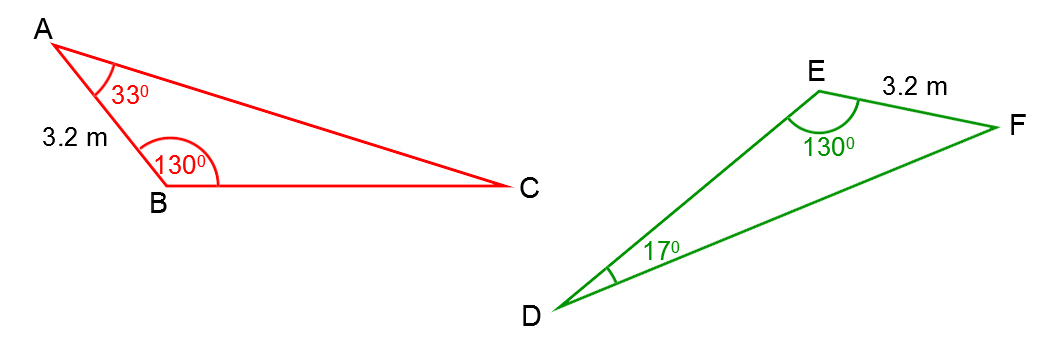
With the information provided above, demonstrate that these two constructions are congruent.
A - A: Two triangles are similar when two pairs of corresponding angles are congruent.
S - A - S: Two triangles are similar when a pair of corresponding congruent angles is located between two pairs of proportional corresponding sides.
S - S - S: Two triangles are similar if all three pairs of corresponding sides are proportional.
The city is organizing a family run as part of a fundraiser for a community organization. They want the adults to take a path similar to that of the children.
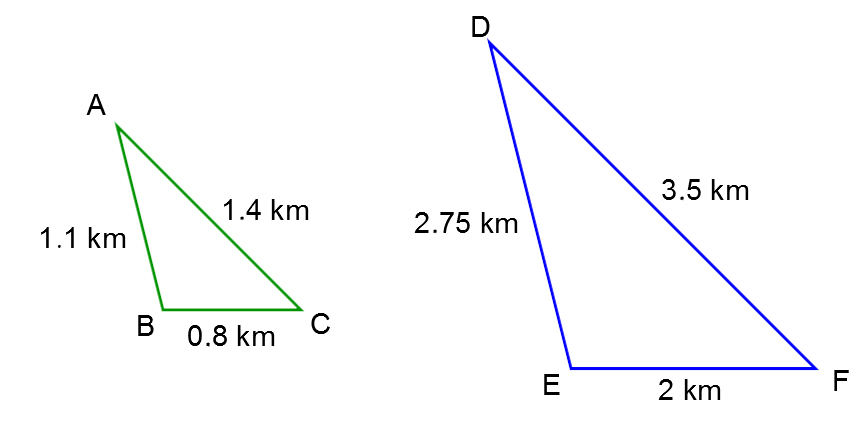
Taking into account the information provided, demonstrate that the two paths are similar.
From the following right-angled triangle, we can deduce three theorems from the following right-angled triangle.
In a right triangle, the measurement of each side of the right angle is the geometric mean between its projection onto the hypotenuse and the hypotenuse itself.||\begin{align} \dfrac{m}{a} = \dfrac{a}{c}\ &\Leftrightarrow\ a^2 = m c \\\\ \dfrac{n}{b} = \dfrac{b}{c}\ &\Leftrightarrow\ b^2 = n c \end{align}||
In a right triangle, the height measurement (altitude) is the geometric mean of the projections of the sides onto the hypotenuse. ||\dfrac{m}{h} = \dfrac{h}{n}\ \Leftrightarrow\ h^2 = m n||
In a right triangle, the product of the measurements of the hypotenuse and the height (altitude) equal the product of the measurements of the sides of the right angle. ||c h = a b||
To stand out from other contractors, a construction company suggests houses with roofs of different shapes. Among these choices, we have the following shape:
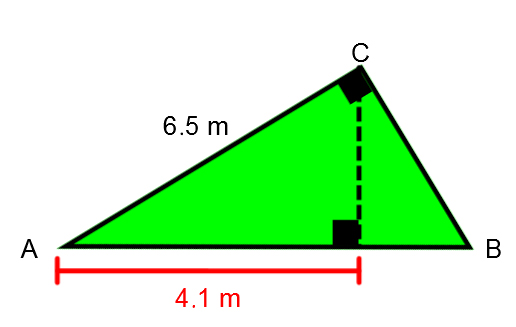
To estimate production costs, the company needs the two missing outer measurements of triangle |(\overline {AB}, \overline {BC}).| Help determine them.
|\text{Distance} = \sqrt{(y_2 - y_1)^2 + (x_2 - x_1)^2}|
where
|(x_1, y_1):| Coordinates of the starting point of the segment
|(x_2, y_2):| Coordinates of the ending point of the segment
To determine the amount of gasoline an airplane needs to complete a Montreal-Paris flight, the cities are represented on a Cartesian plane (graduated in kilometres).
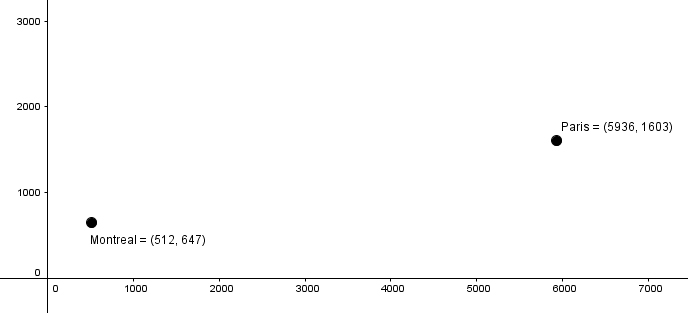
What is the distance between these two cities (in kilometres)?
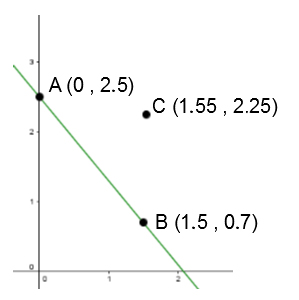
The lines |y_1 = a_1 x + b_1| and |y_2 = a_2 x + b_2| are parallel if and only if |a_1 = a_2.|
What is the equation of the line parallel to that identified in the Cartesian plane below and which passes through point C?
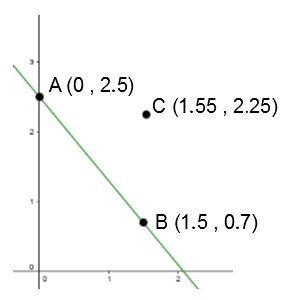
The lines |y_1 = a_1 x + b_1| and |y_2 = a_2 x + b_2| are perpendicular if and only if |a_1 \times a_2 = -1.|
Two lines are also perpendicular if the slope of one is the opposite of the reciprocal of the slope of the other: |a_2 = \dfrac{-1}{a_1}.|
What is the equation of the line perpendicular to that in the Cartesian plane below and which passes through point C?
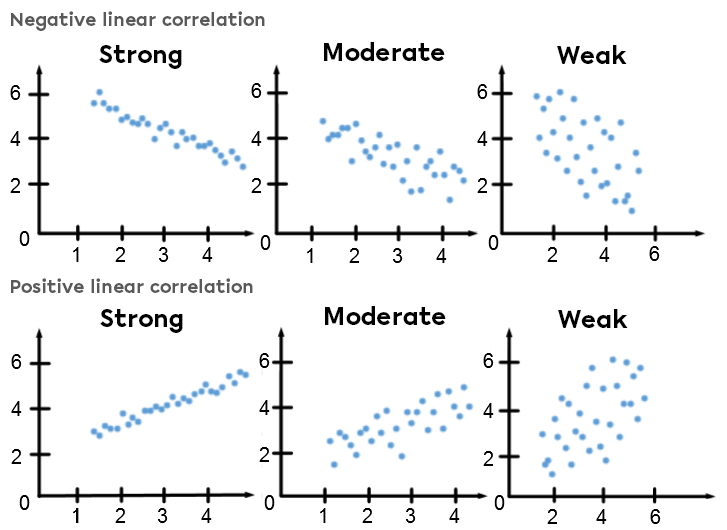
The scatter plot is used to estimate the correlation between two variables. It is necessary to calculate the correlation coefficient to get a more precise idea of the correlation.
A new company has increased its profits for five years and seeks to expand its production centre. However, the owners want to ensure that their company’s economic growth is positive and strong. To break it all down, here's a count of business income for the past 30 weeks.
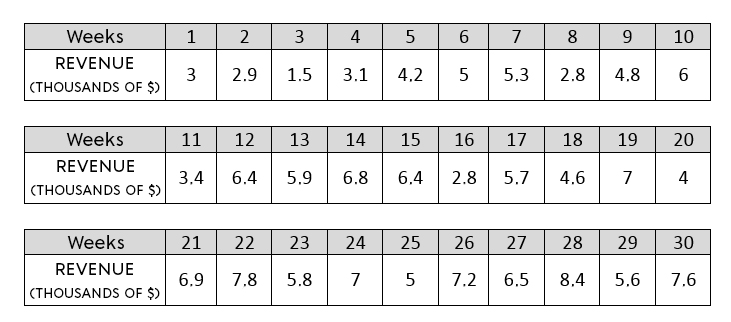
In your opinion, is the economic growth of the company positive and strong?
After framing the scatter plot and taking the length measurement |(l)| and the width |(w)| of the rectangle:
||r = \pm \left(1 - \dfrac{w}{l}\right)||
The sign will depend on the direction of the scatter plot (increasing or decreasing).
This coefficient can also be used to qualify the correlation:
| Value |r| | Linear correlation strength |
|---|---|
| Near |0| | Zero |
| Near |\pm 0{.}50| | Weak |
| Near |\pm 0{.}75| | Average |
| Near |\pm 0{.}87| | Strong |
| Near |\pm 1| | Very strong |
| |\pm 1| | Perfect |
To understand the success of students who enroll in adult education, an administration team is interested in the correlation between absenteeism (in hours) and final grades (in %). They grouped the data into a scatter plot to properly analyze the situation:
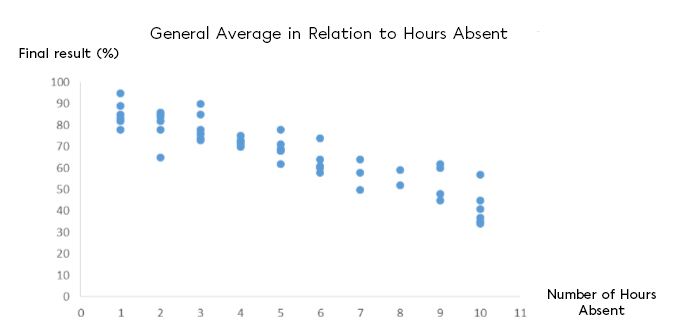
What is the correlation coefficient of this study?
Follow these steps to find the equation of the regression line according to the median-median method:
Arrange the points in ascending order according to the value of |x.|
If possible, divide the pairs into three equal groups.
Calculate the median coordinates |(M_1, M_2, M_3)| of each group.
Calculate the mean coordinates |(P_1)| of the three midpoints.
Calculate the value of the slope |(a)| with |M_1| and |M_3.|
Calculate the value of the initial value |(b)| with |P_1.|
Write the equation of the regression line in the form |y = ax + b.|
Before a new condo tower is built and the landscaping is done, the height of the neighbouring trees is measured so they do not obscure the view for the next 20 years. The following table of values is used to estimate the height of the trees:

Using this information, determine how high the first balconies need to be for the view to remain unobstructed.
Although the situation and data are the same, it is normal that the final answer varies depending on the method used (Median-Median method or Mayer method).
Since these methods are used to estimate and not to predict outcomes with certainty, there may be a difference between the two outcomes.
Follow these steps to find the equation of the regression line according to Mayer’s method:
Arrange the pairs in ascending order according to the value in |x.|
If possible, divide the pairs into two equal groups.
Calculate mean points |(P_1| and |P_2)| of each group.
Use these mean points to find the value of slope |(a)| and the initial value |(b).|
Write the equation of the regression line in the form |y = ax + b.|
Before a new condo tower is built and the landscaping is done, the height of the neighbouring trees are measured so they do not obscure the view for at least 20 years. The following table of values is used to estimate the height of the trees:

Using this information, determine how high the first balconies need to be for the view to remain unobstructed.
Although the situation and data are the same, it is normal that the final answer varies depending on the approach used (Median-Median method or Mayer method).
Since these methods are used to estimate and not to predict outcomes with certainty, there may be a difference between the two outcomes.