Subjects
Grades
Here is a short study guide containing all the concepts covered in secondary 4 in the TS pathway. For further explanation, each formula will be followed by an example and a link to a concept sheet in our virtual library.
Dividing polynomials is done the same way as dividing two numbers using long division.
Find the result of the following division:
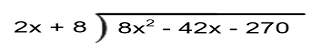
Follow these steps to add or subtract rational expressions:
Find a common denominator.
Calculate equivalent fractions according to the common denominator.
Complete the addition or subtraction of like terms with the numerators.
If possible, simplify the final rational expression by factoring the numerator and denominator
Simplify the following algebraic expression: ||\dfrac{x-2}{x+4} - \dfrac{3}{-3x-12}||
It is important to master the distributive concept associated with multiplication:
If possible, simplify the expressions in brackets.
Distribute each of the terms in the first bracket to all the terms in the second bracket.
Simplify by adding and subtracting like terms.
Find the simplified algebraic expression for the following multiplication: ||(7x + 4) (2x^2 -4x +3)||
Sometimes several factorization methods are required to factor the same algebraic expression, and that is why it is important to master them all.
|
EXAMPLE OF THE PRODUCT-SUM METHOD |
|
|---|---|
|
What measurements (in numerical form or as an algebraic expression) are associated with each of the dimensions of a rectangular prism whose volume is |(4x^2 + 8x - 32 )\ \text{cm}^3|? |
|
|
CALCULATIONS |
EXPLANATIONS |
|
|\begin{align} &4x^2 + 8x - 32 \\ =\ &4 (x^2 + 2x - 8) \end{align}| |
If possible, factor out a greatest common factor, making sure that all coefficients remain whole. |
|
|4 (\color{blue}{x}^2 + \color{red}{2x} \color{green}{-8})| The numbers are |4| and |-2.| |
Determine the numbers that correspond to the product and the sum of the polynomial in brackets. |
|
|\begin{align} &4 (x^2 + \color{red}{2x} - 8) \\ =\ &4 (x^2 + \color{red}{4x -2x} - 8) \\ =\ &4(\left[x^2 + 4x\right] +\left[-2x -8\right]) \\ =\ &4 (\color{blue}{x} (\color{green}{x + 4}) \color{blue}{-2} (\color{green}{x + 4})) \\ =\ &4 (\color{green}{x+4}) (\color{blue}{x-2}) \end{align}| |
Separate the |\color{red}{x}| term into two terms using the two found numbers and then factor using the Grouping method. |
|
The three dimensions measure |4,(x+4),| and |(x-2)\ \text{cm}.| |
|
|
EXAMPLE OF A DIFFERENCE OF SQUARES |
|
|---|---|
|
What are the algebraic expressions that represent the measurement of the base and the height of a triangle whose area is |(2x^2-8)\ \text{m}^2|? |
|
|
CALCULATIONS |
EXPLANATIONS |
|
|\begin{align} \dfrac{\color{blue}{b} \times \color{red}{h}}{2} &= 2x^2 - 8 \\ \color{blue}{b} \times \color{red}{h} &= 4x^2 - 16 \end{align}| |
Create the equation that represents the situation. |
|
|\sqrt{4x^2} = 2x| This is a subtraction between two terms. |
Verify that the binomial meets the criteria of a difference of squares. |
|
|\begin{align} \color{blue}{b} \times \color{red}{h} &= 4x^4 - 16 \\ \color{blue}{b} \times \color{red}{h} &= \color{blue}{(2x - 4)} \color{red}{ (2x + 4)} \end{align}| |
Factor according to this model. |
|
Therefore, we can conclude that |\color{blue}{b=(2x-4)}| and |\color{red}{h=(2x+4)}\ \text{m}.| |
|
|
EXAMPLE OF A PERFECT SQUARE TRINOMIAL |
|
|---|---|
|
What is the algebraic expression associated with the measurement of a square’s edge that has an area of |(\color{blue}{9}x^2 - \color{red}{42}x +\color{green}{49})\ \text{m}^2?| |
|
|
CALCULATIONS |
EXPLANATIONS |
|
|\begin{align} \sqrt{\color{blue}{a}} &= \sqrt{\color{blue}{9}} = \color{blue}{3} \\ \sqrt{\color{green}{c}} &= \sqrt{\color{green}{49}} = \color{green}{7} \\\\ \color{red}{b} &\overset{?}{=} 2 \sqrt{\color{blue}{a}} \sqrt{ \color{green}{c}} \\ \color{red}{42} &= 2 \times \color{blue}{3} \times \color{green}{7}=42\end{align}| |
Verify that the trinomial is indeed a perfect square trinomial. |
|
|\color{blue}{9}x^2 - \color{red}{42}x + \color{green}{49}| |
Factor according to the perfect square trinomial model. |
|
Since the area of a square is calculated using the formula |A=s^2,| we can deduce that |A=(\color{blue}{3x}-\color{green}{7})^2.| By association, we obtain |c=(\color{blue}{3x}-\color{green}{7})\ \text{m}.| |
|
Function form (Standard form)
|y = ax + b| where | a = \dfrac{\Delta y}{\Delta x} = \dfrac{y_2 - y_1}{x_2 - x_1}|
General form
|0 = Ax + By + C| where |A, B, C \in \mathbb{Z}|
With the information provided in the graph below, determine the equation of the line in general form.
|y = a(bx)^2|
where |b=1| unless working with a specific context.
Determine the parabola’s equation with the information provided in the table below.
For second-degree polynomial functions: |a \ne \dfrac{\Delta y}{\Delta x}|
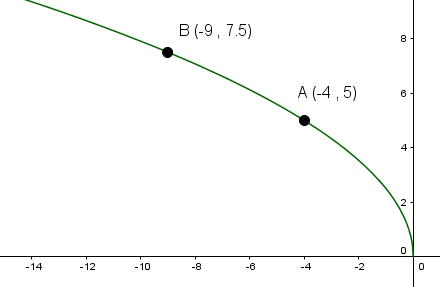
|f(x) = a \sqrt{bx}|
where |b=1| if the function is oriented to the right and |b=-1| if the function is oriented to the left.
Find the equation of the following square root function:
|y = a(c)^{bx}|
where
|a:| Initial value
|c:| Base (multiplying factor)
|b:| Calculation frequency
In 2005, a pond had 500 toads. Its toad population decreases by 5% every three years. If this pace continues, in what year will it have approximately 368 toads?
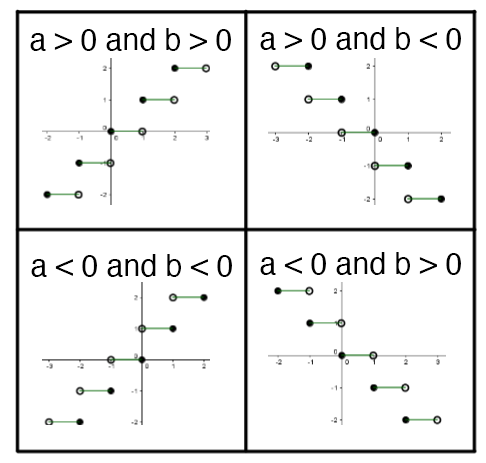
|f(x) = a \left[ b x\right]|
where
|{\mid}a{\mid} = | Vertical distance or height between two steps
|\dfrac{1}{{\mid}b{\mid}} = | Length of a step
To determine the sign of both |a| and |b,| refer to the direction of the open and closed points, and the variation (increasing or decreasing) of the graph:
A grocery store offers a new reward programme with stamps that provide significant discounts on selected items. To determine the number of stamps given to each customer, the grocery store uses the following graph:
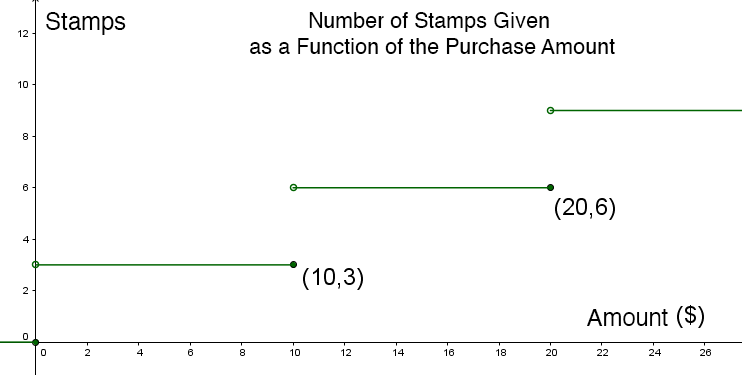
Using this graph, determine the possible purchase amounts if a customer receives |48| stamps.
In a periodic function, a cycle is a repeating pattern, while the period is the length of one cycle along the |x|-axis.
Marie-Claude decides to get back in shape after a vacation by cycling with her group of friends. A coach guides them and decides what speed to maintain. To prepare the group for the next session, the coach gives them the following graph:
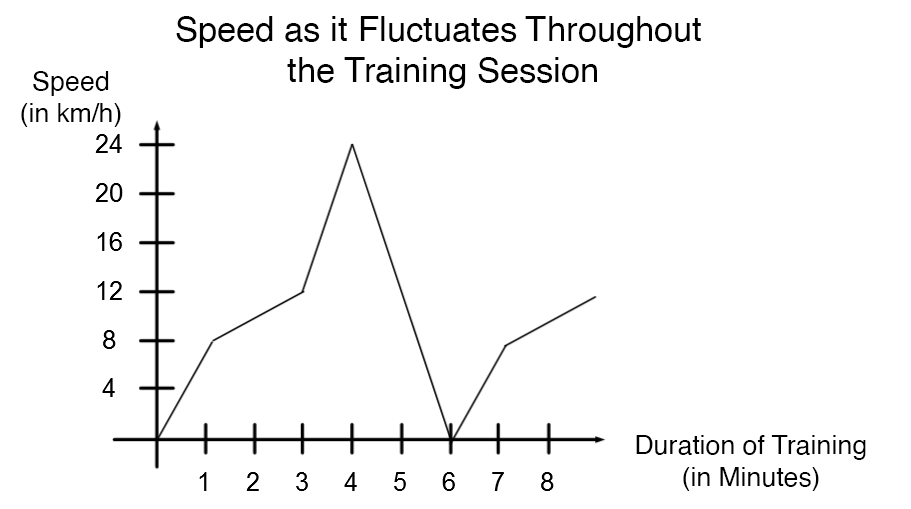
The training consists of repeating the same trip for |45| minutes. How many minutes, in total, will Marie-Claude have pedalled at a minimum speed of |16| km/h?
The inverse of a function |f(x),| denoted |f^{-1}(x),| is obtained by inverting the coordinates of the points such that |(x,y)\rightarrow(y,x).|
Sketch the graph of the inverse of the following function:
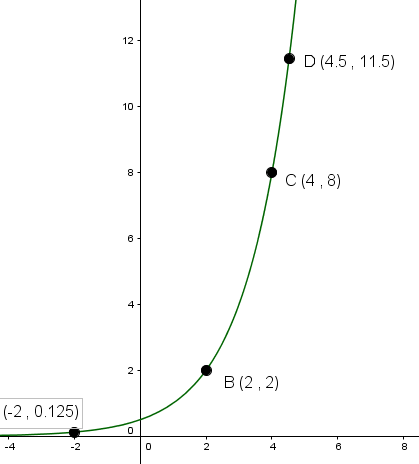
The inverse of a function is not always a function itself. In the cases studied here, these functions are inverses of each other:
Exponential and logarithmic functions
A linear function with respect to itself
A second-degree function (with a restricted domain) and a square root function
The same properties must always be analyzed when studying a function:
Domain: all the possible values of |x|
Range: all the possible values of |y|
X-intercept: the value of |x| when |y=0|
Y-intercept: the value of |y| when |x=0|
Maximum: the greatest value of |y|
Minimum: the smallest value of |y|
Increasing: when the graph goes "upwards" or is constant
Decreasing: when the graph goes "downwards" or is constant
Sign:
Positive sign: the portion of the graph that is above or equal to the |x|-axis
Negative sign: the portion of the graph that is below or equal to the |x|-axis
As an accountant of a large company, you must give a detailed account of the trends in profits over the past year. To help, here is the graph of the last 12 months.
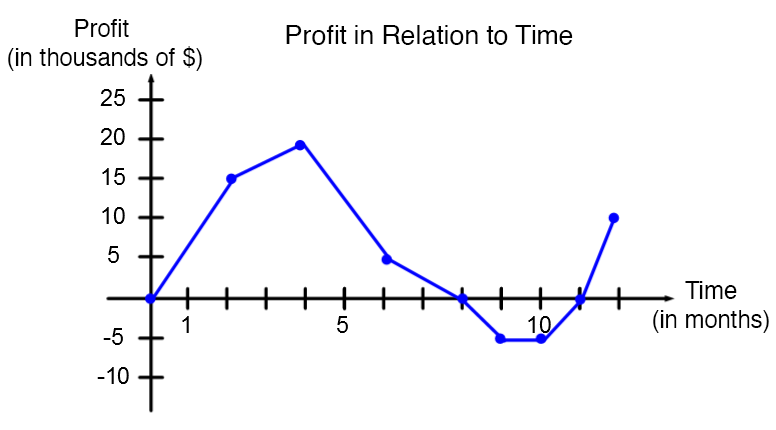
In order to properly support your argument, you must study this graph closely before preparing your presentation speech.
Follow these steps to solve a system of equations using comparison:
Identify the variables associated with the unknowns.
Create the equations according to the scenario.
Isolate the same variable for each of the equations.
Compare the two equations to form a new one.
Solve this new equation.
Substitute the value of the found variable into one of the starting equations to find the value of the other variable.
At a corner store, a group of workers buys 4 coffees and 6 muffins for |$15.06.| The next day, they buy |3| coffees and |5| muffins for a total of |$11.97.| If the following day they want to buy |6| coffees and |4| muffins, how much will it cost?
Follow these steps to solve a system of equations using substitution:
Identify the variables associated with the unknowns.
Create the equations according to the scenario.
Isolate a variable in one of the two equations.
Substitute this same variable in the other equation by the algebraic expression associated with it.
Solve this new equation.
Substitute the value of the found variable into one of the starting equations to find the value of the other variable.
At a corner store, a group of workers buys |4| coffees and |6| muffins for |$15.06.| The next day, they buy |3| coffees and |5| muffins for a total of |$11.97.| If the following day they buy |6| coffees and |4| muffins, how much will it cost?
Follow these steps to solve an equation system using the elimination method:
Identify the variables associated with the unknowns.
Create the equations according to the scenario.
Find equivalent equations to obtain the same coefficient for the same variable.
Subtract the two equations.
Isolate the remaining variable to find its value.
Substitute the value of the found variable in one of the starting equations to find the value of the other variable.
At a corner store, a group of workers buys 4 coffees and 6 muffins for |$15{.}06.| The next day, they buy 3 coffees and 5 muffins for a total of |$11{.}97.| If the following day they buy 6 coffees and 4 muffins, how much will it cost?
In general, the law of multiplying radicals is used to carry out the factorization |(\sqrt{ab}=\sqrt{a}\sqrt{b}).| To do so:
Decompose the radicand into a product of factors, where one factor is a square number.
Transform the root of a product into a product of roots |(\sqrt{ab}=\sqrt{a}\sqrt{b}).|
Calculate the root of the square number.
What is the simplified value of the following radical: ||\sqrt{45}||
We can deduce three theorems from the following right triangle.
In a right triangle, the measurement of each side of the right angle is the geometric mean between its projection onto the hypotenuse and the hypotenuse itself.||\begin{align} \dfrac{m}{a} = \dfrac{a}{c}\ &\Leftrightarrow\ a^2 = m c \\\\ \dfrac{n}{b} = \dfrac{b}{c}\ &\Leftrightarrow\ b^2 = n c \end{align}||
In a right triangle, the height measurement (altitude) is the geometric mean of the projections of the sides onto the hypotenuse. ||\dfrac{m}{h} = \dfrac{h}{n}\ \Leftrightarrow\ h^2 = m n||
In a right triangle, the product of the measures of the hypotenuse and the height (altitude) equals the product of the measurements of the sides of the right angle. ||c h = a b||
To stand out from other contractors, a construction company suggests houses with roofs of different shapes. Among these choices, we have the following form:
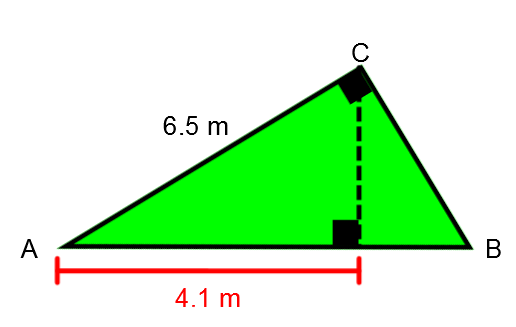
The company manager needs the two missing outer measurements of triangle |(\overline{AB},\overline{BC})| to estimate the production costs. Help him find them.
Considering the angle |\theta| as a reference, we have:
|\sin \theta = \dfrac{\text{Measurement of side opposite to}\ \theta}{\text{Measurement of the hypotenuse}}|
|\cos \theta = \dfrac{\text{Measurement of the side adjacent to}\ \theta}{\text{Measurement of the hypotenuse}}|
|\tan \theta = \dfrac{\text{Measurement of the side opposite to} \ \theta}{\text{Measurement of side adjacent to} \ \theta}|
The elevation angle of a house's roof trusses must be a minimum of |25^\circ| for building standards to be met. To ensure that this constraint is respected, a manufacturer decides to establish this angle at |35^\circ.| If the length of the roof truss is |13| metres, what will be the measurements of the other two sides?
To determine the route a helicopter should take to pick up people in the woods who need help, a map of the region has been triangulated with the helicopter’s current location, the hospital and the people who are in distress.
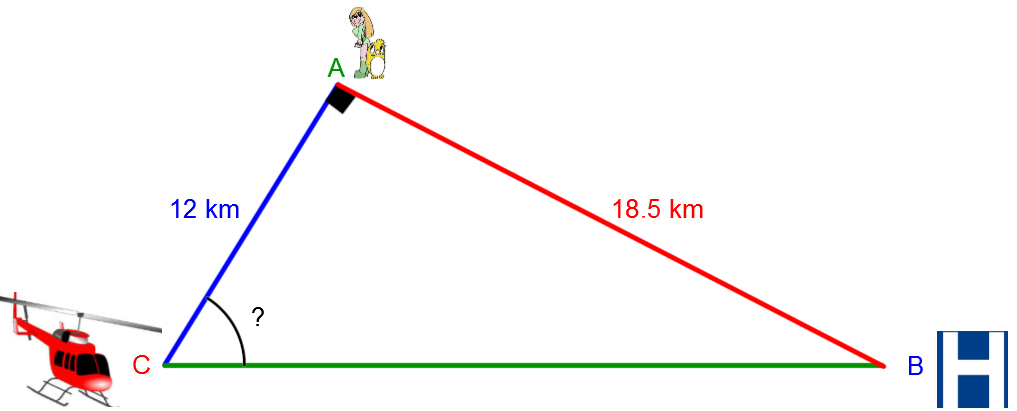
According to this drawing, what angle of orientation should the helicopter take to reach the people as quickly as possible?
To find this, you have to add lines (usually a height) with particular properties and unknown measures.
Choose the correct vertex from which to draw a height.
Use the trigonometric ratios in the right triangle to find the missing measurements.
Apply the formula for the area of a triangle with the found measurements.
Find the area of the following triangle:
A - S - A: Two triangles are congruent (isometric) when a pair of corresponding congruent sides is located between two pairs of corresponding congruent angles.
S - A - S: Two triangles are congruent (isometric) when a pair of corresponding congruent angles is located between two pairs of corresponding congruent sides.
S - S - S: Two triangles are congruent (isometric) when all of the pairs of corresponding sides are congruent.
Due to machinery problems at a construction company, employees have to assemble the triangular-shaped roof trusses themselves to complete the construction on a house. All of the roof trusses must be identical.
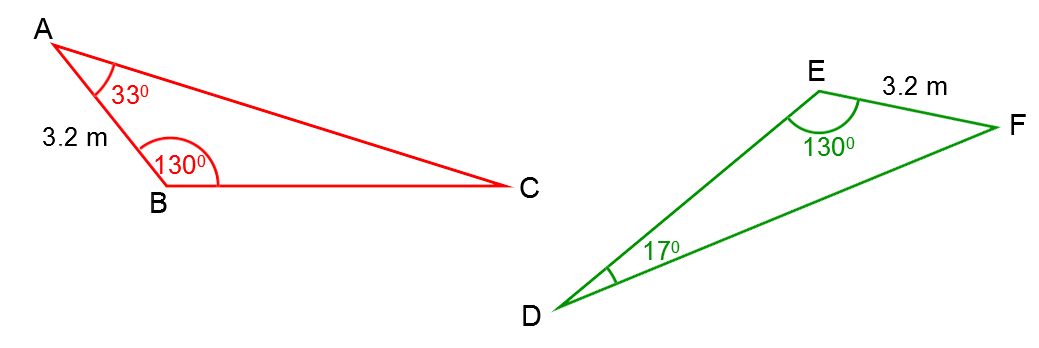
Using the information provided above, demonstrate that these two constructions are congruent (isometric).
A - A: Two triangles are similar when two pairs of corresponding angles are congruent.
S - A - S: Two triangles are similar when a pair of congruent corresponding angles is located between two pairs of proportional corresponding sides.
S - S - S: Two triangles are similar if all three pairs of corresponding sides are proportional.
The city is organizing a family run for a community fundraiser. They want the path taken by adults to be similar to that taken by the children.
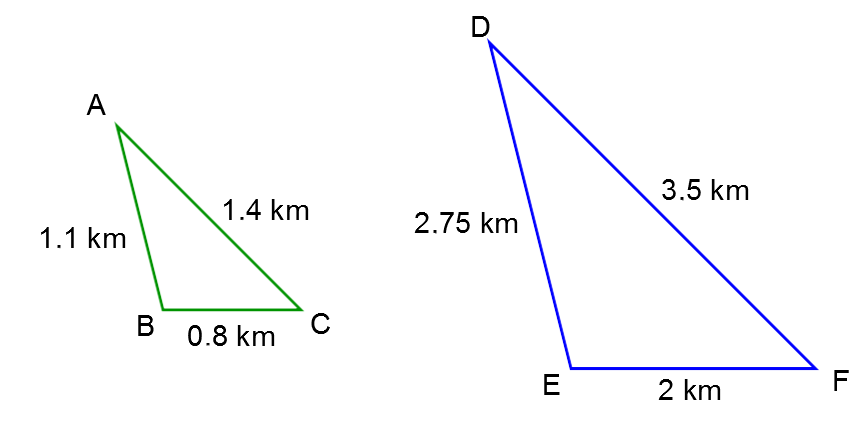
Considering the information given above, demonstrate that the two paths are similar.
|\text{Distance} = \sqrt{(y_2 - y_1)^2 + (x_2 - x_1)^2}|
where
|(x_1, y_1):| Coordinates of the starting point of the segment
|(x_2, y_2):| Coordinates of the ending point of the segment
To determine how much gasoline an airplane must have to complete a Montreal-Paris flight, both cities are represented on a Cartesian plane graduated in kilometres.
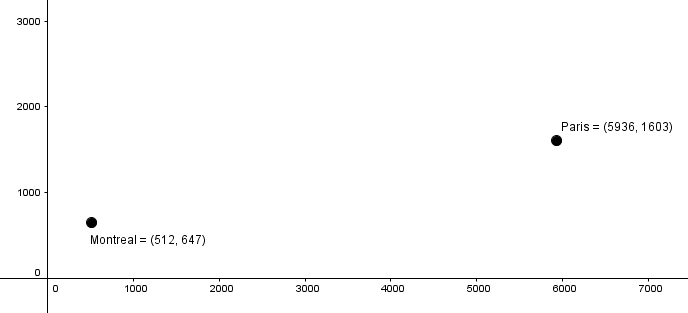
What is the distance in kilometres between these two cities?
Consider |(x,y),| the coordinates of the desired division point. ||x=x_1+ \dfrac{a}{b} (x_2-x_1)|| ||y=y_1+ \dfrac{a}{b} (y_2-y_1)||
where
|(x_1,y_1):| Starting point of the segment
|(x_2,y_2):| Endpoint of the segment
|\dfrac{a}{b}:| Fraction that defines the division of the segment (part to whole)
Every morning, you wait at the bus stop for the bus to take you to school. You noticed that for the stop to be on-route for the other students in the area, it divides the segment of the street from your house to the school into a ratio of |1:4.|
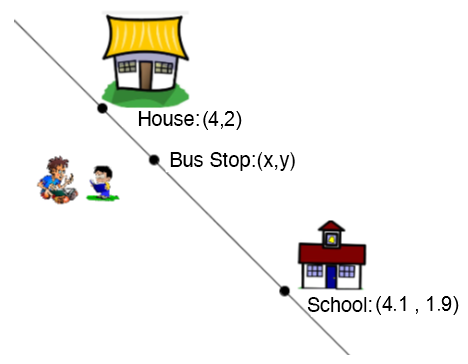
Using the information provided, determine the coordinates of your bus stop’s location.
It is important to differentiate between the two types of notations used to illustrate the portion associated with a division point. This is done in order to then use the appropriate notation for the formula: ||\begin{matrix}\text{Ratio}\\ a:b\end{matrix}\Leftrightarrow\begin{matrix}\text{Fraction}\\ \dfrac{a}{a+b}\end{matrix}||
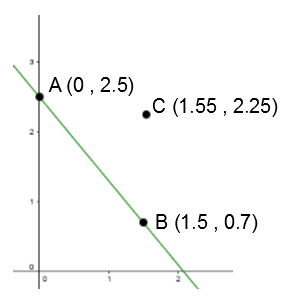
The lines |y_1=a_1x+b_1| and |y_2=a_2x+b_2| are parallel if and only if |a_1=a_2.|
What is the equation of the line that is parallel to the one identified in the Cartesian plane below and passes through point C?
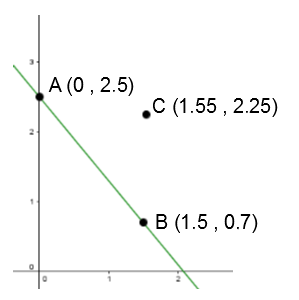
The lines |y_1=a_1x+b_1| and |y_2=a_2x+b_2| are perpendicular if and only if |a_1\times a_2=-1.|
In other words, two lines are perpendicular if the slope of one is the opposite of the reciprocal of the slope of the other: |a_2=\dfrac{-1}{a_1}.|
What is the equation of the line that is perpendicular to the one identified in the Cartesian plane below and passes through point |C|?
|
TYPES OF EVENTS |
DEFINITION |
EXAMPLE |
|---|---|---|
|
Mutually Exclusive |
When the events can't happen at the same time. |
Roll a six-sided die and get a result that is a multiple of both 3 and 4. |
|
Not Mutually Exclusive |
When the events can occur at the same time. |
Draw a random card from a deck of 52 cards and get one that is both red and an ace. |
|
Dependent |
When the occurrence of one affects the occurrence of the other. |
Draw two cards successively, without replacement, from a deck that contains 52 cards at the start. |
|
Independent |
When the occurrence of one does not affect the occurrence of the other. |
Choose a card from a deck that contains 52 cards and roll a six-sided die. |
Do not forget the types of events that have been seen in previous years (certain, probable, impossible, elementary, complementary, compatible, and incompatible).
Consider |a,| the odds for and |b,| the odds against. Therefore:
A ratio of odds for |= a : b \Rightarrow \dfrac {a}{a+b}|
RA ratio of odds against |= b : a \Rightarrow \dfrac {b}{b+a}|
Thus, the net gain is obtained according to the following proportion: ||\dfrac{\text{Bet Amount}}{\text{Net Gain}}=\dfrac{\text{No. of chances bet on}}{\text{No. of total chances}}||
During the days of the Quebec racetrack, it was possible to bet on the victories of racehorses. Each horse had a rating which quantified its chances of winning. For the last race, a fan bet |$20| on the victory of a horse whose odds for winning were |1:14.| What was the potential payout (net gain) of his bet?
For some boxing matches, the outcome of a match can be bet upon. Each fighter has a rating which quantifies their chances of winning. The champion has |44:1| chances of winning the next fight. If a fan bet |$10| against the champion's victory, what would be their net gain?
|\mathbb{E} = (p_1 x_1 + p_2 x_2 + \dots + p_i x_i) - M|
where
|p_i =| Probability of occurrence of the event |i|
|x_i =| Amount associated with the event |i|
|M =| Initial bet amount
If |\mathbb{E}=0,| then the game is fair.
If |\mathbb{E}<0,| then the game is unfavourable to the player.
If |\mathbb{E}>0,| then the game is favourable to the player.
To finance the school's freestyle ski team, organizers set up a fundraising activity for which it is possible to win the following prizes:
A weekend family ski pass (value of |$800|)
Two alpine ski season tickets (value of |$500| each)
Four pairs of skis (value of |$300| each)
Eight lift tickets, valid for one day (value of |$45| each)
There are |336| tickets to sell. What should the selling price of a ticket be to ensure the raffle is fair?
|P(A \mid B) = \dfrac{P (A \cap B)}{P (B)}|
where |P(A) >0|
During the previous month, listeners of a Quebec radio channel had the chance to win a trip to Walt Disney World. Before randomly drawing for the winner, the broadcaster provided an overview of the participants:
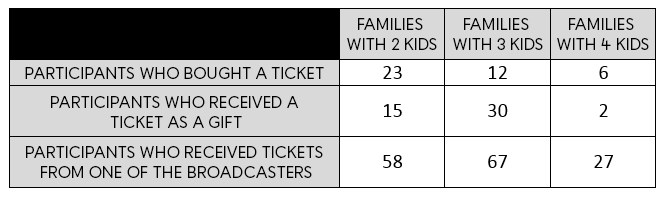
With the knowledge that he was given the raffle ticket as a gift, what is the probability that the winner will be the father of a family of three children?
|EM = \dfrac{\sum \mid x_i - \overline {x} \mid}{n}|
where
|x_i| each data point
|\sum| the sum
|n| the total number of data
Over the last month, 11 houses in the same neighbourhood were sold for the following prices:
|\color{blue}{$\ 156\ 700},\color{red}{$\ 158\ 900},$\ 159\ 000,$\ 162\ 500,$\ 164\ 100,$\ 167\ 400,$\ 172\ 000,$\ 175\ 000,$\ 178\ 100,$\ 179\ 000,$\ 183\ 000.|
For statistical purposes, calculate the mean deviation of this distribution.
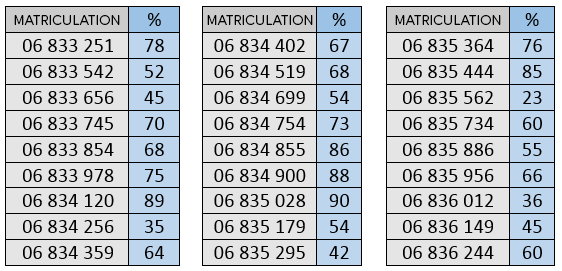
For a sample: |s= \sqrt{\dfrac{\sum(x_{i}-\overline{x})^{2}}{n-1}}|
For a population: |\sigma = \sqrt{\dfrac{\sum(x_i-\mu)^2}{N}}|
where
|\sum| a sum of several elements.
|x_i| the |i^\text{th}| distribution value.
|\overline{x}| the sample mean and |\mu,| the average of the population.
|n| the sample size and |N,| the size of the population.
In some university courses, professors assign marks based on exam scores and the standard deviation of the distribution. What is the standard deviation of the following distribution?
The scatter plot is used to estimate the correlation that exists between two variables. To get a more precise idea of the correlation, you must calculate the correlation coefficient.
A new company has increased its profits in the last five years and wishes to expand its production centre. However, the owners want to ensure that the economic growth of their company is positive and strongly correlated. To break it all down, here's a count of business income for the past 30 weeks.
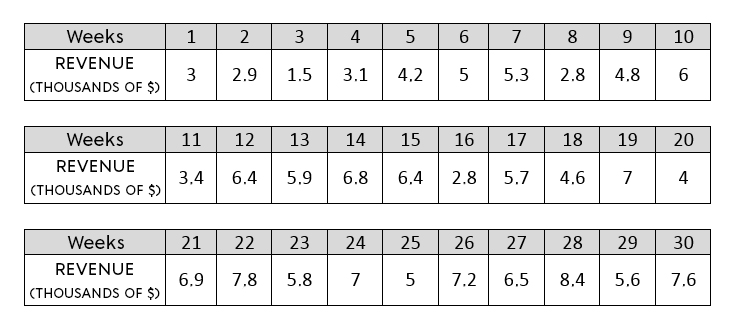
In your opinion, is the economic growth of the company positive and strongly correlated?
After framing the scatter plot and measuring the length |(L)| and width |(l)| of the rectangle, we have:||r = \pm \left(1 - \dfrac{l}{L}\right)||As for the sign, it depends on the direction of the scatter plots (increasing or decreasing).
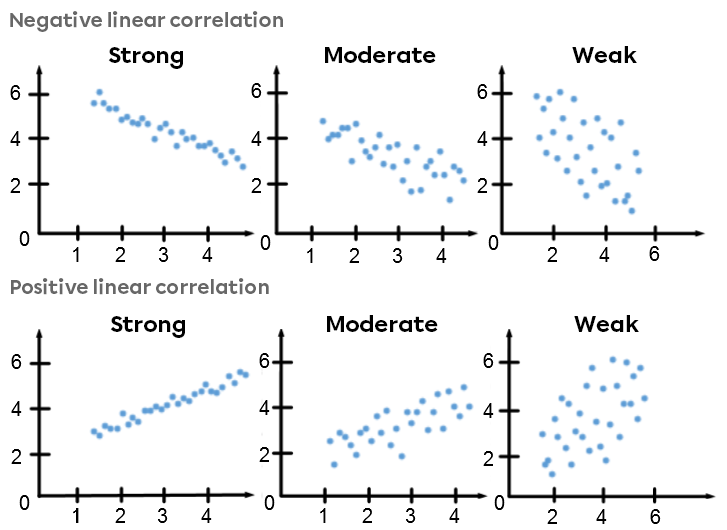
This coefficient can also be used to qualify the correlation:
|
Value |r| |
Linear correlation strength |
|---|---|
|
Near |0| |
Zero |
|
Near |\pm0.50| |
Weak |
|
Near |\pm0.75| |
Moderate |
|
Near |\pm0.87| |
Strong |
|
Near |\pm1| |
Very strong |
|
|\pm 1| |
Perfect |
To take stock of the success of students who enroll in adult education, the administration team is interested in the correlation between absenteeism (in hours) and the students’ final grades (in %). To analyze everything properly, they grouped the data into a scatter plot:
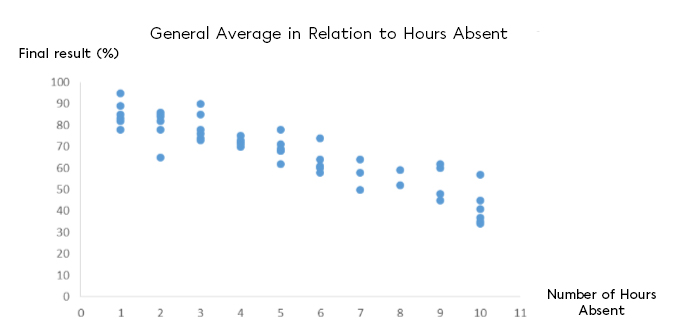
What is the correlation coefficient of this study?
Follow these steps to find the equation of the regression line according to the median-median method:
Rearrange in ascending order according to the value of |x.|
If possible, divide the points into three equal groups.
Calculate the median coordinate |(M_1,M_2,M_3)| of each group.
Calculate the mean coordinates of point |(P_1)| of the three midpoints.
Calculate the value of slope |(a)| with |M_1| and |M_3.|
Calculate the value of the initial value |(b)| with |P_1.|
Write the equation of the regression line in the form |y=ax+b.|
Before a new condo tower is built and the landscaping is done, the heights of the surrounding trees are measured to ensure they do not obscure the view for at least 20 years. The following table of values is used to estimate the height of the view:

Using this information, determine how high the first balconies should be for the view to remain unobstructed by trees.
Although the situation and data are the same, it is normal that the final answer varies depending on the method used (Median-Median method or Mayer method).
Since these methods are used to estimate rather than to predict outcomes with certainty, there may be a difference between the two outcomes.
To find the equation of the regression line according to Mayer's method, follow these steps:
Rearrange the points in ascending order according to the value of |x.|
If possible, divide the points into two equal groups.
Calculate the mean points |(P_1\text{ and }P_2)| of each group.
Use these mean points to find the value of slope |(a)| and the initial value |(b).|
Write the equation of the regression line in the form |y=ax+b.|
Before a new condo tower is built and the landscaping is done, the height of the surrounding trees are measured to ensure they do not obscure the view for at least 20 years. The following table of values is used to estimate the height of the view:
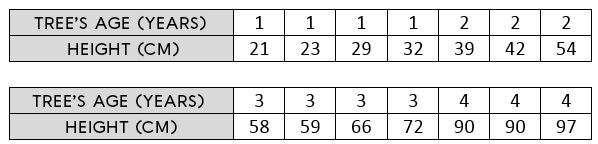
Using this information, determine how high the first balconies should be for the view to remain unobstructed by trees.
Although the situation and data are the same, it is normal that the final answer varies depending on the method used (Median-Median method or Mayer method).
Since these methods are used to estimate rather than to predict outcomes with certainty, there may be a difference between the two outcomes.