Subjects
Grades
The Area of a Cube
Concept sheet | Mathematics
Secondary
2
Table of contents
Area of a Base
Given the particular properties of a cube, several pairs of congruent sides can form its bases. The bases of a cube are always two congruent squares. Thus, we can use the following formula.
||A_\text{b} = s^2|| where ||\begin{align}A_b&= \text{Area of a base}\\s &= \text{side}\end{align}||
Note: if the area of the bases is needed, you must multiply the area of one base by |2| since there are two congruent bases.
Calculate the area of the bases of the following cube.
-
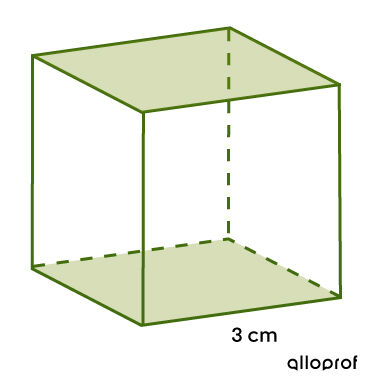
Identify the relevant faces
In this case, they are already identified. -
Apply the formula
It is a cube, so the following formula can be applied. ||\begin{align}A_\text{b} &= \color{#3a9438}{s}^2 \\ &= \color{#3a9438}{3}^2\\ &= 9\ \text{cm}^2\end{align}||Since we are looking for the area of the bases, multiply the area of one base by 2. ||\begin{align}A_\text{bases} &= 2\times 9 \\ &= 18\ \text{cm}^2\end{align}|| -
Interpret the answer
Therefore, the cube’s bases have a total area of |18 \ \text{cm}^2.|
Due to the particular construction of a cube, the same reasoning can be applied for the lateral area.
Lateral Area
Since the four lateral faces are congruent squares, simply calculate the area of one face and multiply it by |4| to obtain the lateral area.
||A_L = 4 s^2|| where ||\begin{align} A_L &= \text{Lateral area of a cube}\\s &= \text{side}\end{align}||
We want to paint the four walls of a cube-shaped room the same colour. Knowing that one can of paint covers |32\ \text{m}^2,| determine the number of cans needed to complete the job.
-
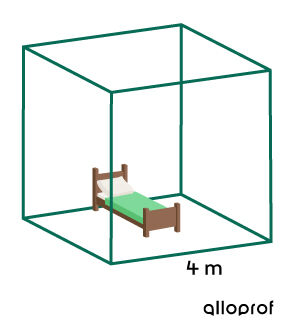
Identify the relevant faces
There are four walls which form the lateral area and need to be painted.
-
Apply the formula
||\begin{align}A_L &= 4 c^2 \\ &= 4 (4)^2 \\ &= 64 \ \text{m}^2\end{align}|| -
Interpret the answer
Since it is necessary to cover an area of |64 \ \text{m}^2| and one can of paint covers |32 \ \text{m}^2,| simply divide as follows. ||64\ \text{m}^2 \div \dfrac{32\ \text{m}^2}{1\ \text{can}} = 2\ \text{cans}|| To paint the four walls, |2| cans of paint will be needed.
Total Surface Area
Once again, use the fact that a cube’s faces are composed of six congruent squares to derive its area formula.
||A_T = 6 s^2|| where ||\begin{align}A_T&= \text{Total area of a cube}\\s &= \text{side}\end{align}||
In fact, it is simply a matter of calculating the area of one of the faces and multiplying it by |6| since they are congruent.
Note: since a cube is also a prism, the following formula can equally be used: |A_T=2A_b+A_L.|
A company is tasked with polishing and restoring the lustre of dice used in their casinos. If polishing costs |$0{.}25\ / \text{cm}^2,| how much will it cost to polish 200 dice?
-
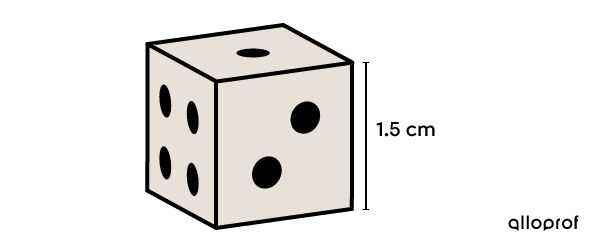
Identify the relevant faces
In this case, the six faces must be polished. -
Apply the formula
||\begin{align} A_T &= 6 c^2 \\ &= 6 (1{.}5)^2 \\ &= 13{.}5 \ \text{cm}^2\end{align}|| -
Interpret the answer
If there are |200| dice, the total surface area is ||\dfrac {13{.}5\ \text{cm}^2}{1\ \text{die}} \times 200\ \text{dice} = 2\ 700\ \text{cm}^2|| Since it costs |$0{.}25\ / \text{cm}^2| : ||2\ 700\ \text{cm}^2 \times $0{.}25\ / \text{cm}^2 = $675\ || It will cost |$675\ | to polish all the dice of the casinos.
In some cases, a missing side measurement may be sought from a given area. This is called finding a missing measurement of a cube from its area. In this context, the approach is a little different, but it is still essential to remember the formula for finding the surface area of a cube.