The Area of Prisms

To attract potential customers, a company prints a life-size image of a boxed toy on the base of its packaging. Based on the measurements of the box shown below, determine the area covered by the printed image.

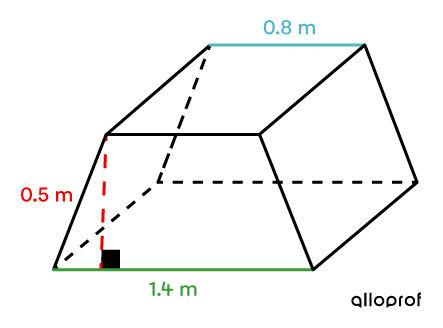
1. Identify the relevant surfaces
   The bases are two trapezoids since they are the only two figures in this solid that are both parallel and congruent.

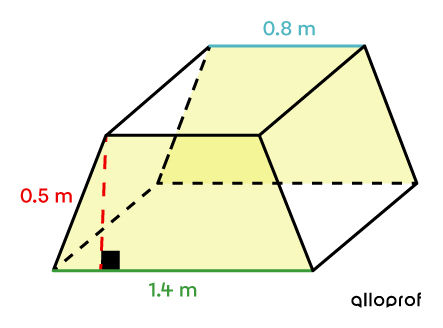
2. Apply the appropriate formula
   Calculate the area of a trapezoid using the following formula: ||\begin{align} A_\text{b} &= A_\text{trapezoid} \\&=\dfrac{(\color{#3A9A38}{B} + \color{#51B6C2}{b}) \times \color{#EC0000}{h}}{2}\\&= \dfrac{(\color{#3A9A38}{1{.}4} + \color{#51B6C2}{0{.}8}) \times \color{#EC0000}{0{.}5}}{2}\\&= 0{.}55 \ \text{m}^2\end{align}||

3. Interpret the answer
   Since there are 2 bases, multiply the previous result by 2: ||\begin{align} A_\text{bases} &= 0{.}55 \times 2\\&= 1{.}1 \ \text{m}^2\end{align}||
   Answer: The surface area covered by the printed images (the 2 bases) is |1{.}1\ \text{m}^2.|

||A_L = P_b \times h|| where ||\begin{align} A_L&=\text{Lateral area} \\ P_b &= \text{Perimeter of a base}\\ h\ &= \text{Prism height}\end{align}||

A candy company wants to sell a new chocolate bar in the following shape:

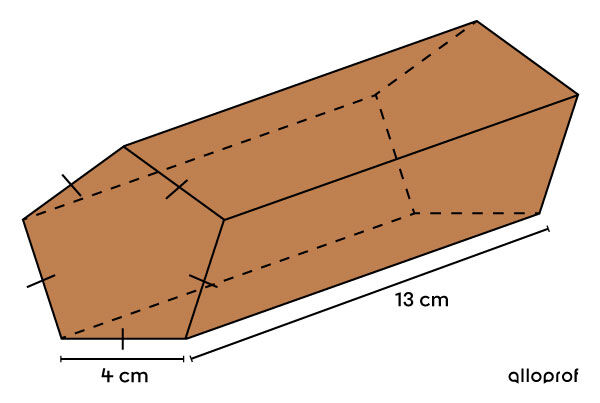
In addition, the packaging on the lateral faces requires more expensive paper. To limit the costs, determine the measurement of the lateral area.

1. Identify the solid
   It is a regular pentagonal-based prism.

2. Apply the formula for the lateral area of the identified solid
   ||\begin{align}A_L &= P_b \times h\\ &= (4 + 4 + 4 + 4 + 4) \times 13\\ &= 260 \ \text{cm}^2\end{align}||

3. Interpret the answer
   The measurement of the lateral area of the chocolate bar is |260 \ \text{cm}^2.|

The formula is based on the net of the solid.

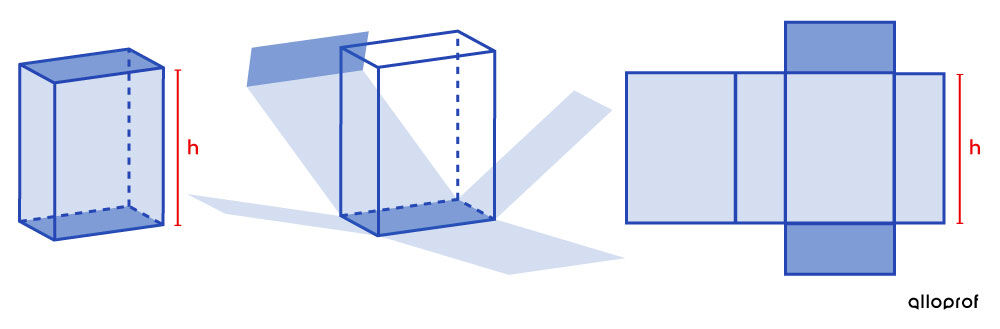
The lateral area can be drawn with a single large rectangle.

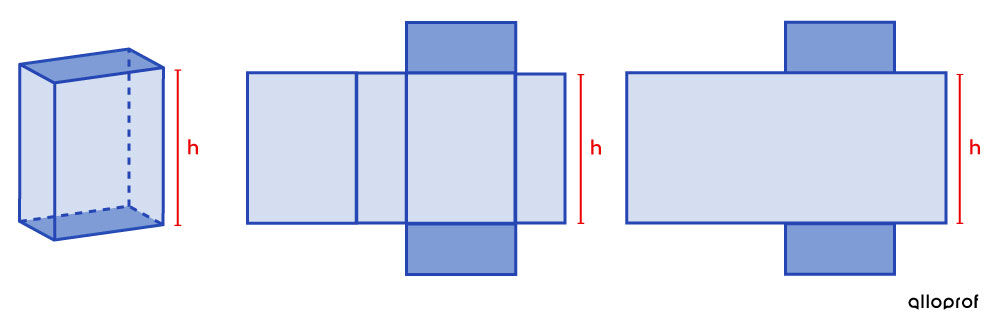
Measuring the length of the rectangle’s base is equivalent to measuring the perimeter of the prism’s base.

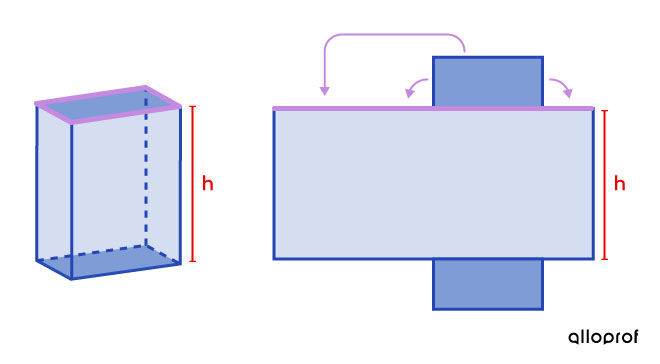
This is the reason why the perimeter of the base is included in the formula for calculating the lateral area of a prism.

||A_T = 2 A_b + A_L|| where ||A_T=\text{Total area}||

A tent needs to be coated with an aerosol product to ensure it is waterproof. However, a can of this product only covers an average area of |6 \ \text{m}^2.|

Based on the measurements in the following drawing, determine how many cans are needed to completely waterproof the tent.

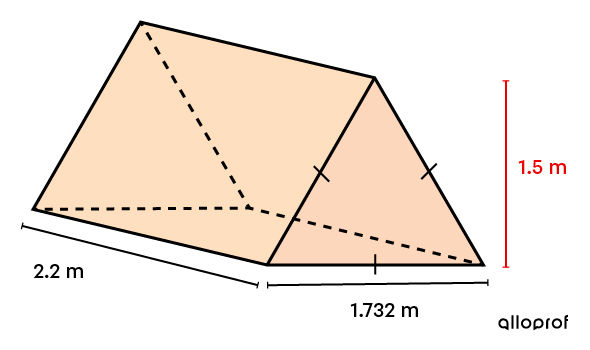
1. Identify the relevant faces
   The tent must be waterproofed completely. Thus, the area of the 5 faces must be calculated.

2. Calculate the area of a base
   Since this is a triangular prism, apply the formula for the area of a triangle. ||\begin{align} A_\text{b} &= A_\text{triangle}\\ &= \frac{b \times \color{#EC0000}{h}}{2}\\ &= \frac{1{.}732 \times \color{#EC0000}{1{.}5}}{2}\\ &= 1{.}299 \ \text{m}^2\end{align}||

3. Calculate the lateral area
   Since it is a prism, apply the following formula. ||\begin{align} A_L &= P_b \times h\\ &= (1{.}732 + 1{.}732 + 1{.}732) \times 2{.}2\\ &\approx 11{.}431 \ \text{m}^2\end{align}||

4. Calculate the total area
   ||\begin{align} A_T &= 2 A_b + A_L \\ &= 2 \times 1{.}299 + 11{.}431 \\ &= 14{.}029 \ \text{m}^2\end{align}||

5. Interpret the answer
   To determine the total number of cans to buy, we must divide |14{.}029\ \text{m}^2 \div 6\ \text{m}^2/\text{can} \approx 2{.}34\ \text{cans}.|

Answer: Since only full cans can be purchased, a total of |3| full cans are needed.