Subjects
Grades
In some problems, the solid’s area and all of its measurements, except one, are given. In these cases, it is necessary to know how to find this missing measurement.
The procedure for finding a solid’s missing measurement is generally the same regardless of the type of solid. The following are the main steps.
Identify the measurements given.
Determine the formula to use.
Replace the variables with the given measurements.
Isolate the sought variable.
A toy company wants to replace some of the sides of their cardboard boxes with a thick transparent material to enable customers to see the packaged products inside. To order the material, the company needs to know the box’s dimensions. Given that the total area of the box is |2\ 646\ \text{cm}^2,| determine the measure of the box’s edges.

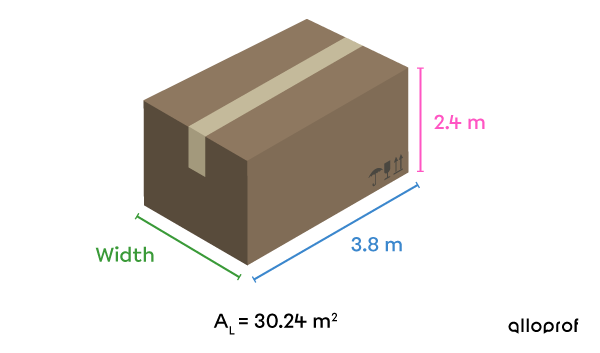
Before making a delivery, a trucker must ensure that the dimensions of the object being transported does not exceed the width of the trailer. He only has access to the measurements identified in the following image for his next delivery. Help him determine the measure of the box’s width.

Moments in the video:
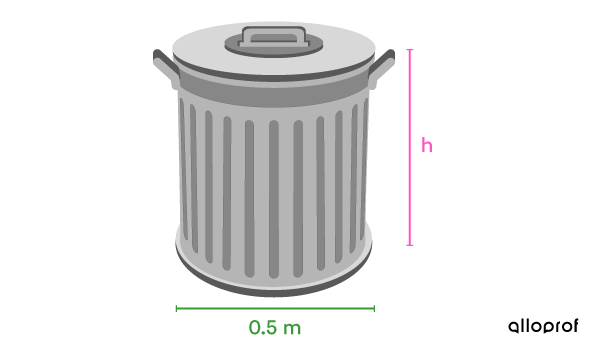
Sergei wants to coat his new lidded, cylindrical trash can with an anti-rust coating. His neighbour tells him about a product that covered his |1{.}335\ \text{m}^2| garbage can with a single coat. However, Sergei's trash can is twice as tall as his neighbour's. If the diameter of his neighbour’s garbage is |0{.}5\ \text{m}|, how tall is Sergei's trash can?
What is the measure of a tennis ball’s radius if a cylindrical container that can hold exactly 3 balls has a lateral area of |379{.}84\ \text{cm}^2|?

Moments in the video:
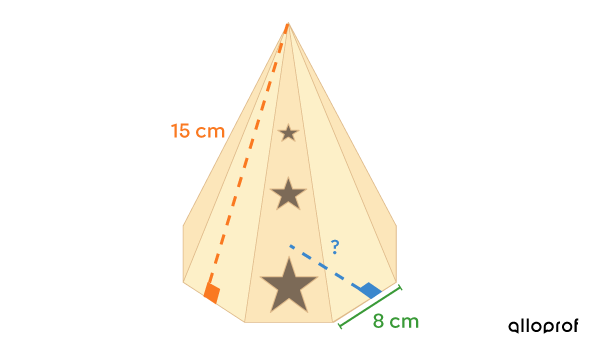
Gabriela wants to buy a decorative incense burner for her living room. The burner is a regular octagonal pyramid. Gabriela doesn't know if it can fit on a shelf |15\ \text{cm}| deep.
Gabriela knows the total area of the incense burner is |789{.}12\ \text{cm}^2.| The apothem of the pyramid is |15\ \text{cm}| and the measure of one side of the octagon is |8\ \text{cm}.|
Can the incense burner fit on the shelf if the base’s apothem |(\color{#3B87CD}{a_b})| is perpendicular to the wall?
Since a regular pyramid is, in fact, a pyramid with a regular polygon as its base, be careful not to confuse the base’s apothem with that of the pyramid.
The apothem is usually identified by the variable |a.| To differentiate between the two apothems, add a subscript. Thus, the pyramid’s apothem becomes |a_p| and the base’s apothem becomes |a_b.| The choice of the subscript or the way of identifying the 2 measures may vary in different contexts.
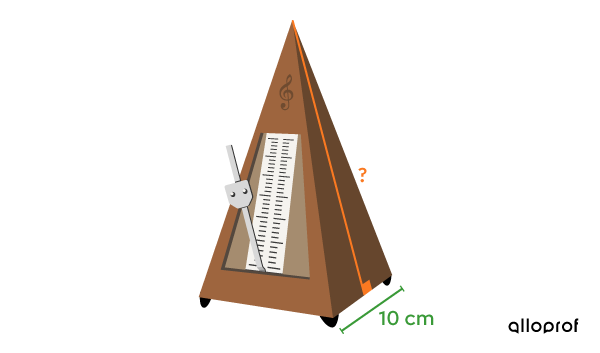
Stefan plays piano and he frequently uses an old metronome that is shaped like a square-based pyramid.
To polish the metronome, he needs to know the measure of the pyramid’s apothem. He knows that the base of the metronome measures |10\ \text{cm}| and the total area of the pyramid is |512{.}4\ \text{cm}^2.|
What is the measure of the metronome’s apothem?

Moments in the video:
Parents bought cone-shaped party hats to distribute to all the guests at their child’s birthday party. To ensure that the model found online is large enough for the children's heads, they need to know the measure of the circle’s radius at the base of the hat.
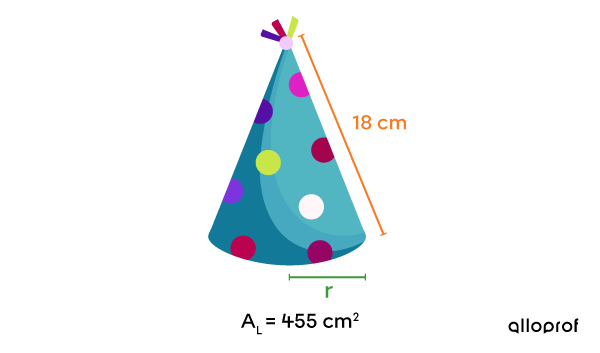
Since pyramids and cones have a similar shape, the procedure for finding the measurement of the cone’s apothem is the same as that of a pyramid.
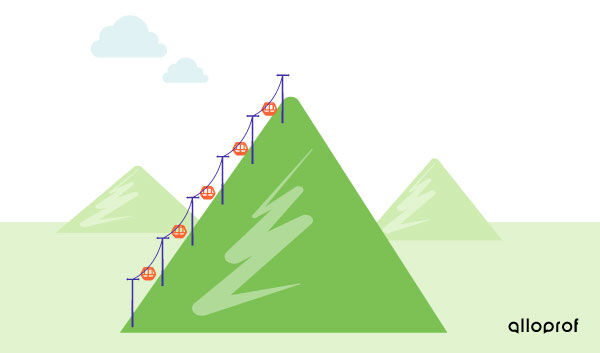
A resort wants to install a ski lift to provide a panoramic view. To complete this project, the resort needs to know the distance between the foot of the mountain and the summit.
Using topographic maps of the region, the lateral area of the conical-shaped mountain is estimated to be |1{.}7\ \text{km}^2| and the measurement of the radius of the base is about |500\ \text{m}.| What should be the ski lift’s length, to the nearest metre?
Sometimes, the height of a pyramid or cone must be determined from the area even though it is not in the formula for the area. In that case, find the apothem of the solid or the radius of the base. Then, use the Pythagorean Theorem to calculate the height.
Whether for a pyramid or a cone, the procedure is very similar.
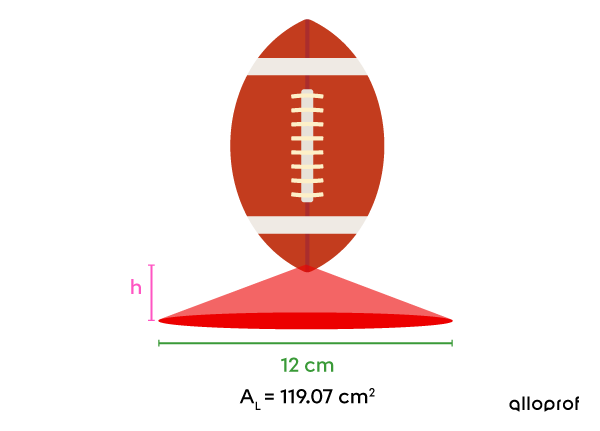
During kickoffs in football games, kickers often use small cone-shaped stands to hold the ball upright.
If the tip of the ball coincides with the apex of the cone, how far is the ball from the ground when it is on the stand?
The previous example demonstrates that it is usually necessary to find the measure of the apothem before determining the height using the Pythagorean Theorem. Finding the height of a cone or pyramid from its area requires a few more calculations than simply calculating the measure of the apothem.
If, instead of the lateral area, we are given the volume of a cone or a pyramid and the dimensions of the base, the height can be found directly. This measurement is in the formula for the volume of cones and pyramids. The formula for the volume of these solids is |V= \dfrac{A_b \times h}{3}.|
To find the apothem of one of these solids from the volume, first find the height. Then, use the Pythagorean Theorem to calculate the apothem. Read the concept sheet about finding the measurement of the apothem of a pyramid or a cone for more information.
What is the height of a traditional billiard ball (in millimetres)?
