The Volume of Pyramids

||V = \dfrac{A_b \times h}{3}||

where

||\begin{align} A_b &= \text{Area of a base}\\ h &= \text{height of the pyramid}\end{align}||
 

In Quebec City, part of a commercial building is built like a square pyramid.

To comply with regulations, the pyramid section of the building has a base with a perimeter of |160\ \text{m}| and a height of |15\ \text{m}.|  |70\ \%| of the space is reserved for administrative offices. How much space do the administrative offices occupy?

1. Identify the type of solid 
   It is a square pyramid.

2. Apply the formula
   Since the base is square, we can determine that one side measures |160 \div 4=40\ \text{m}.|
   Thus, ||\begin{align} V &=\dfrac{A_b \times h}{3}\\\\&= \dfrac{s^2\times h}{3} \\\\&= \dfrac{40^2 \times 15}{3}\\\\&= 8\ 000\ \text{m}^3 \end{align}||

3. Interpret the answer
   Since we are interested in |70\ \%| of the space, the following is obtained.
   ||70\ \% \times 8\ 000 = 5\ 600\ \text{m}^3||

   Thus, the administrative offices occupy |5\ 600 \ \text{m}^3.|

Finding the height of a pyramid from the apothem 

In the case of a right pyramid, a right triangle is obtained by drawing the height from the apex and joining it to the centre of the base. This height is called the apothem of the pyramid.

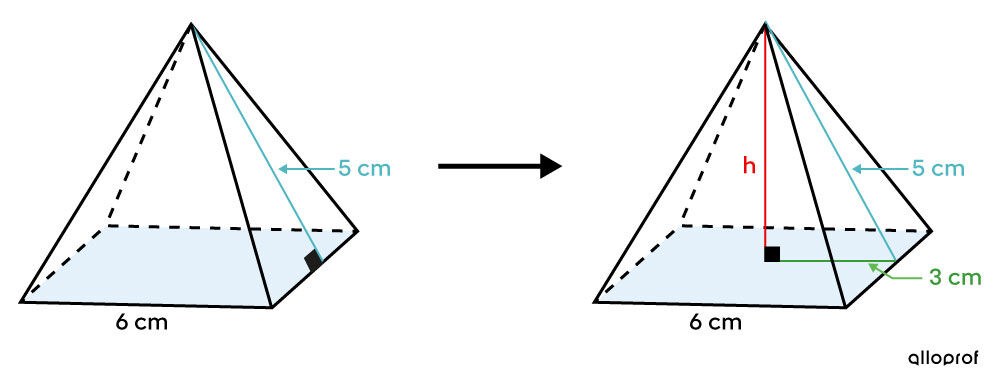
Since the pyramid’s height ends at the centre of its base, and it is a right pyramid, the measurement of the leg is half the measurement of the side of the base.

Associating the measurement of one leg with half of one side of the base, the other leg with the pyramid’s height, and the apothem with the hypotenuse enables us to use the Pythagorean Theorem.

||\begin{align} \color{#3A9A38}{a}^2 + \color{#EC0000}{b}^2 &= \color{#51B6C2}{c}^2\\\\ \color{#3A9A38}{3}^2 + \color{#EC0000}{h}^2 &= \color{#51B6C2}{5}^2\\ \color{#EC0000}{h}^2 &= 16\\ \color{#EC0000}{h} &= 4 \ \text{cm}\end{align}||