Subjects
Grades
The Volume of Cones
Concept sheet | Mathematics
Secondary
3
Table of contents
Although cones are solids with curved surfaces, their volume is calculated the same way as pyramids — except the area of the base will always be that of a circle.
To determine the three-dimensional space occupied by a cone, first consider the area of its base and then multiply it by its height. Finally, divide it by 3.
|V = \dfrac{A_b \times h}{3}| or |V=\dfrac{\pi r^2\times h}{3}|
where
||\begin{align} A_b &= \text{Area of the base}\\ h &= \text{height of the cone}\\ r &= \text{radius of the base}\end{align}||
All drinks in a restaurant are served in glasses of the same size.
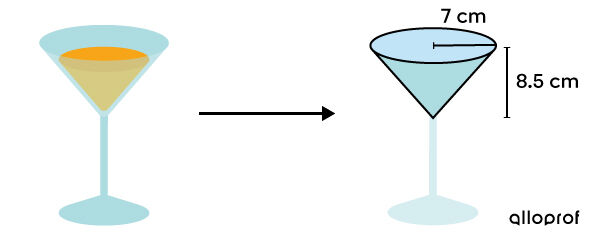
To set the right price for different drinks, determine, in |\text{cm}^3,| the maximum volume of liquid that a glass can hold.
-
Identify the solid
It is a cone with an apex pointing downwards. -
Apply the formula
||\begin{align} V &= \dfrac{A_b \times h}{3}\\\\ &= \dfrac{\pi r^2 \times h}{3} \\\\&= \dfrac{\pi (7)^2 \times 8{.}5}{3}\\\\&\approx 436{.}16 \ \text{cm}^3\end{align}|| -
Interpret the answer
Each glass in this shape can hold a maximum of |436{.}16\ \text{cm}^3| of liquid.
Some problems require finding the measurement of the base or the height of the cone when the volume is given. This is called finding a missing measurement of a cone from a given volume.
Finding the Height of a Cone From the Apothem
Even with all the available formulas, sometimes certain measurements are missing. In these cases, other mathematical concepts must be used to obtain the desired result. For example, the height measurement is not always included. Thus, the Pythagorean Theorem is often used.
Finding the height of a cone from the apothem
In the case of a right cone, a right triangle can be obtained by drawing a line segment from the apex, joining the circle forming the base, the height of the cone, and the radius of the base.
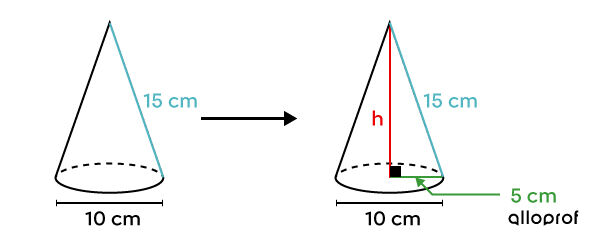
Since the height intercepts the centre of the base and it is a right cone, the horizontal leg measurement is half the measurement of the diameter.
Relating the measurement of one leg with the radius of the base, the other leg with the height of the cone, and the apothem with the hypotenuse enables us to use the Pythagorean Theorem.
||\begin{align}\color{#3A9A38}{a}^2 + \color{#EC0000}{b}^2 &=\color{#51B6C2}{c}^2\\ \color{#3A9A38}{5}^2 +\color{#EC0000}{h}^2 &= \color{#51B6C2}{15}^2\\ \color{#EC0000}{h}^2 &= 200\\ \color{#EC0000}{h} &\approx 14{.}14 \ \text{cm}\end{align}||
Thus, the height of the cone is about |14{.}14 \ \text{cm}.|
If the measurement of the apothem when given the height is sought, the Pythagorean Theorem must be used again.
Vidéo
The Volume of Pyramids and Cones
Moments in the video:
- 00:00-Definition of volume
- 00:17-Volume formula
- 01:28-Volume of a pyramid
- 02:23-Volume of a cone