Matières
Niveaux
Résoudre une équation ou une inéquation sinus
Fiche | Mathématiques
Secondaire
5
Table des matières
- Haut de page
- Résoudre une équation sinus
- Résoudre une équation sinus à l’aide du cercle trigonométrique
- Résoudre une équation sinus à l’aide de |\boldsymbol{\arcsin}|
- Exercice - Résoudre une équation sinus
- Résoudre une équation sinus de degré 2
- Résoudre une inéquation sinus
- Résoudre une inéquation sinus à l’aide du cercle trigonométrique
- Résoudre une inéquation sinus à l’aide de |\boldsymbol{\arcsin}|
- Exercice - Résoudre une inéquation sinus
- Résoudre une inéquation sinus de degré 2
- À voir aussi
Une équation ou une inéquation sinus contient un rapport sinus, où l’inconnue |(x)| apparait dans l’argument.
Puisque la fonction sinus est périodique, ce type d’équation peut ne posséder aucune solution, peut posséder une solution, plusieurs solutions ou une infinité de solutions.
De plus, il est nécessaire d’utiliser les angles en radians.
Dans le cercle trigonométrique, le sinus d’un angle correspond à l’ordonnée du point sur le cercle. Lorsqu’on résout une équation sinus, on cherche les angles qui possèdent une certaine ordonnée. Pour y arriver, on peut utiliser les points remarquables du cercle trigonométrique ou la fonction réciproque |\boldsymbol{\arcsin}.|
Lorsqu’on utilise le cercle trigonométrique, on choisit généralement des angles compris entre |0| et |2\pi.|
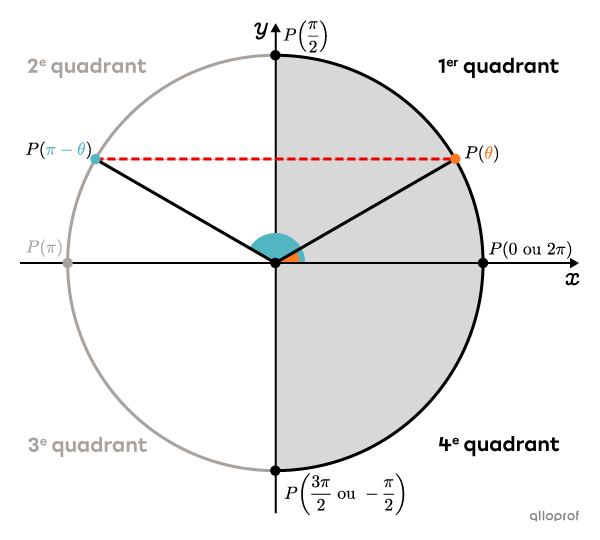
Lorsqu’on utilise la fonction réciproque |\arcsin,| le résultat obtenu est toujours un angle situé dans le 1er quadrant ou dans le 4e quadrant du cercle trigonométrique. Autrement dit, l’angle est compris entre |-\dfrac{\pi}{2}| et |\dfrac{\pi}{2}.|
Or, il y a toujours 2 angles trigonométriques différents qui possèdent la même ordonnée. C’est pourquoi, à partir de l’angle obtenu |\boldsymbol{\color{#fa7921}{(\theta)}},| on obtient le 2e angle en faisant |\boldsymbol{\color{#51b6c2}{\pi-\theta}}.|
La fonction réciproque |\arcsin| est parfois notée |\sin^{-1},| notamment sur les calculatrices.
Résoudre une équation ou une inéquation sinus
Résoudre une équation sinus
La démarche à suivre pour résoudre une équation sinus est la suivante.
-
Isoler le rapport sinus.
-
Déterminer les angles trigonométriques.
- Si le rapport sinus est égal à une coordonnée de points remarquables, utiliser le cercle trigonométrique.
- Sinon, utiliser la fonction réciproque |\boldsymbol{\arcsin}.| -
Résoudre les équations obtenues avec les angles trigonométriques.
-
Calculer la période de la fonction sinus.
-
Donner les solutions de l’équation.
Résoudre une équation sinus à l’aide du cercle trigonométrique
Voici un exemple où on utilise les points remarquables du cercle trigonométrique pour résoudre l’équation.
Résous l’équation suivante.||-\sin(x)-\dfrac{\sqrt{2}}{2}=0||
Résoudre une équation sinus
Voir la solution
Résoudre une équation sinus à l’aide de |\boldsymbol{\arcsin}|
Voici un exemple où on utilise la fonction réciproque arc sinus pour résoudre l’équation.
Résous l'équation suivante dans l’intervalle |[0,2\pi].|||\sin\!\big(2(x-3)\big)-1=-\dfrac{1}{3}||
Voir la solution
Exercice - Résoudre une équation sinus
Résoudre une équation sinus de degré 2
Voici un exemple où on résout une équation sinus de degré 2.
Résous l'équation suivante.||2\sin^2\left(\dfrac{x+\pi}{3}\right)-\sin\left(\dfrac{x+\pi}{3}\right)-1=0||
Voir la solution
Résoudre une inéquation sinus
La démarche à suivre pour résoudre une inéquation sinus est la suivante.
-
Changer le symbole d’inégalité par un symbole d’égalité.
-
Isoler le rapport sinus.
-
Déterminer les angles trigonométriques.
- Si le rapport sinus est égal à une coordonnée de points remarquables, utiliser le cercle trigonométrique.
- Sinon, utiliser la fonction réciproque |\boldsymbol{\arcsin}.| -
Résoudre les équations obtenues avec les angles trigonométriques.
-
Calculer la période de la fonction sinus.
-
Donner l’ensemble-solution de l’inéquation.
Résoudre une inéquation sinus à l’aide du cercle trigonométrique
Voici un exemple où on utilise les points remarquables du cercle trigonométrique pour résoudre l’inéquation.
Résous l'inéquation suivante.||4\sin(4x)+3>5||
Voir la solution
Résoudre une inéquation sinus à l’aide de |\boldsymbol{\arcsin}|
Voici un exemple où on utilise la fonction réciproque arc sinus pour résoudre l’inéquation.
Résous l'inéquation suivante.||-10\sin\left(\dfrac{2(x-1)}{3}\right)+4\ge12||
Résoudre une inéquation sinus
Voir la solution
Exercice - Résoudre une inéquation sinus
Résoudre une inéquation sinus de degré 2
Voici un exemple où on résout une inéquation sinus de degré 2.
Résous l’inéquation suivante.||\sin^2(x)<\dfrac{3}{4}||