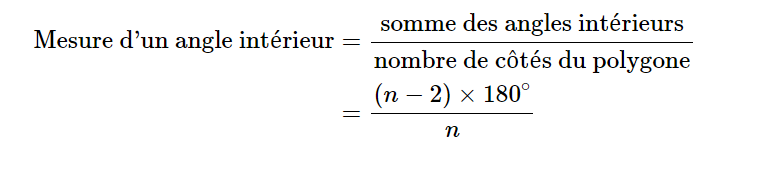Best Of

Bonjour TortueOrange9884! :)

Merci pour ta question!

En regardant ton devoir, on comprend que l’objectif est de vérifier si la sculpture peut entrer dans la boîte. Pour cela, il faut s’assurer que :

• la hauteur totale de la sculpture est inférieure à 33,5 cm
• le diamètre total est inférieur à 16 cm

Pour y arriver, voici les étapes que je te conseille de suivre :

1. Choisir un rayon possible pour le cylindre A

On nous dit que le rayon du cylindre A peut être de 4 cm, 5 cm ou 6 cm. Il faut en choisir un (ex. : 4 cm) et l’utiliser pour faire tes calculs.

2. Trouver la hauteur du cylindre A

Utilise la formule du volume d’un cylindre :

V=πr²h

Tu connais le volume (800 mL, donc 800 cm³) et tu viens de choisir le rayon. Tu peux donc isoler le h!

3. Trouver la hauteur du cône

Le cône a le même rayon que le cylindre A et un volume de 500 cm³. Utilise la formule du volume d’un cône :

V=πr²h/3

Encore une fois, tu connais le volume et le rayon, donc tu peux isoler la hauteur!

4. Calculer les dimensions du cylindre B

Le cylindre B a un rayon égal au rayon du cylindre A + 2 cm.

Tu dois choisir une hauteur pour le cylindre B qui respecte ces trois critères :

• Son volume doit être un multiple de 100
• Il doit être plus grand que le volume du cône (500 cm³)
• Il doit être plus petit que le volume du cylindre A (800 cm³)

Utilise à nouveau la formule V=πr² pour essayer différentes hauteurs et trouver un bon volume!

Finalement, une fois que nous avons trouvé les données, il nous reste qu'à additionner les hauteurs des 3 parties et s'assurer que la hauteur ne dépasse pas 33.5 cm et que le diamètre est inférieure à 16 cm.

Si nous respectons ces critères, la sculpture peut entrer dans la boite!

J'espère avoir répondu à ta question! Si tu as d'autres questions, n'hésite pas à revenir nous voir!

Passe une bonne journée! :)

Salut!

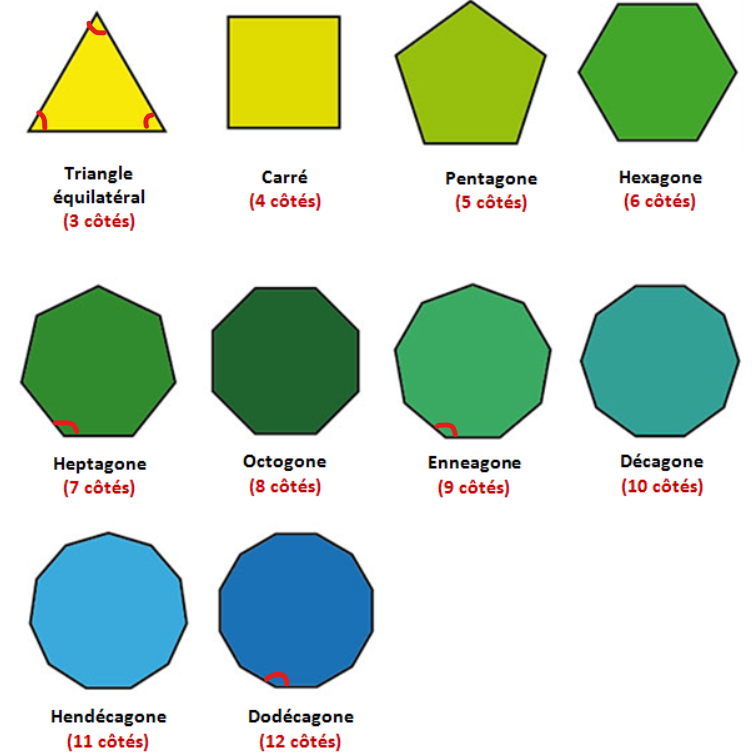
Il est impossible qu'un polygone n'ait pas d'angles intérieurs! ;)

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Une figure qui n'a pas d'angles du tout n'est pas un polygone, mais un cercle!

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

J'espère que c'est plus clair pour toi! :)

Allo CoccinelleTurquoise8432!

Pour répondre à ta question, il est impossible pour un polygone de ne pas avoir d'angles.

En revanche, un polygone est convexe lorsque tous ses angles sont inférieurs à 180°. Autrement dit, il n'a aucun angle rentrant.

Un polygone non-convexe est l'inverse d'un polygone convexe, c'est-à-dire qu'il a AU MOINS UN angle rentrant, ou supérieur à 180°.

En espérant que cela t'aides un peu!

QuartzMauve1105

Salut!

Pour résoudre une équation contenant des expressions algébriques, tu dois toujours placer les termes semblables d'un côté de l'équation, et les constantes de l'autre côté. Prenons un exemple pour mieux comprendre.

On a l'équation :

$$ \frac{3x}{4} - \frac{6}{7} = \frac{2x}{3} + \frac{3}{14} $$

Les termes semblables sont les termes ayant les mêmes variables (les mêmes inconnus). et ces variables sont affectées des mêmes exposants. Donc, nos termes semblables sont ici \(\frac{3x}{4} \) et \( \frac{2x}{3}\), puisqu'ils contiennent tous les deux la variable x affectée d'un exposant 1.

Les constantes sont les termes qui ne contiennent pas de variables, soit ici \(- \frac{6}{7}\) et \(\frac{3}{14} \).

Notre but sera d'abord de placer d'un côté de l'égalité les deux termes semblables, et de l'autre côté les constantes. Pour ce faire, nous allons commencer par déplacer un des deux termes semblables de l'autre côté (peu importe lequel), et ce, en effectuant l'opération inverse.

Déplaçons \( \frac{2x}{3}\) du côté gauche de l'égalité. Puisque l'opération inverse d'une addition est une soustraction, nous allons devoir soustraire \( \frac{2x}{3}\) de chaque côté de l'équation, comme ceci :

$$ \frac{3x}{4} - \frac{6}{7} = \frac{2x}{3} + \frac{3}{14} $$

$$ \frac{3x}{4} - \frac{6}{7} - \frac{2x}{3} = \frac{2x}{3} + \frac{3}{14} - \frac{2x}{3} $$

En le soustrayant de chaque côté, cela nous permet de l'éliminer du côté droit de l'équation :

$$ \frac{3x}{4} - \frac{6}{7} - \frac{2x}{3} = \frac{3}{14} $$

On a ainsi déplacé le terme \( \frac{2x}{3}\) afin qu'il soit du même côté que son terme semblable.

Passons maintenant aux constantes. Nous allons déplacer la constante \(\frac{6}{7}\) de l'autre côté. Puisque l'opération inverse d'une soustraction est une addition, nous allons donc additionner \(\frac{6}{7}\) de chaque côté :

$$ \frac{3x}{4} - \frac{6}{7} - \frac{2x}{3} + \frac{6}{7}= \frac{3}{14}+\frac{6}{7} $$

$$ \frac{3x}{4}- \frac{2x}{3}= \frac{3}{14}+\frac{6}{7} $$

On a ainsi réussi à placer nos termes semblables d'un côté et nos constantes de l'autre! La prochaine étape sera d'additionner les constantes, et d'additionner les coefficients des termes semblables. Pour cela, il faudra placer les fractions sur un même dénominateur.

Commençons par les constantes. On a les dénominateurs 14 et 7, il faut donc trouver le PPCM de 14 et 7, qui est 14. On peut alors transformer la fraction \(\frac{6}{7} \) en une fraction équivalente donc le dénominateur sera 14.

$$ \frac{6}{7} = \frac{?}{14} $$

Puisqu'on doit multiplier le dénominateur 7 par 2 pour obtenir 14, il faut alors aussi multiplier le numérateur 6 par 2 :

$$ \frac{6}{7} = \frac{6\times2}{7\times 2}=\frac{12}{14} $$

On remplace alors \(\frac{6}{7} \) par sa fraction équivalente dans l'équation :

$$ \frac{3x}{4}- \frac{2x}{3}= \frac{3}{14}+\frac{12}{14} $$

Maintenant que les deux fractions sont sur le même dénominateur, on peut additionner leur numérateur :

$$ \frac{3x}{4}- \frac{2x}{3}= \frac{3+12}{14} $$

$$ \frac{3x}{4}- \frac{2x}{3}= \frac{15}{14} $$

On suit le même principe pour les termes semblables. Il faut placer les fractions \(\frac{3}{4}\) et \(\frac{2}{3}\) sur un même dénominateur. Pour cela, on cherche le PPCM de 4 et 3, soit 12. Il faut alors transformer les deux fractions en des fractions équivalentes dont le dénominateur est 12 :

$$ \frac{3}{4}x- \frac{2}{3}x= \frac{15}{14} $$

$$ \frac{3\times3}{4\times3}x- \frac{2\times4}{3\times4}x= \frac{15}{14} $$

$$ \frac{9}{12}x- \frac{8}{12}x= \frac{15}{14} $$

On peut maintenant soustraire les numérateurs des deux fractions :

$$ \frac{9-8}{12}x= \frac{15}{14} $$

$$ \frac{1}{12}x= \frac{15}{14} $$

Finalement, la dernière étape sera d'éliminer le coefficient de la variable x, soit \(\frac{1}{12}\), et ce, en effectuant l'opération inverse d'une multiplication, soit une division :

$$ \frac{1}{12}x \div \frac{1}{12}= \frac{15}{14} \div \frac{1}{12} $$

$$x= \frac{15}{14} \div \frac{1}{12} $$

Lorsqu'on divise par une fraction, c'est l'équivalent de multiplier par l'inverse de cette fraction :

$$x= \frac{15}{14} \times \frac{12}{1} $$

On peut maintenant multiplier les numérateurs et les dénominateurs ensemble :

$$x= \frac{15\times 12}{14\times 1} $$

$$x= \frac{180}{14} $$

Voilà! Cependant, la réponse n'est pas une fraction irréductible, il faut donc la simplifier. Pour ce faire, on doit diviser le numérateur et le dénominateur par le PGCD de 180 et 14, soit 7 :

$$x= \frac{180\div 2}{14\div 2} $$

$$x= \frac{90}{7} $$

Tu peux laisser ta réponse finale sous forme de fraction impropre comme celle-ci (le numérateur est supérieur au dénominateur), ou tu peux la transformer en un nombre fractionnaire ou un nombre décimal, il faudra alors vérifier ce que l'exercice ou ton professeur te demandera de faire.

Si la variable x était plutôt au dénominateur, alors tu peux utiliser la technique du produit croisé afin de la ramener au numérateur, puis suivre la démarche présentée précédemment. Voici un exemple :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Tu pourrais aussi multiplier chaque côté de l'équation par la variable x, ce qui permettra de ramener la variable x au numérateur. Voici un exemple :

$$ \frac{3}{4x} - \frac{6}{7} = \frac{2x}{3} + \frac{3}{14} $$

$$ \frac{3}{4x}- \frac{2x}{3}= \frac{3}{14}+\frac{6}{7} $$

$$ \frac{3}{4x}- \frac{2x}{3}= \frac{15}{14}$$

On multiplie tous les termes par x :

$$x \times( \frac{3}{4x}- \frac{2x}{3})= x\times (\frac{15}{14})$$

$$ \frac{3}{4}- \frac{2x^2}{3}= \frac{15x}{14}$$

On a ainsi éliminé la variable x du dénominateur! Or, dans cet exemple, on a maintenant une équation de second degré. On peut donc déplacer tous les termes du même côté :

$$0= \frac{2}{3}x^2+ \frac{15}{14}x-\frac{3}{4}$$

Puis, on peut utiliser la formule quadratique pour la résoudre.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Voici des fiches sur ces notions qui pourraient t'être utiles :

• La résolution d'équations et d'inéquations | Secondaire | Alloprof
• Résoudre une équation ou une inéquation rationnelle | Secondaire | Alloprof
• Résoudre une équation ou une inéquation de degré 2 | Secondaire | Alloprof

J'espère que c'est plus clair pour toi! Sinon, n'hésite pas à nous réécrire! :)

Salut FraiseTurquoise2087!😊

Tu as eu la bonne réponse pour Toronto! Toutefois, je remarque que les nombres négatifs sont un petit peu plus tannants. Mais je vois que tu comprends bien les additions et soustractions. Le seul défi est de voir quand faire une soustraction et quand faire une addition! Si le nombre est négatif, tu dois le soustraire au nombre positif.

Pour te pratiquer, je te suggère notre jeu Météormath! Tu vas devenir ou ou une vrai pro🔥

Voici le lien : https://www.alloprof.qc.ca/fr/eleves/bv/jeux/meteormath-2

Bonjour, ChevalSympathique8993!

La règle d'une suite arithmétique peut s'écrire sous la forme suivante.

$$ \text{Terme = régularité} \times \text{rang du terme + terme de rang zéro} $$

On peut aussi écrire cette formule en utilisant une forme abrégée.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Pour trouver la règle d'une suite arithmétique, il faut utiliser la démarche suivante.

1. Déterminer la régularité en calculant la différence entre 2 termes consécutifs.
2. Déterminer la valeur du terme lorsque le rang est égal à 0 (rang 0).
3. Écrire la règle de la suite.

Voyons un exemple.

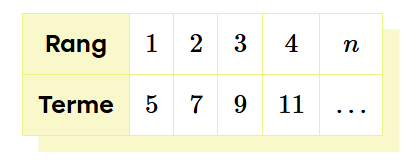
Prenons la table de valeurs suivante.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

1) Déterminer la régularité

La distance entre 2 termes consécutifs représente la régularité de la règle.

\begin{align}7-5 &=2\\ 9-7&=2 \\ 11-9 &= 2\end{align}

La régularité est donc de +2.

On peut donc écrire t = 2 x n + rang 0.

2) Déterminer la valeur du rang 0

On peut déterminer la valeur du terme qui serait situé au rang 0.

Pour ce faire, il faut soustraire la régularité au terme situé au rang 1.

5−(+2)=3

Le rang 0 est donc 3.

3) Écrire la règle

La règle est donc la suivante.

t=2n+3

N'hésite pas à poser d'autres questions!

Salut!

Voici la formule permettant de calculer la mesure d'un angle intérieur de n'importe quel polygone régulier :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ainsi, si on connait la mesure d'un angle intérieur, il ne reste plus qu'à isoler la variable \(n\) dans la formule pour trouver le nombre de côtés, et donc le type de polygone (pentagone, hexagone, heptagone, etc.)

Par exemple, si un polygone convexe a un angle intérieur de 135 degrés, voici le calcul permettant de trouver son nombre de côtés :

$$ 135 = \frac{(n-2)\times180}{n}$$

$$ 135 \times n= \frac{(n-2)\times180}{n}\times n$$

$$ 135n= (n-2)\times180$$

$$ 135n= 180n - 360$$

$$ 135n-180n= 180n - 360 -180n$$

$$ -45n= - 360 $$

$$ \frac{-45n}{-45}= \frac{- 360}{-45} $$

$$ n = 8 $$

On trouve donc qu'il s'agit d'un octogone (8 côtés)!

N'hésite pas si tu as d'autres questions! :)

L’ algèbre est la branche des mathématiques qui généralise les règles de calculs arithmétiques à l’aide de variables. Une expression algébrique est un ensemble de termes algébriques et constants reliés entre eux par des additions (+) (+) et des soustractions (−). (−).