Subjects
Grades
Missing Measures from a Volume: Decomposable and Truncated Solids
Concept sheet | Mathematics
Secondary
2-3
To successfully calculate a missing measure in a decomposable or truncated solid from the volume, we must create an equation and solve it. To do so, the formulas that enable us to calculate the volume of solids are used. The following is an overview of the process.
-
Determine the volume with which we must work.
-
Identify the missing measurement by using a variable.
-
Associate the volume of each solid with a numerical value or an algebraic expression.
-
Create an equation based on the context.
-
Solve the equation.
-
Interpret the answer according to the context.
Finding a Missing Measure from a First-Degree Equation
When closed, a lunch box looks like the following.
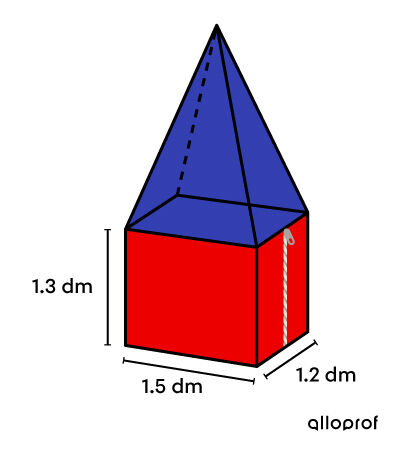
On average, the space available inside a lunch box is |3.65\ \text{dm}^3.| What should be the total height of the lunchbox to respect the standard?
See solution
Finding a Missing Measure from a Second-Degree Equation
To find a missing measure from the volume of complex solids with 2nd degree equations, the approach is relatively similar to the one involving 1st degree equations. However, the methods for solving them may include factoring with the product-sum method or applying the quadratic formula.
To give a nice shape to various robot toys, they must be adequately stuffed. We use a synthetic material that sells for |$2/\text{dm}^3.| to shape it. To make the final selling price of the product affordable to the maximum number of people possible, we want to limit the cost of stuffing to |$5.60\ | per toy robot.
This model’s head is a cube, the body is a prism with a trapezoidal base, the legs are rectangular-based prisms and the arms are cylinders.
Based on the information in the illustration, how thick should the arms be?
See solution
Finding a Missing Measure in a Truncated Solid
A truncated solid is a solid where a portion has been removed. Thus, to find a missing measure in a truncated solid, one must consider the original solid and subtract appropriately.
To improve its brand, a company wants to change the shape of an orange juice carton. However, the company wants the new model to be based on the old one. Thus, the red section was obtained by horizontally truncating the pink pyramid of the old model. Finally, the total height of the carton remains the same, i.e., |21\ \text{cm}.|
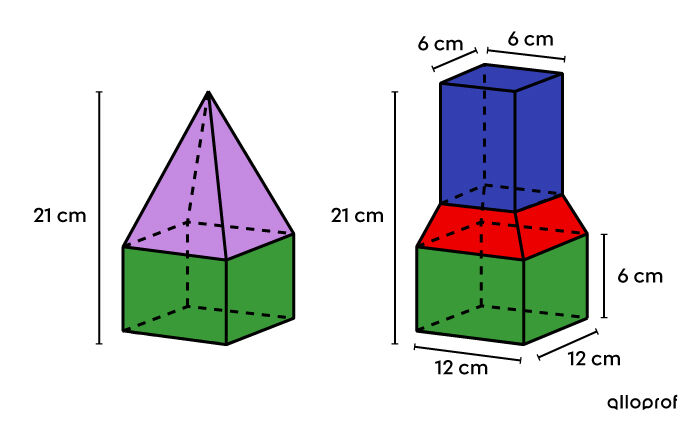
Based on the information provided in the drawing, what should be the height measurement of the new container’s top since the new model’s volume is |1\ 872\ \text{cm}^3?|
See solution
Finding a Missing Measure in a Decomposable Solid
A decomposable solid is a solid that can be separated into several simpler solids. To find a missing measure in a decomposable solid, we usually decompose it by identifying individual solids and subtracting the ones that are removed.
With Christmas approaching, a new product is arriving on the market. It is a cubic-shaped snow globe made of glass. Inside is a cylindrical cavity where you insert a photo of a loved one.
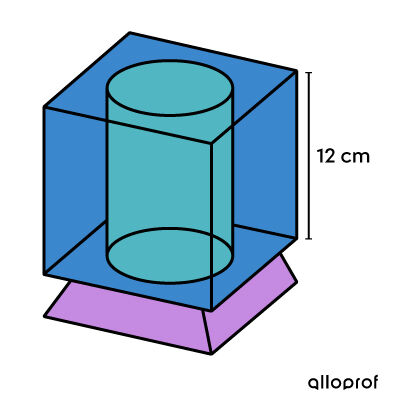
To ensure the movement of the artificial snowflakes in the enclosed section of the cube, it is filled |90\ \%| with a liquid, representing |1.010 \, 7\ \text{L}| of liquid. Based on the information, determine the diameter of the product’s cylindrical cavity.