Subjects
Grades
Missing Measurements of Solids from the Volume
Concept sheet | Mathematics
Secondary
3
Table of contents
- Top of page
- Finding the Missing Measurement of a Cube
- Finding the Missing Measurement of a Prism
- Finding the Missing Measurement of a Cylinder
- Finding the Missing Measurement of a Sphere
- Finding the Missing Measurement of a Pyramid
- Finding the Missing Measurement of a Cone
- Finding the Measurement of the Apothem of a Pyramid or a Cone
- See also
- Exercise
Sometimes, we are given a solid’s volume and all but one of its measurements. So, it is necessary to know how to find a missing measurement.
The procedure for finding a missing measurement in a solid is generally the same regardless of the type of solid. Here are the main steps.
-
Identify the measurements given.
-
Determine the formula to use.
-
Replace the variables with the given measurements.
-
Isolate the sought variable.
Finding the Missing Measurement of a Cube
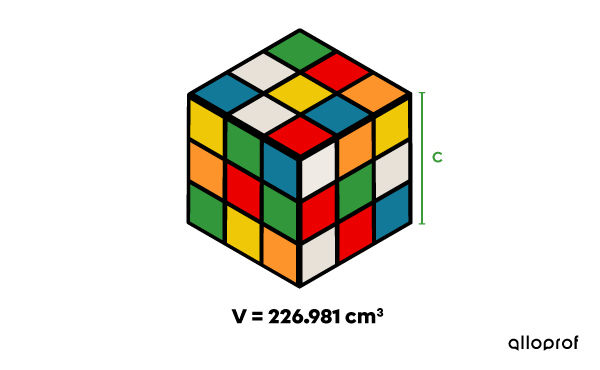
You keep a Rubik's Cube in your backpack to pass the time during breaks at school. With all the school books and supplies you have in your bag, there is only 226.981 cm3 left for the Rubik's Cube.
What should be the maximum measurement of the Rubik's Cube’s edge for it to fit into your backpack?
See solution
Finding the Missing Measurement of a Prism
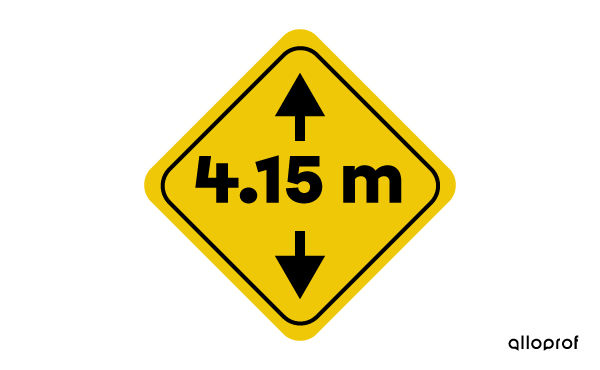
Bobby, a trucker, checks his routes beforehand for the height of the overpasses to avoid damaging his truck and the goods he is transporting. While driving with a big load, he sees the sign below.
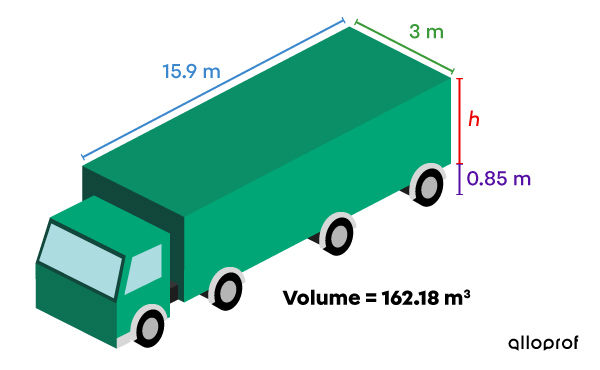
Bobby only knows the volume of the trailer behind his truck, so he stops on the side of the road to check that his truck is not too high to drive under the next overpass.
Since it is impossible for him to reach the top of his truck, what calculations can he use to determine the height of his trailer?
See solution
Finding the Missing Measurement of a Cylinder
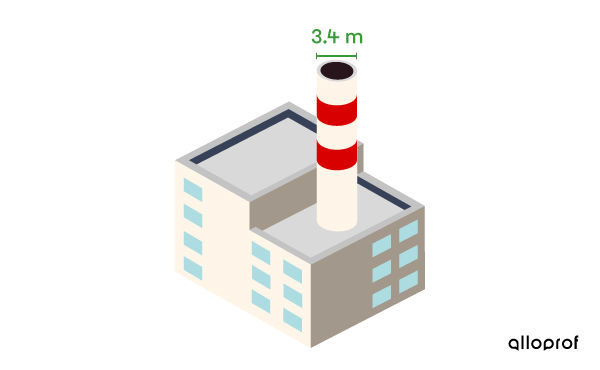
To ensure the effectiveness of air filters, production plants must ensure that their stacks do not contain more than 385 m3 of waste gas.
Based on the building plans, what should the minimum height of the cylindrical chimney be?
See solution
Finding the Missing Measurement of a Sphere
Before playing a game of Bubble soccer, you have to put on some special equipment. In fact, players must wear a huge spherical protective bubble so that they can safely collide with other players.
The only downside is that participants must be at least as tall as the height of the protective bubble. If the volume of a protective bubble is 1.44 m3, what should be the minimum height of the participants?
See solution
Finding the Missing Measurement of a Pyramid
It took 2 592 341 m3 of stone to build the Pyramid of Cheops in Egypt, which is a regular square-based pyramid whose base sides measure 230 m each. What is the pyramid’s height?
The Pyramid of Cheops
Source : kallerna, wikipedia.org
See solution
Finding the Missing Measurement of a Cone
A restaurant owner wants to determine the exact diameter of the drinking glasses in order to ensure a good profit margin.
One drink is usually equivalent to 90 mL, or 90 cm3. To respect this quantity, what diameter should the glass be, considering that the thickness of the glass is negligible?
See solution
Sometimes, the measure of the apothem of a pyramid or cone must be determined from the volume – even though it is not found in the volume formula. In such cases, find the solid’s height or the base’s radius then calculate the measure of the apothem using the Pythagorean Theorem.
Finding the Measurement of the Apothem of a Pyramid or a Cone
The same process is used to find the measurement of the apothem of a cone or a pyramid. The cone is presented in the following example.
To prevent a cone-shaped tent from blowing away in the wind, anchoring cords connect the tent’s apex to the ground using stakes. These safety cords must run along the tent’s walls.
Using the information provided in the figure below, and knowing that an additional 30 cm must be left at both ends of each anchoring cord for a knot, what is the minimum length of one of the safety cords?
See solution
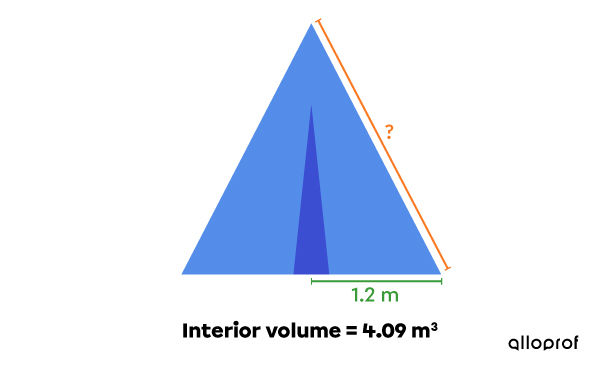
The previous example shows that we must find the measure of the height before using the Pythagorean Theorem to determine the measure of the apothem. Using the volume to find the measure of a cone or pyramid's apothem requires a few more calculations than simply finding the height.
If we know the lateral area of a cone or a pyramid and the dimensions of the base instead of its volume, the measure of the apothem can be found directly. We can find this measurement in the formula for the lateral area of cones and pyramids: |A_L = \dfrac{P_b \times a}{2}.|
If the height of one of these solids must be found using the lateral area, begin by finding the measure of the apothem. Next, use the Pythagorean Theorem to find the height. Read the concept sheet about finding the measurement of the height of a pyramid or a cone for more information.