L'aire des solides tronqués

Un solide tronqué​​ est un solide qui a été coupé par un plan et dont seulement une portion de la séparation a été conservée. Ce plan de coupe peut être parallèle à la base de ce dernier ou non.

​​ Voici une illustration représentant des cônes tronqués par un plan.

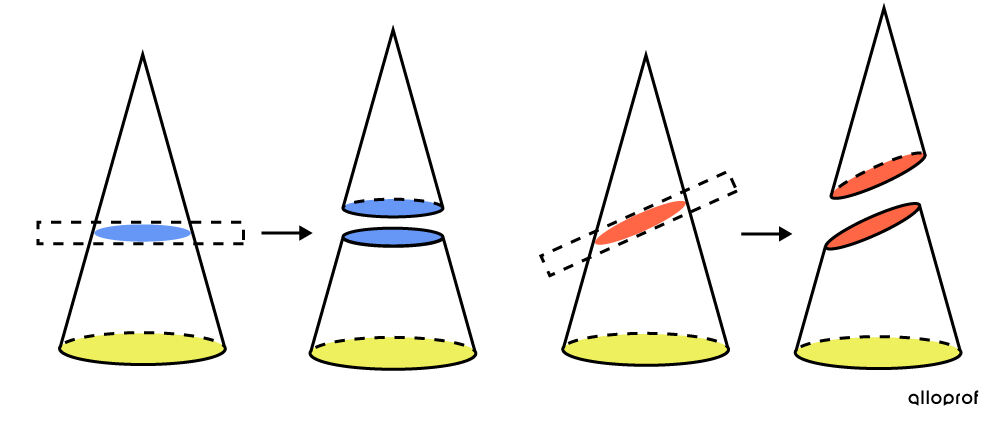
Dans ce dessin, on voit que le premier couple de cônes est créé selon un plan qui e​st parallèle à la base du cône. C’est ce genre de cônes tronqués qui est étudié dans la présente fiche. Or, dans le deuxième couple de cônes, le plan n'est pas parallèle à la base du cône.​ Ce cas n’est pas à l'étude ici. 
 

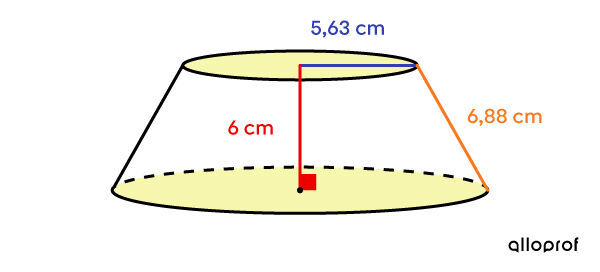
​Quelle est l'aire totale du cône tronqué suivant en sachant que le rayon, la hauteur et l'apothème qui lui sont associés mesuraient respectivement 9 cm, 16 cm et 18,36 cm?

1. Calculer l'aire des bases
   Dans ce cas, les bases sont deux disques dont la mesure du rayon est différente.

||\begin{align} A_\text{petite base} &= \pi \color{#333FB1}{r}^2 \\ &= \pi (\color{#333FB1}{5{,}63})^2 \\ &\approx 99{,}58\ \text{cm}^2 \end{align}||

||\begin{align} A_\text{grande base} &= \pi \color{#333FB1}{r}^2\\ &= \pi (\color{#333FB1}{9})^2 \\ &\approx 254{,}47\ \text{cm}^2 \end{align}||

||\begin{align} A_\text{bases} &= 99{,}58 + 254{,}47 \\ &= 354{,}05\ \text{cm}^2 \end{align}||

2. Identifier les solides
   Pour faciliter le reste de la démarche, il est essentiel de bien identifier les solides mis en relation. Dans ce cas, ce sont des cônes qui sont impliqués.

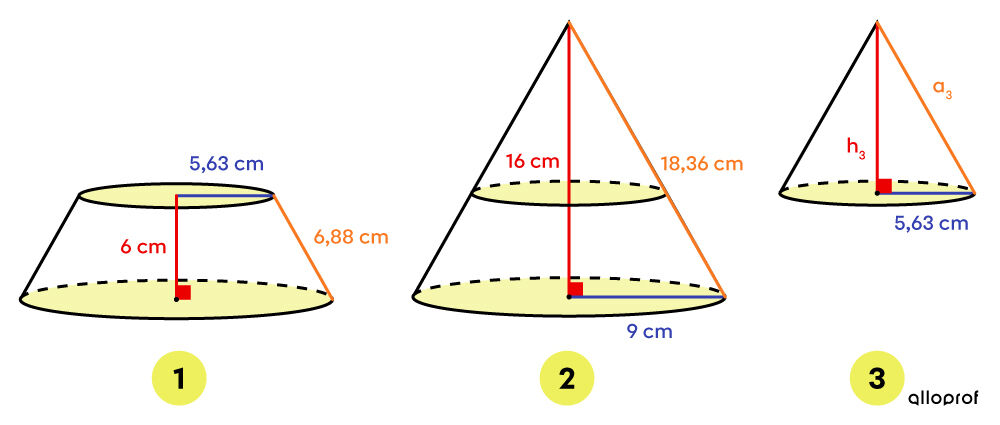
3. Calculer l'aire latérale
   Il faut déterminer la mesure de l'apothème du cône retiré (figure 3). Pour ce faire, on procède par soustraction. ||\begin{align} a_3 &= a_2 - a_1 \\ &= 18{,}36 - 6{,}88 \\ &= 11{,}48 \ \text{cm} \end{align}|| En se fiant aux solides de l'étape précédente, on peut déduire que : ||\begin{align} A_{L1} &= A_{L2} - A_{L3}\\ &= \pi r_2 a_2 - \pi r_3 a_3 \\ &= \pi (9) (18{,}36) - \pi (5{,}63) (11{,}48) \\ &\approx 316{,}07 \ \text{cm}^2 \end{align}||

4. Calculer l'aire totale ||\begin{align} A_T &= A_L + A_\text{bases}\\ &\approx 316{,}07 +354{,}05\\ &\approx 670{,}12 \ \text{cm}^2 \end{align}||​

5. Interpréter la réponse​ 
   L'aire totale de ce cône tronqué est d'environ |670{,}12\ \text{cm}^2.|

​Ariane veut emballer le cadeau qu’elle a acheté pour sa petite sœur. La boite, illustrée ci-dessous, a la forme d’une pyramide tronquée.

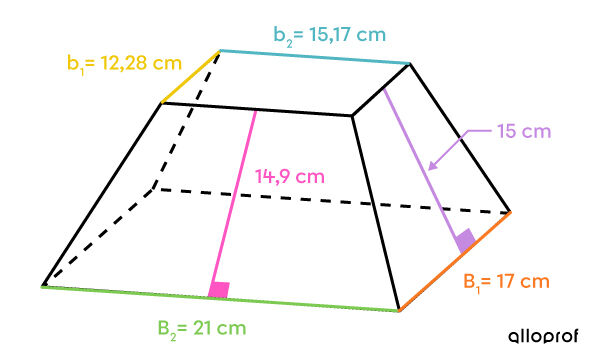
De quelle surface de papier cadeau Ariane aura-t-elle besoin au minimum pour emballer le présent?

1. Calculer l’aire des bases
   Les deux bases sont des rectangles de mesures différentes.

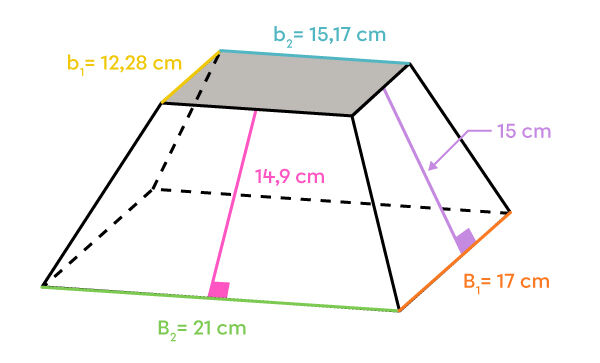
||\begin{align} A_\text{petite base} &= \color{#51b6c2}{b} \times \color{#efc807}{h} \\ &= \color{#51b6c2}{15{,}17} \times \color{#efc807}{12{,}28} \\ &\approx 186{,}29\ \text{cm}^2 \end{align}||

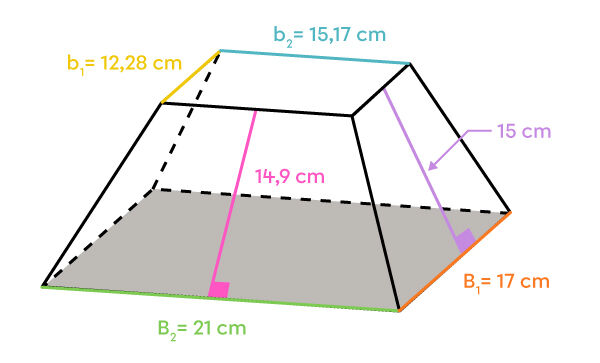
||\begin{align} A_\text{grande base} &= \color{#7cca51}{b} \times \color{#fa7921}{h} \\ &= \color{#7cca51}{21} \times \color{#fa7921}{17} \\ &= 357\ \text{cm}^2 \end{align}||

||\begin{align} A_\text{bases} &= 186{,}29 + 357 \\ &= 543{,}29\ \text{cm}^2 \end{align}||

2. Calculer l’aire latérale
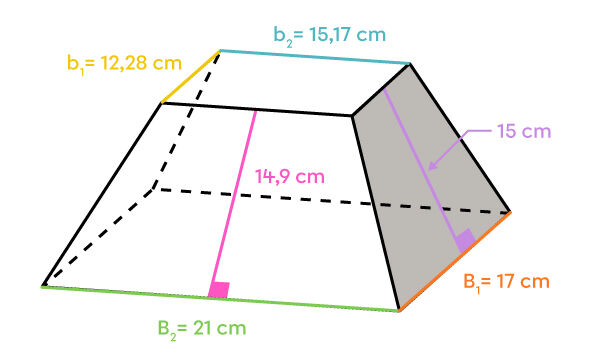
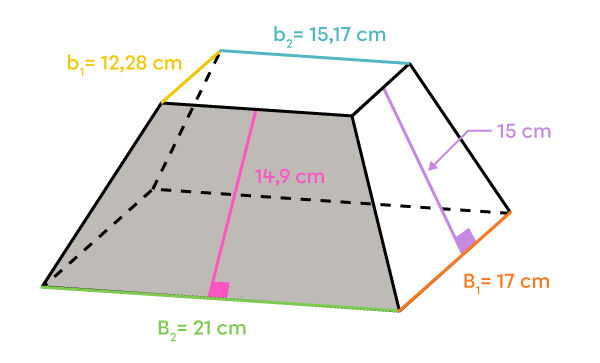
   L’aire latérale est composée de 2 paires de trapèzes isocèles.

||\begin{align}A_\text{petit trapèze} &= \dfrac{(\color{#fa7921}{B_1}+ \color{#efc807}{b_1}) \times \color{#c58ae1}{h}}{2}\\ &=\dfrac{(\color{#fa7921}{17}+ \color{#efc807}{12{,}28}) \times \color{#c58ae1}{15}}{2}\\ &= 219{,}6\ \text{cm}^2\end{align}||

||\begin{align}A_\text{grand trapèze} &= \dfrac{(\color{#7cca51}{B_2}+ \color{#51b6c2}{b_2}) \times \color{#ff55c3}{h}}{2}\\ &=\dfrac{{(\color{#7cca51}{21}+ \color{#51b6c2}{15{,}17})} \times \color{#ff55c3}{14,9}}{2}\\ &\approx{269{,}47}\ \text{cm}^2\end{align}||

||\begin{align} A_\text{L} &= {2}\times{A_\text{petit trapèze}} +{2}\times{A_\text{grand trapèze}}  \\ &= {2}\times{219{,}6} +{2}\times{269{,}47}\\&= 978{,}14\ \text{cm}^2 \end{align}||

3. Calculer l’aire totale
   ||\begin{align} A_T &= A_\text{bases} + A_L\\ &= 543{,}29 +978{,}14\\ &= 1\ 521{,}43 \ \text{cm}^2 \end{align}||​

4. Interpréter la réponse
   Ariane aura besoin, au minimum, de |1\ 521{,}43\ \text{cm}^2| de papier cadeau pour emballer le présent de sa petite sœur.