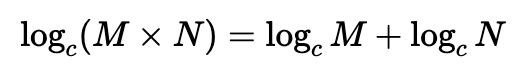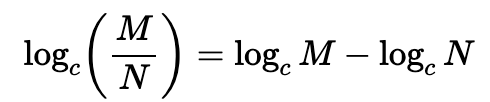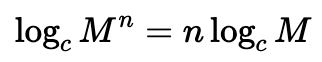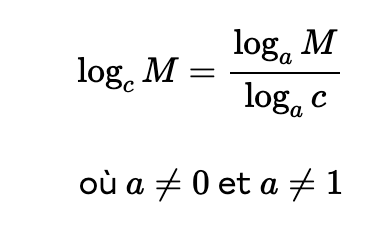Best Of
Re: Question
Bonjour, LynxEfficace6931! :)
Merci pour ta question.
Au début du 19e siècle, on assiste à un déclin du commerce des fourrures, mais une énorme expansion du commerce du bois : le bois devient le principal produit exporté de la colonie.
En agriculture, le Haut-Canada prospère davantage que le Bas-Canada, qui connait une importante crise agricole dans les années 1830.
Ainsi, le commerce des fourrures (bien qu'il soit moins populaire), le commerce du bois et l'agriculture sont trois des principales activités économiques de ces années.
Voici quelques fiches sur l'économie du Canada de 1791 à 1840:
- Capitaux et infrastructures (1791-1840)
- Agriculture (1791-1840)
- Commerce des fourrures (1791-1840)
- Commerce du bois (1791-1840)
Voilà, n'hésite pas à nous réécrire si tu as d'autres questions! :)
Iris
Re: Question
Bonjour,
Merci pour ta question!
Il faut comprendre que le but d'une veste de flottaison est de flotter. Ainsi, pour le a) il faut que tu choisisses le matériau qui est le plus susceptible de te faire flotter dans l'eau.
Pour le b), il faut se demander la question suivante : quelle propriété des matériaux doit-on prendre en compte pour déterminer le meilleur matériau pour flotter? Par élimination, tu devrais être en mesure de trouver la bonne réponse.
Pour le c), tu dois mentionner si la caractéristique choisie te permet d'identifier le matériau en question, c'est-à-dire si la propriété est caractéristique. Je te laisse réfléchir un peu!
Voici deux fiches qui pourraient t'aider :
N'hésite pas si tu as d'autres questions!
Zachary T. :)
Re: Question
Bonsoir MercureNoble8033 😊
Ne t'en fait pas, les logarithmes sont assez difficiles à comprendre au début!
Premièrement, la constante e = 2,718 281 828 est la base des logarithmes naturels. Elle se nomme le nombre d'Euler. Au lieu d'écrire $$log_e$$, on écrit ln.
Ainsi, e représente simplement un nombre qui ne change jamais, c'est-à-dire une constante.
Le logarithme en base e est appelé logarithme naturel ou logarithme népérien.
Pour ce qui est de ton numéro, ce que ton enseignant veut, c'est que tu utilises les différentes propriétés des logarithmes pour trouver la réponse finale.
Si l'argument du logarithme est une multiplication de 2 facteurs, on obtient alors l'addition de 2 expressions logarithmiques.
Si l'argument du logarithme est une division de 2 termes, on obtient alors une soustraction de 2 expressions logarithmiques.
Lorsque l'argument d'un logarithme est une puissance, l’exposant peut être transformé en coefficient du même logarithme.
Le calcul du logarithme d'un argument est équivalent au quotient du logarithme de ce même argument et du logarithme de sa base, à condition que les bases soient identiques.
Je t'invite à consulter cette fiche contenant les différentes propriétés des logarithmes :
En manipulant ton expression, tu devrais être capable de la simplifier et de trouver le résultat sans avoir recours à ta calculatrice :)
Si jamais tu as d'autres questions, n'hésite surtout pas!
Mélodie 🎶
Re: Question
Note que pour ta deuxième question on veut surtout savoir si l'égalité est vraie ou fausse; ce que tu peux démontrer comme R2D2Turbo l'indique en utilisant les propriétés des logarithmes.
Pour se simplifier le travail, on multiplie l'expression de part et d'autre du signe égale par (log_2 (3) + log_2 (2)) ce qui donne
log_2 (4) + log_2 (9) = 2(log_2 (3) + log_2 (2))
log_2 (4) + log_2 (9) = 2log_2 (3) + 2log_2 (2)
or log_2 (4) = log_2 (2²) = = 2log_2 (2)
et log_2 (9) = log_2 (3²) = = 2log_2 (3)
de par le logarithme d'une puissance,
l'égalité devient donc
2log_2 (2) + 2log_2 (3) = 2log_2 (3) + 2log_2 (2)
deux sommes qui sont égales, l'énoncé est donc vrai
Re: Question
Il faut d'abord effectuer les opérations comme la multiplication d'une parenthèse
3/4(2x - 5/3) = 3/4 · 2x - 3/4 · 5/3 = 3x/2 - 5/4
puis tu regroupes les termes semblables (les termes en x et les constantes)
finalement tu isoles le x
Re: Question
Bonjour GalaxieGamma9729,
Je ne suis pas certaine de bien comprendre ta question, alors n'hésite pas à nous réécrire si je n'y réponds pas ! :)
George Brown est appelé l'un des Pères de la Confédération, car il était présent à la Conférence de Québec de 1864 durant laquelle on a rédigé un documents comprenant 72 résolutions et qui a par la suite servit de base à la rédaction de la constitution de la fédération canadienne en 1867.
Pour l'histoire complète, je t'invite à lire ce qui suit ! :) ...
La double majorité
Dès le début des années 1850, l'instabilité ministérielle s'installe au Canada-Uni pour plusieurs raisons, dont le principe de double majorité.
Sous l'Acte d'Union de 1840, la chambre d'assemblée du gouvernement est composée d'autant de députés du Haut-Canada que du Bas-Canada (42 députés chacun pour un total de 84 députés). Afin d'être élus majoritaires et ne plus voir leurs projets bloqués par l'opposition, les partis doivent obtenir la double majorité (la majorité des sièges au Haut et au Bas-Canada).
Comme les partis élus sont presque toujours minoritaires à la chambre d'assemblée, ils sont constamment contestés par le parti en opposition. Cela mène au démantèlement du gouvernement en place. Cette situation se reproduit à maintes reprises, créant une grande instabilité ministérielle.
La représentation proportionnelle ou représentation par la population (Rep by pop)
Vers 1851, la population anglophone du Haut-Canada dépasse la population francophone du Bas-Canada. Il devient alors intéressant pour les anglophones de demander ce que les francophones ont toujours voulu mais n'ont jamais obtenu avant : la représentation proportionnelle (Rep by pop), c'est-à-dire obtenir un nombre de députés à la Chambre d'assemblée en fonction du poids démographique de la population (du Haut et du Bas-Canada). C'est d'ailleurs ce que le parti politique de George Brown (Clear Grits du Haut-Canada) demande. Le but de Brown est alors de limiter le pouvoir du Bas-Canada et des francophones à la Chambre d'assemblée afin de cesser l'instabilité ministérielle. Le Rep by pop est cependant refusé par la métropole.
La Grande coalition
Face à cette instabilité ministérielle et au refus du Rep by pop par la couronne britannique, des premières négociations d'une union politique débute en juin 1864 au Canada-Uni. George Brown (Haut-Canada) propose alors de s’associer avec son opposant politique, John A. Macdonald (Haut-Canada), et avec George-Étienne Cartier (Bas-Canada). Cette association, nommée la Grande Coalition, leur permet de former d’un gouvernement majoritaire, mettant fin à l'instabilité ministérielle au Canada-Uni. Pour poursuivre leur visée d'union, les membres de la Grande Coalition ont ensuite lancé l’idée de former une union politique, économique et militaire avec les autres colonies d’Amérique du Nord. Cette union politique au sein d’une fédération permettrait non seulement de former un important ensemble économique (contrant ainsi les besoins économiques créés par la fin du Traité de réciprocité avec les États-Unis en 1864), mais aussi une meilleure défense face aux États-Unis (alors en pleine Guerre de Sécession).
La Conférence de Charlottetown
Tout comme les politiciens du Canada-Uni, les provinces maritimes envisagent elles aussi de s’unir entre elles. Afin d’en discuter, des représentants du Nouveau-Brunswick, de l’Île-du-Prince-Édouard et de la Nouvelle-Écosse se réunissent à Charlottetown du 1er au 9 septembre 1864. Quelques délégués du Canada-Uni, dont les membres de la Grande Coalition (Brown, Cartier et Macdonald) réussissent à s'y faire inviter afin de les inciter à s'unir au Canada-Uni, notamment via la construction d'un chemin de fer intercolonial qui profiterait économiquement à tous. C'est suite à cette conférence que les délégués des provinces maritimes et du Canada-Uni s’entendent sur le projet d’une union fédérale des colonies (une fédération). Afin de discuter des détails de la fédération, ils décident de se rencontrer à nouveau, à Québec, le mois suivant.
La Conférence de Québec
Durant cette conférence, on s'entend sur le tracé du chemin de fer qui relira chacune des provinces de la fédération et George Brown gagne sa cause alors qu'on décide d'utiliser la représentation proportionnelle (Rep by pop).
Un document intitulé « Résolutions de Québec » ou « 72 résolutions » résume les points importants discutés lors de la conférence et officialise l’entente entre les colonies concernant le projet de fédération. De document sert de base à la rédaction de la constitution de la fédération canadienne en 1867.
Les 33 délégués présents à la conférence de Québec (dont George Brown) seront surnommés les « Pères de la Confédération ».
Fait cocasse : Une confédération est un regroupement ou une association d'États souverains. Une confédération est donc régie par des traités internationaux qui régulent l'ensemble de ses États membres. C'est comme si chaque province du Canada était un pays en soi (le Canada n'est donc pas une confédération). Pour sa part, une fédération est un État dans lequel le pouvoir est partagé entre l'État fédéral et les États fédérés (les provinces). Ça revient à dire que l'État fédéral a la souveraineté dans ses champs de compétence (exemple : le Canada et la défense nationale) et que les provinces ont une souveraineté dans leurs champs de compétences (exemple : le Québec et l'éducation). En d'autres termes, une fédération est une union entre plusieurs États ou provinces et pour laquelle un gouvernement central est formé afin de prendre des décisions pour l'ensemble du territoire. Toutefois, chaque province garde aussi son propre gouvernement qui possède ses propres pouvoirs. Le Canada étant une fédération, les « Pères de la Confédération » devraient plutôt être nommés « Les Pères de la Fédération » ! :)
- Noémie
Re: Question
Bonjour GeaiLibre364,
Merci pour ta question!
Un mécanisme à vis sans fin et à roue dentée (engrenage) correspond simplement à une vis sans fin connectée directement à un engrenage. Le mouvement de rotation de la vis sans fin, grâce aux filets de la vis qui poussent sur les dents de l'engrenage, le fait tourner. Il s'agit donc d'un mécanisme de transmission du mouvement.
Voici une fiche pour plus d'informations :
J'espère t'avoir aidé. N'hésite pas si tu as d'autres questions!
Zachary T. :)
Re: Question
Salut!
Merci de faire appel à nos services! 🙂
C'est normal d'avoir de la difficulté à s'adapter lorsqu'il y a un grand changement dans notre vie, ne t'inquiète pas! :)
Voici quelques trucs qui pourraient te permettre d'améliorer tes résultats :
- Prendre le temps de revoir les notions apprises dans la journée lorsque tu fais tes devoirs le soir;
- Soit actif en classe. Participer aux discussions peut faciliter la rétention d'informations;
- Si tu comprends moins bien certaines notions, n'hésite pas à poser des questions à ton enseignant.e;
- Utilise ton agenda afin de bien organiser ton temps. Cela te permettra de suivre les devoirs à remettre ou de planifier ton étude en vue d'un examen.
De plus, voici quelques ressources qui pourront t'être utiles :
- Trucs pour mieux étudier : On te propose dans cet article les meilleures astuces pour mieux étudier, idéal pour commencer à mettre de l’ordre dans tes études!
- L’écriture d’une feuille de notes : Pour certains examens, comme en français ou en maths, tu peux te préparer d’avance et amener une feuille de notes. On te donne des trucs pour t’y retrouver rapidement le jour de l’examen!
- Apprendre à gérer son stress : Parfois, ce n’est pas la matière le problème, c’est plutôt le stress qui nous brouille les idées. Pour t’aider à surmonter cela, on a plein d’idées pour toi!
- Comprendre sa capacité de concentration : Il y a plusieurs façons d’améliorer ta concentration, il suffit de trouver celle qui te convient le mieux. Découvre-la!
- La mémoire, ta meilleure amie : On a bien souvent besoin d’elle lors des examens! Tu peux l’entrainer pour qu’elle t’aide au maximum lors de ta prochaine évaluation!
- Répertoire de révision : Tu peux consulter nos répertoires de révision de mathématiques, de français, d'histoire et de sciences ici! Ce super outil te présente toutes les notions étudiées en secondaire 1 dans la matière choisie, ce qui est super pratique lorsque tu révises pour un examen!
J'espère que cela t'aide! N'hésite pas à nous réécrire si tu as d'autres questions! :)
Re: Question
Bonjour KiwiSociable4529,
Merci d'utiliser la zone d'entraide,
Quand on arrive au secondaire, il est normal que les notes baissent un peu parce que le rythme est plus rapide et la matière plus difficile. Pour améliorer ses résultats, il est important d’étudier un peu chaque jour plutôt que tout faire avant un test. Par exemple, étudier entre 20 et 30 minutes par matière permet au cerveau de mieux retenir l’information grâce à la répétition.
En math, la meilleure méthode est de pratiquer régulièrement. Il faut refaire les exercices faits en classe et essayer d’en faire quelques nouveaux. Il est aussi très important de comprendre les étapes plutôt que seulement mémoriser les formules. Se poser des questions comme « pourquoi je fais cette étape » ou « d’où vient cette formule » aide beaucoup. Quand on fait une erreur, il faut la regarder et comprendre pourquoi elle est arrivée pour éviter de la refaire. Expliquer un exercice à voix haute ou à quelqu’un est aussi une très bonne méthode pour vérifier si on comprend bien.
En français, lire un peu chaque jour aide énormément. Lire entre 10 et 15 minutes améliore le vocabulaire, l’écriture et la compréhension. Faire des fiches avec les règles de grammaire, les figures de style et les types de textes est aussi très utile. Écrire souvent, même des petits résumés ou expliquer une leçon avec ses propres mots, permet de mieux retenir la matière. Apprendre du nouveau vocabulaire en notant les mots et leur signification peut aussi améliorer les résultats.
Une bonne méthode d’étude est la technique Pomodoro, qui consiste à étudier pendant 25 minutes, puis prendre une pause de 5 minutes, et répéter plusieurs fois. Finalement, il faut éviter certaines erreurs comme seulement relire les notes, étudier seulement avant les examens, ne pas poser de questions en classe ou penser qu’on est mauvais dans une matière. Avec de la pratique et une bonne méthode d’étude, il est possible d’améliorer ses notes progressivement.
Ne lâche pas, bonne étude, bon travail, bon succès et n'hésite pas à revenir nous voir si tu as d'autres questions!
LefraniResponsable4446