The Volume of Truncated Solids

A truncated solid is a solid that has been cut by a plane, and only a portion remains. The plane can be parallel or not parallel to the base.

A contractor insulates the roof of a house using polyurethane foam applied with a spray gun. Once the foam has hardened, it will look like a truncated rectangular-based pyramid.

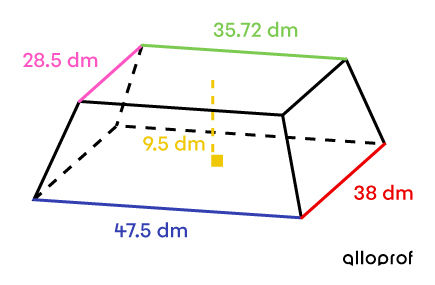
If the product costs |$4\ | for |9\ \text{dm}^3,| how much will it cost to insulate the roof?

1. Identify the solids
   It is a truncated rectangular-based pyramid. To make the calculations easier, find the initial truncated pyramid and determine its dimensions as follows:

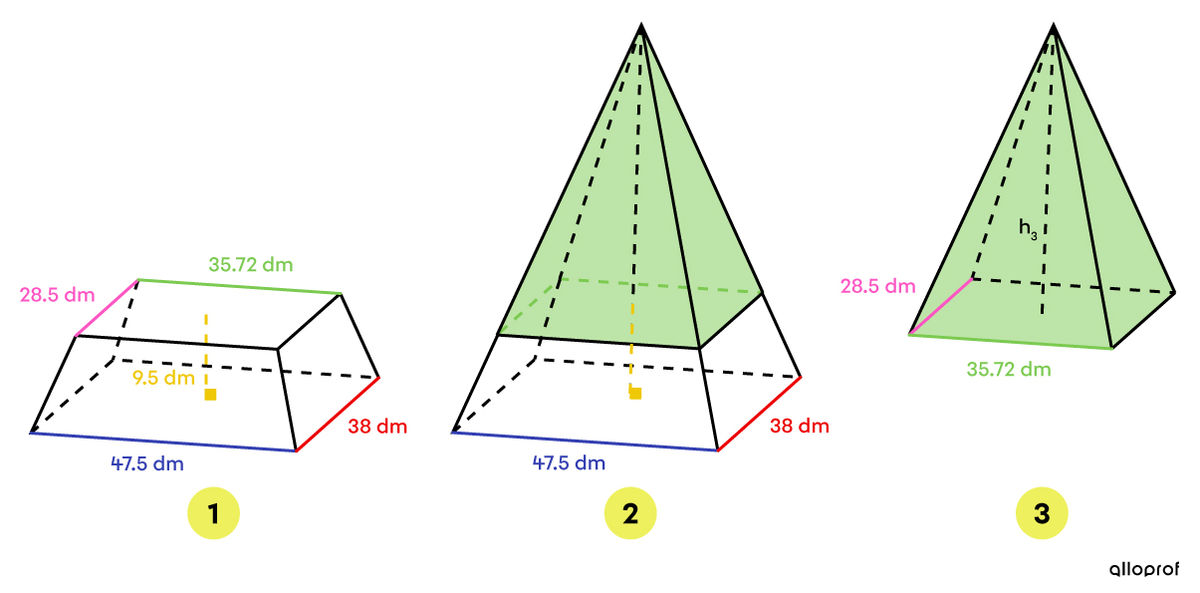
In a truncated pyramid, like in a truncated cone, the corresponding measurements are proportional. ||\dfrac{\text{Length}_2}{\text{Length}_3} = \dfrac{\text{Width}_2}{\text{Width}_3} = \dfrac{\text{Height}_2}{\text{Height}_3}||In order to calculate the height of the removed pyramid (pyramid 3), the proportion must be solved first.||\begin{align} \dfrac{\color{#EC0000}{\text{Width}_2}}{\color{#FF55C3}{\text{Width}_3}} &= \dfrac{\text{Height}_2}{\text{Height}_3} \\\\ \dfrac{\color{#EC0000}{38}}{\color{#FF55C3}{28{.}5}} &= \dfrac{h_3+\color{#EFC807}{9{.}5}}{h_3} \\\\ 38h_3 &= 28{.}5(h_3+9{.}5) \\ 38h_3 &= 28{.}5h_3 + 270{.}75 \\ 9{.}5h_3 &= 270{.}75 \\ h_3 &= 28{.}5\ \text{dm} \end{align}||Next, determine the height of the full pyramid (pyramid 2).||\begin{align} h_2 &= h_3 +\color{#EFC807}{9{.}5} \\ &= 28{.}5 + \color{#EFC807}{9{.}5} \\ &= 38 \ \text{dm} \end{align}||

2. Calculate the volume
   The volume of the roof (image 1) is obtained by subtracting the volume of pyramids 2 and 3.||\begin{align} V_{1} &= V_{2} - V_{3}\\ &= \dfrac{A_{\text{base}_2}\times h_2}{3} - \dfrac{A_{\text{base}_{3}}\times h_3}{3} \\ &= \dfrac{(47{.}5 \times 38) \times 38}{3} - \dfrac{(35{.}72 \times 28{,}5)\times 28{.}5}{3} \\ &= \dfrac{1 \ 805 \times 38}{3} - \frac{1 \ 018{.}02 \times 28{.}5}{3} \\ &\approx 22\ 863{.}33 - 9 \ 671{.}19 \\ &\approx 13 \ 192{.}14 \ \text{dm}^3 \end{align}||

3. Interpret the answer
   Create a proportion and solve it using cross-multiplication. ||\begin{align}\dfrac{$4\ }{?} &= \dfrac{9 \ \text{dm}^3}{13 \ 192{.}14\ \text{dm}^3} \\\\? &= \dfrac{4 \times 13 \ 192{.}14}{9} \\? &\approx $5 \ 863{.}17\ \end{align}|| ​​Therefore, the cost of the insulation product is approximately |$5\ 863{.}17.\\|

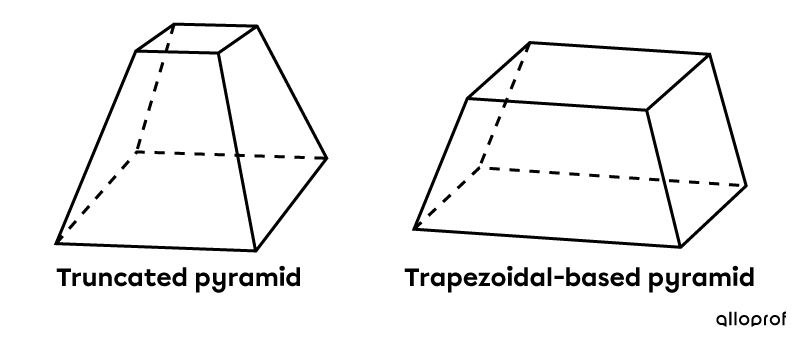
Be careful not to confuse truncated pyramids with trapezoidal-based prisms. The lateral faces of truncated pyramids are trapezoids inclined towards the interior of the solids, whereas the lateral faces of trapezoidal-based prisms are rectangles and the bases are congruent trapezoids.

A horticulturist plants tomato seeds in pots shaped like inverted truncated cones to produce a bountiful vegetable harvest.

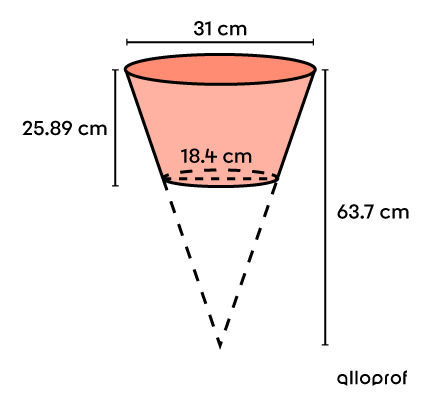
The horticulturist must have 14 plants to produce enough tomatoes. If she fills her pots to capacity, how much soil will she need to plant all the seeds?

1. Identify the solids
   It is an inverted truncated cone. Consider the initial cone to make the calculations easier.

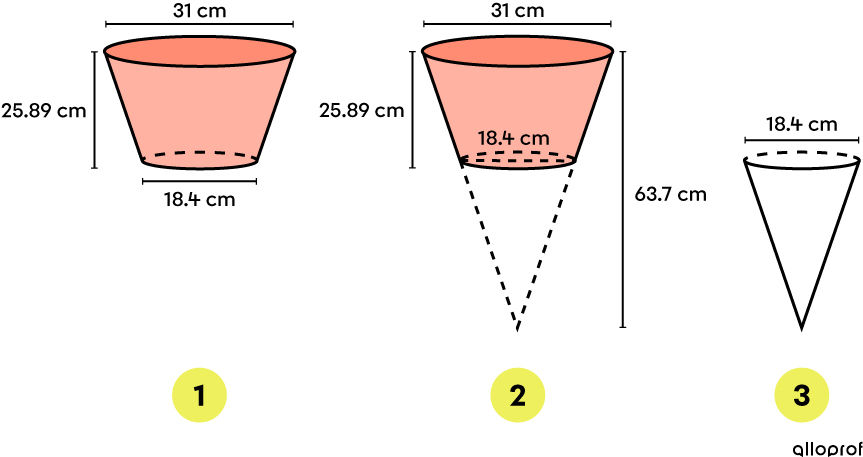
2. Calculate the volume
   Obtain the volume of the pot (image 1) by subtracting the volumes of cones 2 and 3. ||\begin{align} V_{1} &= V_{2} - V_{3}\\ &= \frac{A_{\text{base}_2}\times h_2}{3} - \frac{A_{\text{base}_{3}}\times h_3}{3}\end{align}||Since the solids are cones, each base is a circle. Thus, use the following formula:||A_{\text{base}} =\pi r^2||Next, find the radii measurements using the given diameters. ||r_2 = \dfrac{31}{2} =15{.}5\ \text{cm}\\r_3 = \dfrac{18{.}4}{2} =9{.}2\ \text{cm}||It is also necessary to calculate the height of cone 3. ||h_3 = 63{.}7 - 25{.}89 = 37{.}81\ \text{cm}|| ||\begin{align} V_{1} &= V_{2} - V_{3}\\ &= \dfrac{A_{\text{base}_2}\times h_2}{3} - \dfrac{A_{\text{base}_{3}}\times h_3}{3} \\ &= \dfrac{(\pi \times 15{.}5^2) \times 63{.}7}{3} - \dfrac{(\pi \times 9{.}2^2)\times 37{.}81}{3} \\ &= \dfrac{240{.}25\pi \times 63{.}7}{3} - \dfrac{84{.}64\pi \times 37{.}81}{3} \\ &\approx 16\ 026{.}23 - 3 \ 351{.}28 \\ &\approx 12\ 674{.}95 \ \text{cm}^3 \end{align}||

3. Interpret the answer
   The answer above is the volume of soil required for 1 pot. Since there are 14 pots to fill, perform this calculation: ||​14\ \text{pots} \times 12 \ 674{.}95\ \text{cm}^3/\text{pot}=177 \ 449{.}3 \ \text{cm}^3|| Thus, the amount of soil needed is approximately |177 \ 449{.}3\ \text{cm}^3.|