Matières
Niveaux
Les formules de périmètre, d’aire et de volume
Fiche | Mathématiques
Il existe plusieurs formules qui permettent de calculer le périmètre et l’aire de figures planes ainsi que l’aire et le volume de solides. Chacune de ces formules peut être utilisée pour trouver une mesure manquante dans une figure ou une mesure manquante dans un solide.
Les formules pour les figures planes
-
Le périmètre, généralement noté |P,| est la longueur du contour d’une figure. Dans le cas d’un cercle, le contour se nomme la « circonférence » et se note |C.|
-
L’aire, généralement notée |A,| est la surface délimitée par le contour d’une figure.
|
Figure plane |
Périmètre |
Aire |
|---|---|---|
 |
||P=\color{#3A9A38}{\boldsymbol{a}}+\color{#3B87CD}{\boldsymbol{b}}+\color{#FF55C3}{\boldsymbol{c}}|| |
||A=\dfrac{\color{#3B87CD}{\boldsymbol{b}}\times\color{#EC0000}{\boldsymbol{h}}}{2}|| |
 |
||\begin{align}P&=\color{#3A9A38}{\boldsymbol{c}}+\color{#3A9A38}{\boldsymbol{c}}+\color{#3A9A38}{\boldsymbol{c}}+\color{#3A9A38}{\boldsymbol{c}}\\&=4\color{#3A9A38}{\boldsymbol{c}}\end{align}|| |
||\begin{align}A&=\color{#3A9A38}{\boldsymbol{c}}\times\color{#3A9A38}{\boldsymbol{c}}\\&=\color{#3A9A38}{\boldsymbol{c}}^2\end{align}|| |
 |
||\begin{align}P&=\color{#3B87CD}{\boldsymbol{b}}+\color{#3B87CD}{\boldsymbol{b}}+\color{#EC0000}{\boldsymbol{h}}+\color{#EC0000}{\boldsymbol{h}}\\&=2\color{#3B87CD}{\boldsymbol{b}}+2\color{#EC0000}{\boldsymbol{h}}\\&=2(\color{#3B87CD}{\boldsymbol{b}}+\color{#EC0000}{\boldsymbol{h}})\end{align}|| |
||A=\color{#3B87CD}{\boldsymbol{b}}\times\color{#EC0000}{\boldsymbol{h}}|| |
 |
||\begin{align}P&=\color{#FF55C3}{\boldsymbol{a}}+\color{#FF55C3}{\boldsymbol{a}}+\color{#3B87CD}{\boldsymbol{b}}+\color{#3B87CD}{\boldsymbol{b}}\\&=2\color{#FF55C3}{\boldsymbol{a}}+2\color{#3B87CD}{\boldsymbol{b}}\\&=2(\color{#FF55C3}{\boldsymbol{a}}+\color{#3B87CD}{\boldsymbol{b}})\end{align}|| |
||A=\color{#3B87CD}{\boldsymbol{b}}\times\color{#EC0000}{\boldsymbol{h}}|| |
 |
||\begin{align}P&=\color{#3A9A38}{\boldsymbol{c}}+\color{#3A9A38}{\boldsymbol{c}}+\color{#3A9A38}{\boldsymbol{c}}+\color{#3A9A38}{\boldsymbol{c}}\\&=4\color{#3A9A38}{\boldsymbol{c}}\end{align}|| |
||A=\dfrac{\color{#FF55C3}{\boldsymbol{D}}\times\color{#3B87CD}{\boldsymbol{d}}}{2}|| |
 |
||P=\color{#3B87CD}{\boldsymbol{b}}+\color{#3A9A38}{\boldsymbol{a}}+\color{#FA7921}{\boldsymbol{B}}+\color{#FF55C3}{\boldsymbol{c}}|| |
||A=\dfrac{(\color{#3B87CD}{\boldsymbol{b}}+\color{#FA7921}{\boldsymbol{B}})\times\color{#EC0000}{\boldsymbol{h}}}{2}|| |
 |
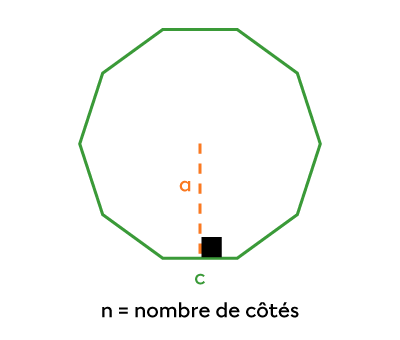||P=n\times\color{#3A9A38}{\boldsymbol{c}}|| |
||A=\dfrac{\color{#3A9A38}{\boldsymbol{c}}\color{#FA7921}{\boldsymbol{a}}n}{2}|| |
 |
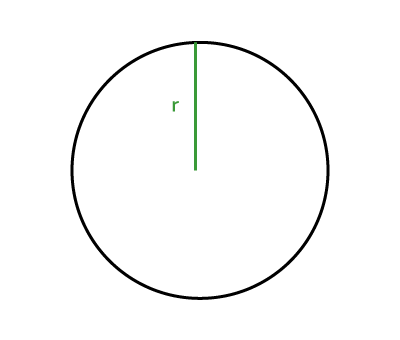||C=2\pi\color{#3A9A38}{\boldsymbol{r}}|| |
||A=\pi\color{#3A9A38}{\boldsymbol{r}}^2|| |
Les formules pour les solides
-
L'aire de la base, généralement notée |A_b,| est la surface occupée par la ou les figures servant de base à un solide.
-
L'aire latérale, généralement notée |A_L,| est la surface occupée par les figures ne servant pas de bases à un solide.
-
L'aire totale, généralement notée |A_T,| est la surface occupée par toutes les figures formant un solide.
-
Le volume, généralement noté |V,| est l’espace délimité par les faces d’un solide.
|
Solide |
Formules d'aire |
Formule de volume |
|---|---|---|
|
Cube  |
L'aire des cubes||\begin{align}A_b&=\color{#3a9a38}{\boldsymbol{c}}^2\\\\ A_L&=4\color{#3a9a38}{\boldsymbol{c}}^2\\\\A_T&=6\color{#3a9a38}{\boldsymbol{c}}^2\end{align}|| |
Le volume des cubes||V=\color{#3a9a38}{\boldsymbol{c}}^3|| |
|
Prisme  |
L'aire des prismes||\begin{align}\color{#3b87cd}{\boldsymbol{A_b}}&=\text{formule appropriée}\\\\A_L&=P_b\times\color{#ec0000}{\boldsymbol{h}}\\\\A_T&=A_L+2\color{#3b87cd}{\boldsymbol{A_b}}\end{align}|| |
Le volume des prismes||V=\color{#3b87cd}{\boldsymbol{A_b}}\times\color{#ec0000}{\boldsymbol{h}}|| |
|
Pyramide  |
L'aire des pyramides||\begin{align}\color{#3b87cd}{\boldsymbol{A_b}}&=\text{formule appropriée}\\\\A_L&=\dfrac{P_b\times\color{#fa7921}{\boldsymbol{a}}}{2}\\\\A_T&=A_L+\color{#3b87cd}{\boldsymbol{A_b}}\end{align}|| |
Le volume des pyramides||V=\dfrac{\color{#3b87cd}{\boldsymbol{A_b}}\times\color{#ec0000}{\boldsymbol{h}}}{3}|| |
|
Sphère ou boule  |
L'aire des sphères||A_T=4\pi\color{#3a9a38}{\boldsymbol{r}}^2|| |
Le volume des boules||V=\dfrac{4\pi\color{#3a9a38}{\boldsymbol{r}}^3}{3}|| |
|
Cylindre  |
L'aire des cylindres||\begin{align}\color{#3b87cd}{\boldsymbol{A_b}}&=\pi\color{#3a9a38}{\boldsymbol{r}}^2\\\\A_L&=2\pi\color{#3a9a38}{\boldsymbol{r}}\color{#ec0000}{\boldsymbol{h}}\\\\A_T&=A_L+2\color{#3b87cd}{\boldsymbol{A_b}}\end{align}|| |
Le volume des cylindres||V=\color{#3b87cd}{\boldsymbol{A_b}}\times\color{#ec0000}{\boldsymbol{h}}|| |
|
Cône  |
L'aire des cônes||\begin{align}\color{#3b87cd}{\boldsymbol{A_b}}&=\pi\color{#3a9a38}{\boldsymbol{r}}^2\\\\A_L&=\pi\color{#3a9a38}{\boldsymbol{r}}\color{#fa7921}{\boldsymbol{a}}\\\\A_T&=A_L+\color{#3b87cd}{\boldsymbol{A_b}}\end{align}|| |
Le volume des cônes||V=\dfrac{\color{#3b87cd}{\boldsymbol{A_b}}\times\color{#ec0000}{\boldsymbol{h}}}{3}|| |