Subjects
Grades
Formulas for Perimeter, Area and Volume
Concept sheet | Mathematics
There are several formulas that can be used to calculate the perimeter and area of plane figures, as well as the area and volume of solids. Each of these formulas can be used to find a missing measurement in a figure or a missing measurement in a solid.
Table of contents
Formulas for Plane Figures
-
The perimeter, generally denoted |P,| is the length of the contour of a figure. In the case of the circle, the perimeter is called “circumference” and is denoted |C.|
-
The area, generally denoted |A,| is the surface delimited by a figure.
|
Plane Figure |
Perimeter |
Area |
|---|---|---|
 |
||P=\color{#3A9A38}{\boldsymbol{a}}+\color{#3B87CD}{\boldsymbol{b}}+\color{#FF55C3}{\boldsymbol{c}}|| |
||A=\dfrac{\color{#3B87CD}{\boldsymbol{b}}\times\color{#EC0000}{\boldsymbol{h}}}{2}|| |
 |
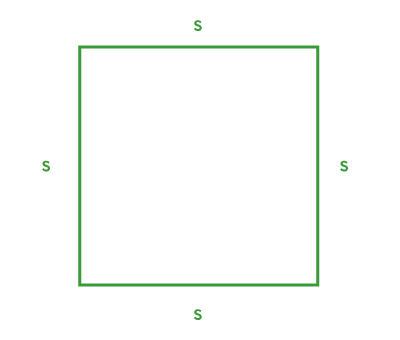||\begin{align}P&=\color{#3A9A38}{\boldsymbol{s}}+\color{#3A9A38}{\boldsymbol{s}}+\color{#3A9A38}{\boldsymbol{s}}+\color{#3A9A38}{\boldsymbol{s}}\\&=4\color{#3A9A38}{\boldsymbol{s}}\end{align}|| |
||\begin{align}A&=\color{#3A9A38}{\boldsymbol{s}}\times\color{#3A9A38}{\boldsymbol{s}}\\&=\color{#3A9A38}{\boldsymbol{s}}^2\end{align}|| |
 |
||\begin{align}P&=\color{#3B87CD}{\boldsymbol{b}}+\color{#3B87CD}{\boldsymbol{b}}+\color{#EC0000}{\boldsymbol{h}}+\color{#EC0000}{\boldsymbol{h}}\\&=2\color{#3B87CD}{\boldsymbol{b}}+2\color{#EC0000}{\boldsymbol{h}}\\&=2(\color{#3B87CD}{\boldsymbol{b}}+\color{#EC0000}{\boldsymbol{h}})\end{align}|| |
||A=\color{#3B87CD}{\boldsymbol{b}}\times\color{#EC0000}{\boldsymbol{h}}|| |
 |
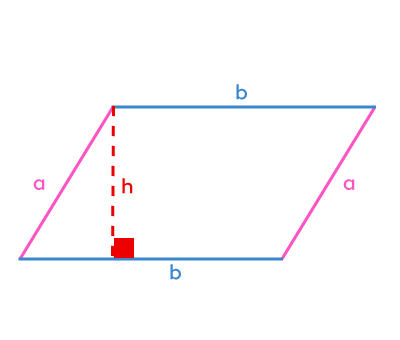||\begin{align}P&=\color{#FF55C3}{\boldsymbol{a}}+\color{#FF55C3}{\boldsymbol{a}}+\color{#3B87CD}{\boldsymbol{b}}+\color{#3B87CD}{\boldsymbol{b}}\\&=2\color{#FF55C3}{\boldsymbol{a}}+2\color{#3B87CD}{\boldsymbol{b}}\\&=2(\color{#FF55C3}{\boldsymbol{a}}+\color{#3B87CD}{\boldsymbol{b}})\end{align}|| |
||A=\color{#3B87CD}{\boldsymbol{b}}\times\color{#EC0000}{\boldsymbol{h}}|| |
 |
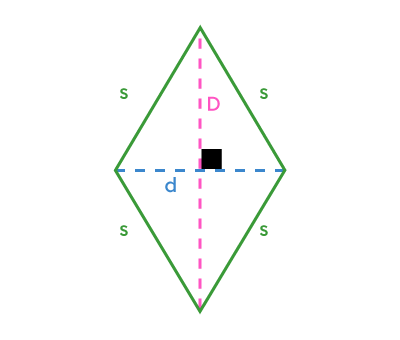||\begin{align}P&=\color{#3A9A38}{\boldsymbol{s}}+\color{#3A9A38}{\boldsymbol{s}}+\color{#3A9A38}{\boldsymbol{s}}+\color{#3A9A38}{\boldsymbol{s}}\\&=4\color{#3A9A38}{\boldsymbol{s}}\end{align}|| |
||A=\dfrac{\color{#FF55C3}{\boldsymbol{D}}\times\color{#3B87CD}{\boldsymbol{d}}}{2}|| |
 |
||P=\color{#3B87CD}{\boldsymbol{b}}+\color{#3A9A38}{\boldsymbol{a}}+\color{#FA7921}{\boldsymbol{B}}+\color{#FF55C3}{\boldsymbol{c}}|| |
||A=\dfrac{(\color{#3B87CD}{\boldsymbol{b}}+\color{#FA7921}{\boldsymbol{B}})\times\color{#EC0000}{\boldsymbol{h}}}{2}|| |
 |
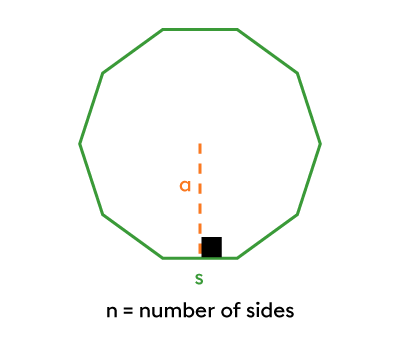||P=n\times\color{#3A9A38}{\boldsymbol{s}}|| |
||A=\dfrac{\color{#3A9A38}{\boldsymbol{s}}\color{#FA7921}{\boldsymbol{a}}n}{2}|| |
 |
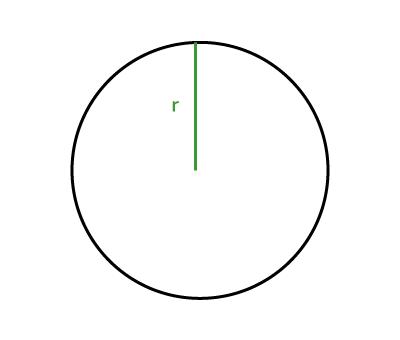||C=2\pi\color{#3A9A38}{\boldsymbol{r}}|| |
||A=\pi\color{#3A9A38}{\boldsymbol{r}}^2|| |
Formulas for Solids
-
The area of the base, generally denoted |A_b,| is the surface occupied by the figure(s) that serve as base for a solid.
-
The lateral area, generally denoted |A_L,| is the surface occupied by the figures that do not serve as base for a solid.
-
The total area, generally denoted |A_T,| is the surface occupied by all the figures forming a solid.
-
The volume, generally denoted |V,| is the space delimited by the faces of a solid.
|
Solid |
Area Formula |
Volume Formula |
|---|---|---|
|
Cube  |
Area of Cubes||\begin{align}A_b&=\color{#3a9a38}{\boldsymbol{s}}^2\\\\ A_L&=4\color{#3a9a38}{\boldsymbol{s}}^2\\\\A_T&=6\color{#3a9a38}{\boldsymbol{s}}^2\end{align}|| |
Volume of Cubes||V=\color{#3a9a38}{\boldsymbol{s}}^3|| |
|
Prism  |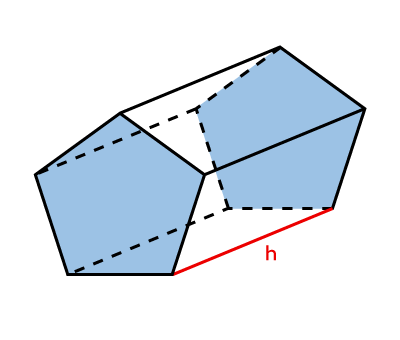
Area of Prisms||\begin{align}\color{#3b87cd}{\boldsymbol{A_b}}&=\text{relevant formula}\\\\A_L&=P_b\times\color{#ec0000}{\boldsymbol{h}}\\\\A_T&=A_L+2\color{#3b87cd}{\boldsymbol{A_b}}\end{align}|| |
Volume of Prisms||V=\color{#3b87cd}{\boldsymbol{A_b}}\times\color{#ec0000}{\boldsymbol{h}}|| |
|
Pyramid  |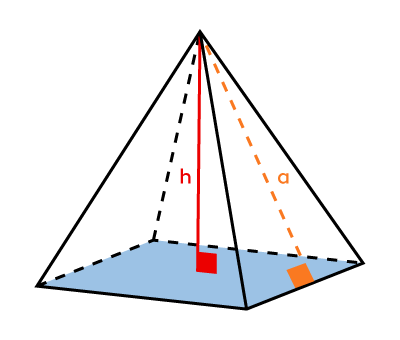
Area of Pyramids||\begin{align}\color{#3b87cd}{\boldsymbol{A_b}}&=\text{relevant formula}\\\\A_L&=\dfrac{P_b\times\color{#fa7921}{\boldsymbol{a}}}{2}\\\\A_T&=A_L+\color{#3b87cd}{\boldsymbol{A_b}}\end{align}|| |
Volume of Pyramids||V=\dfrac{\color{#3b87cd}{\boldsymbol{A_b}}\times\color{#ec0000}{\boldsymbol{h}}}{3}|| |
|
Sphere  |
Area of Spheres||A_T=4\pi\color{#3a9a38}{\boldsymbol{r}}^2|| |
Volume of Spheres||V=\dfrac{4\pi\color{#3a9a38}{\boldsymbol{r}}^3}{3}|| |
|
Cylinder  |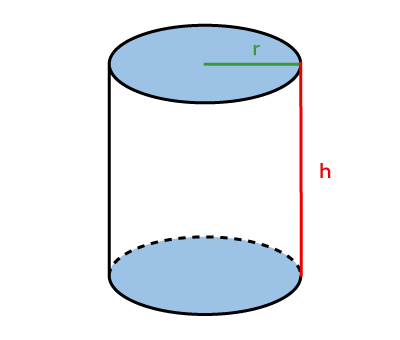
Area of Cylinders||\begin{align}\color{#3b87cd}{\boldsymbol{A_b}}&=\pi\color{#3a9a38}{\boldsymbol{r}}^2\\\\A_L&=2\pi\color{#3a9a38}{\boldsymbol{r}}\color{#ec0000}{\boldsymbol{h}}\\\\A_T&=A_L+2\color{#3b87cd}{\boldsymbol{A_b}}\end{align}|| |
Volume of Cylinders||V=\color{#3b87cd}{\boldsymbol{A_b}}\times\color{#ec0000}{\boldsymbol{h}}|| |
|
Cone  |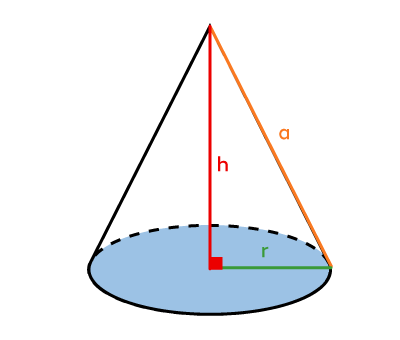
Area of Cones||\begin{align}\color{#3b87cd}{\boldsymbol{A_b}}&=\pi\color{#3a9a38}{\boldsymbol{r}}^2\\\\A_L&=\pi\color{#3a9a38}{\boldsymbol{r}}\color{#fa7921}{\boldsymbol{a}}\\\\A_T&=A_L+\color{#3b87cd}{\boldsymbol{A_b}}\end{align}|| |
Volume of Cones||V=\dfrac{\color{#3b87cd}{\boldsymbol{A_b}}\times\color{#ec0000}{\boldsymbol{h}}}{3}|| |