Matières
Niveaux
Les solides équivalents
Fiche | Mathématiques
Secondaire
4-5
Table des matières
Des solides équivalents sont des solides qui ont le même volume.
Des solides isométriques sont nécessairement des solides équivalents et de même aire totale.
Cependant, des solides équivalents ou de même aire ne sont pas nécessairement des solides isométriques. En effet, 2 solides équivalents peuvent être complètement différents.
On peut démontrer que la pyramide et le cube suivants sont équivalents en calculant leur volume respectif.
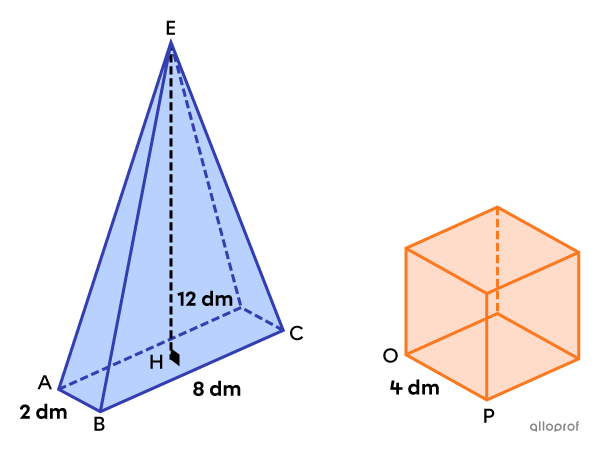
||\begin{align}V_\text{pyramide}&=\dfrac{\text{m}\overline{AB}\times\text{m}\overline{BC}\times\text{m}\overline{EH}}{3}\\&=\dfrac{2\times8\times12}{3}\\&=64\ \text{dm}^3\end{align}||
||\begin{align}V_\text{cube}&=\left(\text{m}\overline{OP}\right)^3\\&=4^3\\&=64\ \text{dm}^3\end{align}||
Conclusion : La pyramide et le cube sont équivalents, puisqu’ils ont chacun un volume de |64\ \text{dm}^3.|
La recherche de mesures manquantes dans des solides équivalents
Il est souvent nécessaire d'utiliser l'algèbre pour trouver des mesures manquantes dans des solides équivalents. Voici la démarche à suivre pour y arriver.
-
Déterminer l’équation formée par l’équivalence entre le volume des solides.
-
Résoudre l’équation.
-
Répondre à la question.
Voici un 1er exemple dans lequel il n’y a qu’une seule inconnue.
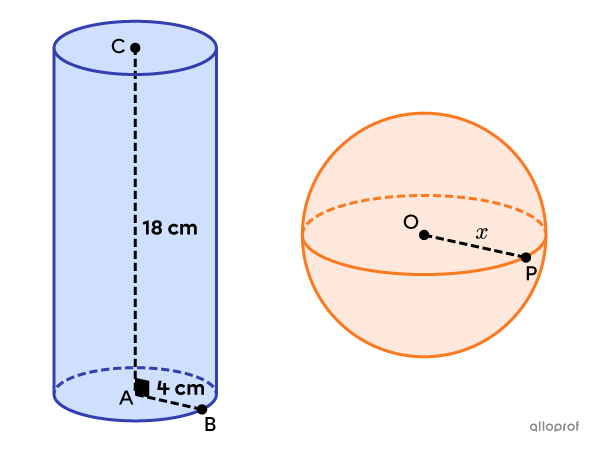
Trouve le rayon de la boule, sachant qu’elle est un solide équivalent au cylindre.
Voir la solution
Voici un 2e exemple dans lequel il y a plusieurs inconnues.
Trouve la hauteur de la pyramide, sachant qu’elle est un solide équivalent au cône.
Voir la solution
La comparaison de l’aire totale de solides équivalents
Il est possible de dégager certaines conjectures concernant l’aire totale de solides équivalents. On examine plusieurs exemples pour vérifier que chacune de ces propositions est vraie.
La plus petite aire totale parmi les prismes à base rectangulaire équivalents
Parmi tous les prismes à base rectangulaire équivalents, c'est le cube qui possède la plus petite aire totale.
Cette conjecture est similaire à celle qui concerne le plus petit périmètre parmi les figures équivalentes à |n| côtés, mais elle s'applique en particulier aux prismes droits à 6 faces.
De plus, cette conjecture est l’inverse de celle qui concerne le plus grand volume parmi les prismes de même aire.
Soit les prismes à base rectangulaire et le cube suivants.
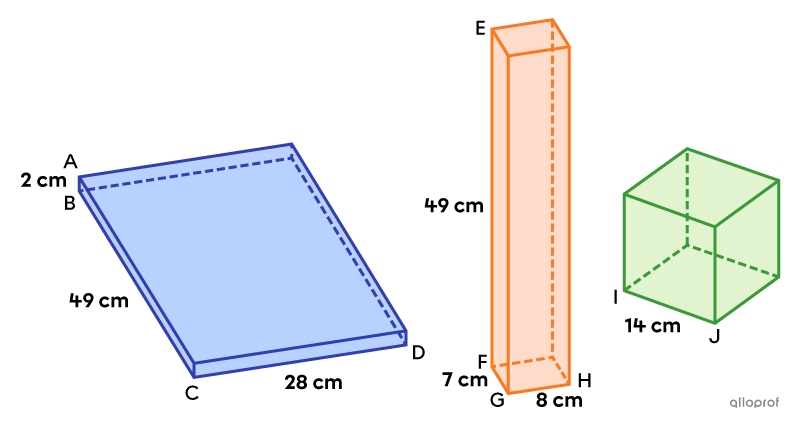
Ces 3 prismes sont équivalents, puisqu’ils ont tous un volume de |2\ 744\ \text{cm}^3.|
Volume du prisme bleu
||\begin{align}V_\text{prisme bleu}&=\text{m}\overline{BC}\times\text{m}\overline{CD}\times\text{m}\overline{AB}\\&=49\times28\times2\\&=2\ 744\ \text{cm}^3\end{align}||
Volume du prisme orange
||\begin{align}V_\text{prisme orange}&=\text{m}\overline{FG}\times\text{m}\overline{GH}\times\text{m}\overline{EF}\\&=7\times8\times49\\&=2\ 744\ \text{cm}^3\end{align}||
||\begin{align}V_\text{cube}&=\left(\text{m}\overline{IJ}\right)^3\\&=14^3\\&=2\ 744\ \text{cm}^3\end{align}||
Toutefois, chaque aire totale est différente.
Aire totale du prisme bleu
||\begin{align}A_\text{base}&=\text{m}\overline{BC}\times\text{m}\overline{CD}\\&=49\times28\\&=1\ 372\ \text{cm}^2\\\\A_\text{latérale}&=\left(2\times\text{m}\overline{BC}+2\times\text{m}\overline{CD}\right)\times\text{m}\overline{AB}\\&=(2\times49+2\times28)\times2\\&=308\ \text{cm}^2\\\\A_\text{prisme bleu}&=2A_\text{base}+A_\text{latérale}\\&=2\times1\ 372+308\\&=3\ 052\ \text{cm}^2\end{align}||
Aire totale du prisme orange
||\begin{align}A_\text{base}&=\text{m}\overline{FG}\times\text{m}\overline{GH}\\&=7\times8\\&=56\ \text{cm}^2\\\\A_\text{latérale}&=\left(2\times\text{m}\overline{FG}+2\times\text{m}\overline{GH}\right)\times\text{m}\overline{EF}\\&=(2\times7+2\times8)\times49\\&=1\ 470\ \text{cm}^2\\\\A_\text{prisme orange}&=2A_\text{base}+A_\text{latérale}\\&=2\times56+1\ 470\\&=1\ 582\ \text{cm}^2\end{align}||
||\begin{align}A_\text{cube}&=6\left(\text{m}\overline{IJ}\right)^2\\&=6\times14^2\\&=1\ 176\ \text{cm}^2\end{align}||
Ainsi, parmi ces 3 prismes à base rectangulaire équivalents, c'est le cube qui possède la plus petite aire totale.
La plus petite aire totale parmi les solides équivalents
Parmi tous les solides équivalents, c'est la boule qui possède la plus petite aire totale.
Cette conjecture est similaire à celle qui concerne le plus petit périmètre parmi les figures équivalentes.
De plus, cette conjecture est l’inverse de celle qui concerne le plus grand volume parmi les solides de même aire.
Soit le cube, l’octaèdre régulier et la boule qui suivent.
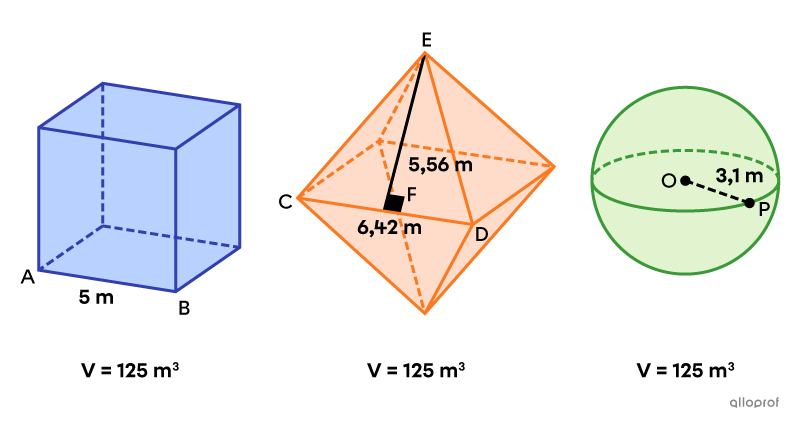
Ces 3 solides sont équivalents, puisqu’ils ont tous un volume de |125\ \text{m}^3.| Toutefois, chaque aire totale est différente.
||\begin{align}A_\text{cube}&=6\left(\text{m}\overline{AB}\right)^2\\&=6\times5^2\\&=150\ \text{m}^2\end{align}||
Aire totale de l’octaèdre régulier
Toutes les faces d’un octaèdre régulier sont des triangles équilatéraux. Puisqu’il y a 8 faces, on calcule l’aire totale de l’octaèdre de la façon suivante.||\begin{align}A_\text{octaèdre}&=8\left(\dfrac{\text{m}\overline{CD}\times\text{m}\overline{EF}}{2}\right)\\&=4\times6{,}42\times5{,}56\\&\approx142{,}78\ \text{m}^2\end{align}||
||\begin{align}A_\text{boule}&=4\pi\left(\text{m}\overline{OP}\right)^2\\&=4\pi(3{,}1)^2\\&\approx120{,}76\ \text{m}^2\end{align}||
Ainsi, parmi ces 3 solides équivalents, c'est la boule qui possède la plus petite aire totale.
À voir aussi
- La similitude, l'isométrie et l'équivalence
- Les figures isométriques et semblables
- Les solides isométriques et semblables
- Les rapports de similitude, d'aires et de volumes (k, k², k³)
- Les conditions minimales d'isométrie des triangles
- Les conditions minimales de similitude des triangles
- Le théorème de Thalès
- Les figures équivalentes
- Les solides de même aire