Matières
Niveaux
Voici un petit guide de préparation contenant toutes les notions abordées en quatrième secondaire dans la séquence CST. Pour expliquer le tout, chaque formule sera suivie d'un exemple et d'un lien qui mène à une fiche de notre bibliothèque virtuelle.
||y = ax + b||où ||a = \dfrac{\Delta y}{\Delta x} = \dfrac{y_2 - y_1}{x_2 - x_1}||
Avec les informations qui sont fournies dans le graphique ci-dessous, détermine l'équation de la droite sous sa forme fonctionnelle.
||y = ax^2||où la valeur de |a| est déterminée par substitution d'un point.
Avec les informations qui sont fournies dans le graphique ci-dessous, détermine l'équation de la parabole.
Pour la fonction polynomiale de degré 2, |a \ne \dfrac{\Delta y}{\Delta x}.|
||y = a(c)^x||où
|a:| Valeur initiale
|c:| Base (facteur multiplicatif)
En 2005, la population des crapauds d'un étang s'élevait à 500. Pour différentes raisons, la population diminue de 5 % chaque année. Si le rythme se maintient, en quelle année y aura-t-il environ 368 crapauds?
Dans un tel graphique, les points pleins (|\bullet|) représentent des données qui sont incluses alors que les points vides (|\circ|) représentent des données qui ne sont pas incluses.
Lors de l'ouverture du Centre Vidéotron à Québec, tous les Québécois ont eu l'opportunité de se procurer des billets afin d'aller le visiter. En théorie, la visite était d'une durée de deux heures, mais les gens avaient la possibilité de quitter l'édifice après une heure de visite. Ainsi, on peut modéliser cette situation selon le graphique suivant :
Selon le graphique ci-dessus, combien y avait-il de Québécois dans le Centre Vidéotron à 18 h?
Dans une fonction périodique, un cycle fait référence au motif qui se répète alors que la période est la durée du cycle selon l'axe des |x.|
De retour de vacance, Marie-Claude décide de se remettre en forme en faisant du vélo avec son groupe d'amies. Pour guider le groupe, un entraineur fait le trajet avec eux et c'est lui qui décide de la vitesse à maintenir. Afin de préparer le groupe à la prochaine séance, l'entraineur remet ce graphique à chacun des membres du groupe :
En sachant que l'entrainement consiste à répéter le même trajet pendant 45 minutes, Marie-Claude se demande pendant combien de minutes, au total, elle aura pédalé à une vitesse minimale de 16 km/h?
Pour l'étude d'une fonction, ce sont toujours les mêmes propriétés qu'il faut analyser :
le domaine : toutes les valeurs possibles de |x|
le codomaine (l'image) : toutes les valeurs possibles de |y|
les abscisses à l'origine : la valeur du |x| quand |y=0|
l'ordonnée à l'origine : la valeur du |y| quand |x=0|
maximum : la plus grande valeur de |y|
minimum : la plus petite valeur de |y|
croissance : quand le graphique ne « descend » pas
décroissance : quand le graphique ne « monte » pas
Le signe :
positive : portion du graphique qui est au-dessus ou égale à l'axe des |x|
négative : portion du graphique qui est en-dessous ou égale à l'axe des |x|
En tant que comptable d'une grande compagnie, tu dois donner un compte rendu détaillé de l'évolution des profits au cours de la dernière année. Pour t'aider, voici le graphique des 12 derniers mois.
Avant de préparer ton discours de présentation et afin de bien alimenter ton argumentation, tu dois faire l'étude complète du graphique.
Pour résoudre un système d'équations par comparaison, on peut se fier aux étapes suivantes :
Identifier les variables reliées aux inconnus.
Créer les équations selon la mise en situation.
Isoler la même variable pour chacune des équations.
Comparer les deux équations pour en former une nouvelle.
Résoudre cette nouvelle équation.
Remplacer la valeur de la variable dans une des équations de départ pour trouver la valeur de l'autre variable.
Au dépanneur du coin, un groupe de travailleurs achètent 4 cafés et 6 muffins pour |15{,}06\ $.| Le lendemain, ce même groupe se procure 3 cafés et 5 muffins pour une somme de |11{,}97\ $.| Si, le jour d'après, ces travailleurs veulent se procurer 6 cafés et 4 muffins, quelle somme devra être déboursée?
Pour résoudre une système d'équations par substitution, on peut se fier aux étapes suivantes :
Identifier les variables reliées aux inconnus.
Créer les équations selon la mise en situation.
Isoler une variable dans une des deux équations.
Substituer cette même variable dans l'autre équation par l'expression algébrique qui lui est associée.
Résoudre cette nouvelle équation.
Remplacer la valeur de la variable dans une des équations de départ pour trouver la valeur de l'autre variable.
Au dépanneur du coin, un groupe de travailleurs achètent 4 cafés et 6 muffins pour |15{,}06\ $.| Le lendemain, ce même groupe se procure 3 cafés et 5 muffins pour une somme de |11{,}97\ $.| Si, le jour d'après, ces travailleurs veulent se procurer 6 cafés et 4 muffins, quelle somme devra être déboursée?
Pour résoutre un système d'équation par réduction, on peut se fier aux étapes suivantes :
Identifier les variables reliées aux inconnus.
Créer les équations selon la mise en situation.
Trouver des équations équivalentes pour obtenir le même coefficient d'une même variable.
Soustraire les deux équations.
Isoler la variable restante pour trouver sa valeur.
Remplacer la valeur de la variable dans une des équations de départ pour trouver la valeur de l'autre variable.
Au dépanneur du coin, un groupe de travailleurs achètent 4 cafés et 6 muffins pour |15{,}06\ $.| Le lendemain, ce même groupe se procure 3 cafés et 5 muffins pour une somme de |11{,}97\ $.| Si, le jour d'après, ces travailleurs veulent se procurer 6 cafés et 4 muffins, quelle somme devra être déboursée?
Selon le triangle rectangle qui suit, on peut en déduire 3 théorèmes.
Dans un triangle rectangle, la mesure de chaque côté de l’angle droit est moyenne proportionnelle entre la mesure de sa projection sur l’hypoténuse et celle de l’hypoténuse entière.||\begin{align} \dfrac{m}{a} = \dfrac{a}{c}\ &\Leftrightarrow\ a^2 = m c \\\\ \dfrac{n}{b} = \dfrac{b}{c}\ &\Leftrightarrow\ b^2 = n c \end{align}||
Dans un triangle rectangle, la mesure de la hauteur issue du sommet de l’angle droit est moyenne proportionnelle entre les mesures des deux segments qu’elle détermine sur l’hypoténuse. ||\dfrac{m}{h} = \dfrac{h}{n}\ \Leftrightarrow\ h^2 = m n||
Dans le triangle rectangle, le produit des mesures de l’hypoténuse et de la hauteur correspondante égale le produit des mesures des côtés de l’angle droit. ||c h = a b||
Afin de se distinguer des autres entrepreneurs, une compagnie de construction suggère des maisons avec des toits de différentes formes. Parmi ces choix, on a la forme suivante :
Afin d'estimer les couts de production, l'entrepreneur a besoin des deux mesures extérieures manquantes de ce triangle |(\overline {AB}, \overline {BC}).| Aide-le à les déterminer.
En considérant l'angle |\theta| comme référence, on a :
|\sin \theta = \dfrac{\text{Mesure du côté opposé à }\ \theta}{\text{Mesure de l'hypoténuse}}|
|\cos \theta = \dfrac{\text{Mesure du côté adjacent à }\ \theta}{\text{Mesure de l'hypoténuse}}|
|\tan \theta = \dfrac{\text{Mesure du côté opposé à} \ \theta}{\text{Mesure du côté adjacent à} \ \theta}|
Afin de s'assurer de respecter les normes du bâtiment, l'angle d'élévation des fermes de toit d'une maison doit être d'un minimum de |25^\circ.| Pour s'assurer de respecter cette contrainte, un fabriquant décide d'établir cet angle à |35^\circ.| Si on sait que la longueur de la ferme de toit est de 13 mètres, quelles seront les mesures des deux autres côtés de cette pièce de bois?
Afin de déterminer le trajet à suivre par un hélicoptère pour aller chercher des gens en détresse en forêt, on a triangulé la carte de la région avec l'emplacement actuel de l'hélicoptère, l'hôpital et les gens qui sont en détresse.
Selon ce dessin, quelle orientation devrait suivre l'hélicoptère pour se rendre le plus rapidement possible aux gens en détresse?
Selon le triangle quelconque qui suit, on peut en déduire une série d'équivalences.
|\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C}|
Lors de certaines festivités westerns, des courses de chevaux sont organisées pour animer le spectacle. Lors de ces courses, les cowboys doivent faire le tour de chacun des trois barils qui sont disposés en forme de triangle isocèle.
À l'aide des mesures données, quelle est la distance entre chacun des barils?
Afin d'assurer un aérodynamisme maximal, le profil de certains voitures de course ressemble à un triangle.
Afin que ces proportions soient conservées, quelle devrait être la mesure de l'angle qui se situe près de la roue arrière?
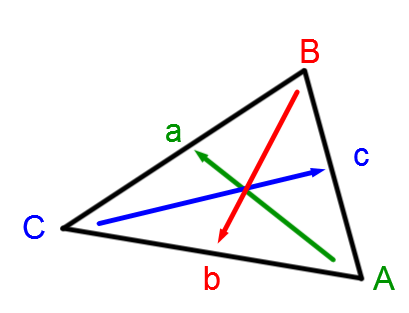
Quand on identifie le triangle, il est toujours essentiel de mettre
|\color{green}{\text{le côté a opposé à l'angle A}}|
|\color{red}{\text{le côté b opposé à l'angle B}}|
|\color{blue}{\text{le côté c opposé à l'angle C}}|
Selon le triangle quelconque qui suit, on peut calculer son aire en utilisant la formule ci-dessous.
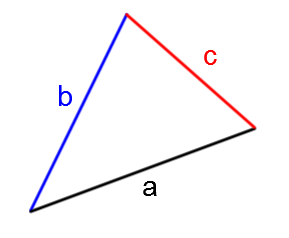
|\text{Aire}=\sqrt{p(p - a)(p - \color{blue}{b})(p - \color{red}{c})}|
où
|p=\dfrac{a + \color{blue}{b} + \color{red}{c}}{2}|
Afin de s'assurer d'un bon rapport qualité-prix, une banque veut calculer la surface du plancher couverte par le champ de vision d'une caméra de surveillance.
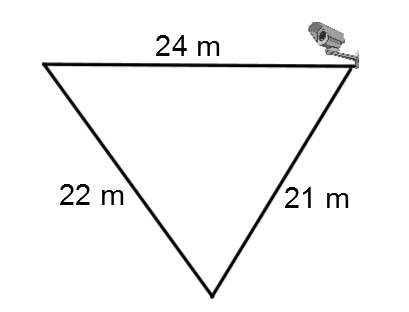
À l'aide des informations ci-dessus, détermine la superficie de cette région.
A - C - A : Deux triangles sont isométriques quand une paire de côtés homologues isométriques est incluse entre deux paires d'angles homologues isométriques.
C - A - C : Deux triangles sont isométriques quand une paire d'angles homologues isométriques est incluse entre deux paires de côtés homologues isométriques.
C - C - C : Deux triangles sont isométriques quand chacune des paires de côtés homologues sont isométriques.
Dû à des problèmes de machinerie, les employés d'une compagnie de construction doivent monter eux-mêmes les fermes de toit de forme triangulaire afin de terminer la construction d'une maison. Or, ils doivent s'assurer qu'elles soient toutes identiques.
Avec les informations fournies ci-dessus, démontre que ces deux constructions sont isométriques.
A - A : Deux triangles sont semblables quand deux paires d'angles homologues sont isométriques.
C - A - C : Deux triangles sont semblables quand une paire d'angles homologues isométriques est incluse entre deux paires de côtés homologues proportionnels.
C - C - C : Deux triangles sont semblables si les trois paires de côtés homologues sont proportionnels.
Dans le cadre d'une levée de fonds pour un organisme communautaire, la ville organise une course à pied à faire en famille. Par ailleurs, ils tiennent à ce que le trajet fait par les adultes soit semblable à celui des enfants.
En tenant compte des informations données ci-dessus, démontre que les deux trajets sont semblables.
|\text{Distance} = \sqrt{(y_2 - y_1)^2 + (x_2 - x_1)^2}|
où
|(x_1, y_1):| Coordonnées du point situé au début du segment
|(x_2, y_2):| Coordonnées du point situé à l'autre extrémité du segment
Afin de déterminer la quantité d'essence qu'un avion doit avoir dans son réservoir pour faire un vol Montréal-Paris, on représente chacune de ces deux villes sur un plan cartésien gradué en kilomètre.
Quelle est la distance, en kilomètres, entre ces deux villes?
Soit |(x,y),| les coordonnées du point de partage recherchée. ||x=x_1+ \dfrac{a}{b} (x_2-x_1)|| ||y=y_1+ \dfrac{a}{b} (y_2-y_1)||
où
|(x_1,y_1):| Coordonnées du début du segment
|(x_2,y_2):| Coordonnées de fin du segment
|\dfrac{a}{b}:| Fraction qui définit le partage du segment
À chaque matin, tu dois te rendre à l'arrêt d'autobus pour attendre ton moyen de transport qui te reconduit à ton école. Afin que l'arrêt soit centralisé pour les autres élèves du coin, tu as remarqué qu'il partageait le segment de rue qui rejoint ta maison à ton école dans un rapport |1 : 4.|
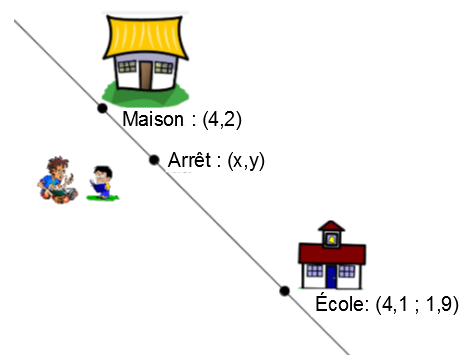
En utilisant les informations disponibles, détermine la coordonnée de l'endroit où se situe ton arrêt d'autobus.
Il est important de bien différencier les deux types de notations utilisées pour illustrer la portion associée à un point de partage pour ensuite utiliser la notation appropriée à la formule : ||\begin{matrix}\text{Rapport} \\ \Large{a:b} \end{matrix} \Leftrightarrow\ \begin{matrix}\text{Fraction} \\ \large\frac{a}{a+b} \end{matrix}||
Les droites |y_1 = a_1 x + b_1| et |y_2 = a_2 x + b_2| sont parallèles si et seulement si |a_1 = a_2.|
Quelle est l'équation de la droite qui est parallèle à celle identifiée dans le plan cartésien ci-dessous et qui passe par le point C?
Les droites |y_1 = a_1 x + b_1| et |y_2 = a_2 x + b_2| sont perpendiculaires si et seulement si |a_1 \times a_2 = -1.|
On dit aussi que deux droites sont perpendiculaires si la pente de l'une est l'opposée de l'inverse de la pente de l'autre : |a_2 = \dfrac{-1}{a_1}.|
Quelle est l'équation de la droite qui est perpendiculaire à celle identifiée dans le plan cartésien ci-dessous et qui passe par le point C?
|EM = \dfrac{\sum \mid x_i - \overline {x} \mid}{n}|
où
|x_i| représente chacune des données
|\sum| représente la somme
|n| représente le nombre total de données
Lors du dernier mois, 11 maisons ont été vendues dans un même quartier pour les montants suivants :
|\color{blue}{156\ 700\ $},| |\color{red}{158\ 900\ $},| |159\ 000\ $,| |162\ 500\ $,| |164\ 100\ $,| |167\ 400\ $,| |172\ 000\ $,| |175\ 000\ $,| |178\ 100\ $,| |179\ 000\ $,| |183\ 000\ $.|
À des fins de statistiques pour les agents immobiliers, calcule l'écart moyen de cette distribution.
|R_{100}(x) = \displaystyle \frac{\text{nombre de données inférieures} + \frac{\text{nombre de données égales}}{2}}{\text{nombre total de données}} \times 100|
Remarque : On arrondit à l'entier supérieur si la réponse obtenue n'est pas entière.
Dans un processus pour combler un des différents postes de travail dans la fonction publique fédérale, tu dois passer une épreuve écrite. Voici la liste des résultats, en pourcentage, des différents participants :
Pour s'assurer de garder les meilleurs candidats, seulement ceux qui ont un résultat qui est supérieur au |85^e| rang centile seront retenus. À la lumière de ces informations, est-ce que ta candidature sera retenue si tu as obtenu un résultat de |84\ \%?|
|\text{Rang de la donnée} = \dfrac{\text{rang centile}}{100} \times \text{nombre total de données}|
Remarque : On arrondit à l'unité inférieure si la réponse n'est pas entière.
Dans un processus pour combler un des différents postes de travail dans la fonction publique fédérale, les candidats doivent réaliser une épreuve écrite. Voici la liste des résultats, en pourcentage, des différents participants :
Pour s'assurer de garder les meilleurs candidats, seulement ceux qui ont un résultat qui est supérieur au |82^e| rang centile seront retenus. À la lumière de ces informations, à partir de quel résultat est-ce que les candidats seront retenus?
Le nuage de points est utilisé pour estimer la corrélation qui existe entre deux variables. Pour avoir une idée plus précise de la corrélation, il faut calculer le coefficient de corrélation.
Depuis cinq ans, une nouvelle entreprise ne cesse d'augmenter ses profits et cherche à agrandir son centre de production. Par contre, elle veut s'assurer que la croissance économique de sa compagnie soit positive et fortement régulière. Pour analyser le tout, voici le recensement des revenus commerciaux des 30 dernières semaines.
À ton avis, est-ce que la croissance économique de l'entreprise est positive et fortement régulière?
Après avoir encadré le nuage de points et pris la mesure de la longueur |(L)| et la largeur |(l)| du rectangle :||r = \pm \left(1 - \dfrac{l}{L}\right)||Pour ce qui est du signe, il sera donné en fonction du sens du nuage de points.
On peut également utiliser ce coefficient pour qualifier la corrélation :
| Valeur de |r| | Force du lien linéaire |
|---|---|
| Près de |0| | Nulle |
| Près de |\pm 0{,}50| | Faible |
| Près de |\pm 0{,}75| | Moyenne |
| Près de |\pm 0{,}87| | Forte |
| Près de |\pm 1| | Très forte |
| |\pm 1| | Parfaite |
Afin de faire un bilan sur la réussite des étudiants qui s'inscrivent dans les établissements d'enseignements pour adultes, les membres de la direction s'intéressent à la corrélation entre l'absentéisme aux différents cours (en heures) et la moyenne générale (en %) à la fin de l'année scolaire. Pour bien analyser le tout, ils ont regroupé les données dans un nuage de points :
Quel est le coefficient de corrélation de cette étude?
Pour trouver l'équation de la droite de régression selon la méthode médiane-médiane, on peut se fier aux étapes suivantes :
Mettre les couples en ordre croissant selon la valeur des |x.|
Séparer les couples en trois groupes égaux, si possible.
Calculer la coordonnée médiane |(M_1, M_2, M_3)| de chacun des groupes.
Calculer la coordonnée moyenne |(P_1)| des trois points médians.
Calculer la valeur de la pente |(a)| avec |M_1| et |M_3.|
Calculer la valeur de la valeur initiale |(b)| avec |P_1.|
Écrire l'équation de la droite de régression sous la forme |y = ax + b.|
Avant de construire une nouvelle tour à condo et d'en faire l'emménagement paysager, on s'intéresse à la hauteur des arbres afin qu'ils ne cachent pas la vue aux futurs résidents pour au moins les 20 prochaines années. Pour estimer la hauteur de ces derniers, on utilise la table de valeurs suivante :
À l'aide de ces informations, détermine à quelle hauteur devrait se situer les premiers balcons afin que la vue ne soit pas obstruée par les arbres.
Même si la situation et les données sont les mêmes, il est normal que la réponse finale varie selon la méthode utilisée (Méthode médiane-médiane ou Méthode de Mayer).
Puisque ce sont des méthodes qui servent à estimer et non à prédire les résultats avec certitude, il se peut qu'il y ait une différence entre les deux résultats.
Pour trouver l'équation de la droite de régression selon la méthode de Mayer, on peut se fier aux étapes suivantes :
Mettre les couples en ordre croissant selon la valeur en |x.|
Séparer les couples en deux groupes égaux, si possible.
Calculer les points moyens |(P_1| et |P_2)| de chacun des groupes.
Utiliser ces points moyens pour trouver la valeur de la pente |(a)| et de la valeur initiale |(b).|
Écrire l'équation de la droite de régression sous la forme |y = ax + b.|
Avant de construire une nouvelle tour à condo et d'en faire l'emménagement paysager, on s'intéresse à la hauteur des arbres afin qu'ils ne cachent pas la vue aux futurs résidents pour au moins les 20 prochaines années. Pour estimer la hauteur de ces derniers, on utilise la table de valeurs suivante :
À l'aide de ces information, détermine à quelle hauteur devrait se situer les premiers balcons afin que la vue ne soit pas obstruée par les arbres.
Même si la situation et les données sont les mêmes, il est normal que la réponse finale varie selon la méthode utilisée (Méthode médiane-médiane ou Méthode de Mayer).
Puisque ce sont des méthodes qui servent à estimer et non à prédire les résultats avec certitude, il se peut qu'il y ait une différence entre les deux résultats.