Subjects
Grades
The following is a short preparation guide containing all the concepts covered in Secondary V in the TS pathway. Each formula is followed by an example and a link to a concept sheet in our virtual library.
Here are the laws and properties of exponents that will be useful for the rest of this section:
|a^{-m} = \displaystyle \frac{1}{a^m}|
|a^{\frac{m}{n}} = \sqrt[n]{a^m}|
|a^m \times a^n = a ^{m+n}|
|\displaystyle \frac{a^m}{a^n} = a^{m-n}|
|(ab)^m = a^m b^m|
|\left(\dfrac{a}{b}\right)^m = \dfrac{a^m}{b^m}|
|(a^m)^n = a^{m n}|
Simplify the following expression to the maximum.||\dfrac{(27 a^3 b)^{\frac{1}{2}}}{27^{\frac{1}{3}}a^3}||
In general, the law of the multiplication of radicals is used to factor: |\sqrt { a \times b} = \sqrt{a} \times \sqrt{b}.| Before performing the calculation, it is necessary to:
Decompose the radicand into a product of factors, one of which is a square number
Transform the root of a product into a product of roots |(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b})|
Calculate the root of the square number
What is the simplified value of the following root?
||\sqrt{45}||
Here are the rules of logarithms that are important to master:
|\log_c(M \times N) = \log_c M + \log_c N|
|\log_{c}\left(\dfrac{M}{N}\right)=\log_{c}M-\log_{c}N|
|\log_{\frac{1}{c}}M=-\log_{c}M|
|\log_c M^n = n \log_c M|
|\log_a b = \dfrac{\log_c b}{\log_c a}|
Using the laws of logarithms, simplify the following expression. ||(\log_4 3x^2 + \log_4 4y - \log_4 6x)^4||
To find the values of |x| , if they exist, use the following:
General form
|0 = ax^2 + bx + c|, with this formula: ||\{x_1, x_2\} = \dfrac{-b \pm \sqrt{b^2-4ac}}{2a}||
Standard form
|0 = a(x-h)^2+k|
where |(h,k) =| coordinates of the vertex
Isolate the |x| with the reverse order of operations.
Factored form
|0 = a(x-z_1)(x-z_2)|
where |\{z_1,z_2\}=| zeros of the function resulting in 2 equations:
|x-z_1 = 0| and |x-z_2=0.|
At the 2012 Summer Olympics, Great Britain's Greg Rutherford made the following jump.
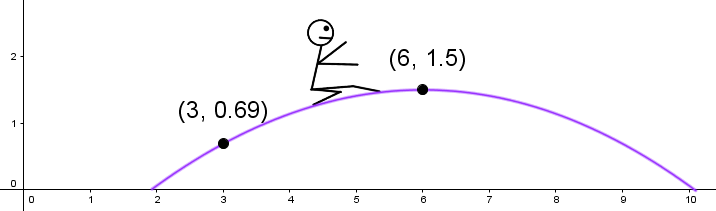
Assuming that his jump follows a parabola model, determine the distance of Greg's jump.
To solve an inequality related to this model, begin by following the same steps while adding one of these steps:
Sketch a graph of the situation
Check the inequality using a point
The solution set of an inequality is directly related to the equation associated with it.
||f(x) = a \log_c (b(x-h))||where the zero of the function |= \dfrac{1}{b} + h| and |h = | asymptote
Consider the following function.
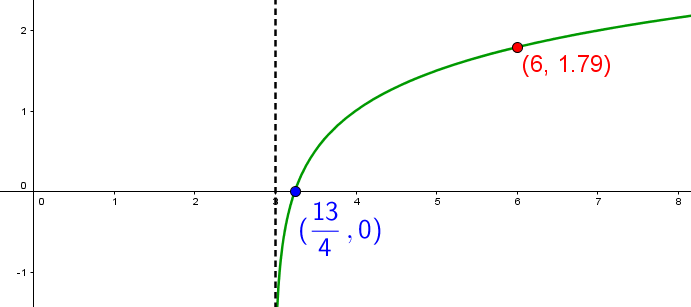
What is the value of the x-coordinate if the y-coordinate is 3?
To solve an inequality related to this model, begin by following the same steps while adding one of these steps:
Sketch a graph of the situation
Check the inequality using a point
The solution set of an inequality is directly related to the equation associated with it.
||f(x) = a c ^{bx} + k||where
|b = | compounding frequency
|k = | asymptote
|c = 1\, \pm| percentage change as a decimal number
When an investment is made in a banking institution, its return is generally evaluated according to an exponential function. However, to benefit from certain more advantageous rates, a minimum investment sum is required.
For example, after how many years does an initial investment of |$5\ 000| capitalized every |2| years at an interest rate of |5\ \%| with a minimum investment of |$3\ 000| is it at least |$8\ 000|?
To solve an inequality related to this model, begin by following the same steps while adding one of these steps:
Sketch a graph of the situation
Check the inequality using a point
The solution set of an inequality is directly related to the equation associated with it.
||f(x) = a \sqrt{b(x-h)} + k||where
|(h,k) = | coordinates of the vertex,
|b = | generally |\pm 1,|
the signs |a| and |b| depend on the orientation of the curve.
As a birdwatcher, you watch a bird take flight from a branch three metres above the ground. Its trajectory follows the following pattern.
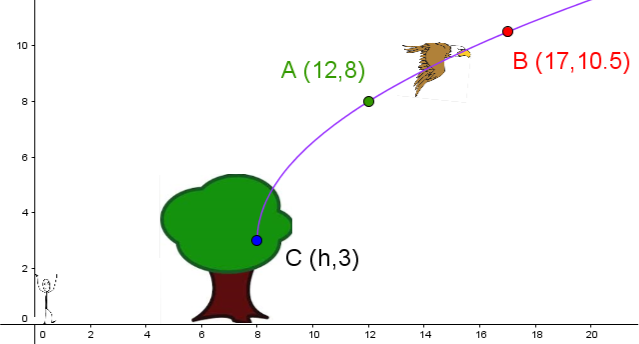
Knowing that it is still possible to observe the bird at a height of |50\ \text{m},| what will be the horizontal distance separating you from the bird at that precise moment?
To solve an inequality related to this model, begin by following the same steps while adding one of these steps:
Sketch a graph of the situation
Check the inequality using a point
The solution set of an inequality is directly related to the equation associated with it.
Standard form: |f(x) = \displaystyle \frac{a}{b(x-h)} + k|
General form: |f(x) = \displaystyle \frac{ax+b}{cx+d}|
Based on the information available in the graph, determine the x-coordinate of point |\color{red}{B}.|
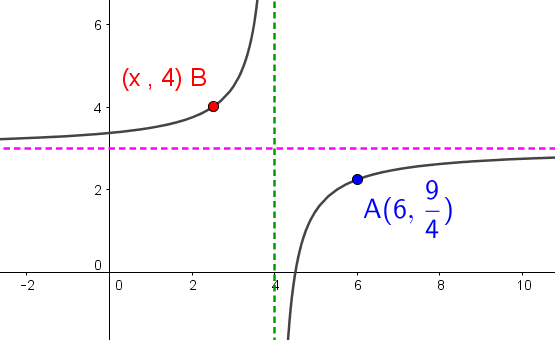
To solve an inequality related to this model, begin by following the same steps while adding one of these steps:
Sketch a graph of the situation
Check the inequality using a point
The solution set of an inequality is directly related to the equation associated with it.
The rule of a step function (greatest integer function) is written in the following form: || f(x) = a \left[ b(x-h)\right] + k||
with |(h,k) = | coordinates of an included point,
|\vert a\vert = | vertical distance between two steps, and
|\dfrac{1}{\vert b \vert} = | length of a step.
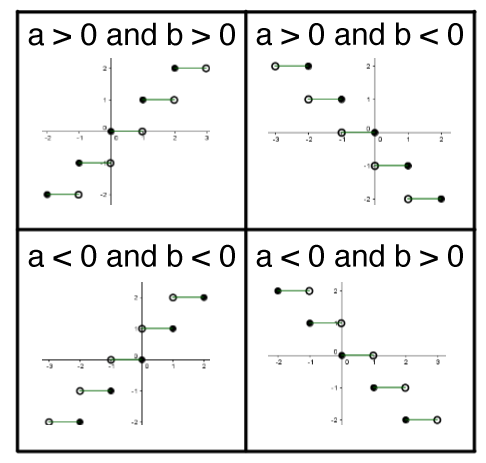
To determine the sign of |a| and of |b,| the order of the open and closed points, as well as the variation (increase or decrease) of the graph, are important.
A grocery store has a new reward program that offers stamps for discounts on certain items.
Customers receive five stamps with a minimum purchase of $5. They receive seven more stamps for every additional $22 they spend.
Using this information, what interval corresponds to a customer's total bill if they receive 47 stamps from their purchase?
To solve an inequality related to this model, begin by following the same steps while adding one of these steps:
Sketch a graph of the situation
Check the inequality using a point
The solution set of an inequality is directly related to the equation associated with it.
Depending on the situation, choose from three models of trigonometric functions:
|f(x) = a \cos (b (x-h)) + k|
|g(x) = a \sin(b (x-h)) + k|
|h(x) = a \tan(b (x-h)) + k|
To keep your dog entertained, you decide to go outside and play his favourite game of “go fetch”. You are standing 10 metres from the house. You always throw the ball 30 metres from you. In addition, you noticed that at this distance, your dog takes 12 seconds to fetch the ball and bring it back to you. Of course, you throw the ball again as soon as he brings it back to you. You do this for five minutes.
However, since your dog is not perfectly trained, you are afraid that he will run away when he is more than 30 metres from the house. Taking this information into account, for how long during the game are you afraid that your dog will run away?
To solve an inequality related to this model, begin by following the same steps while adding one of these steps:
Sketch a graph of the situation
Check the inequality using a point
The solution set of an inequality is directly related to the equation associated with it.
To perform operations on functions, we use the same concepts as the ones discussed for the simplification of algebraic expressions:
Addition and subtraction
On the coefficients of like terms
Multiplication and division
On the coefficients of all the terms while respecting the laws of exponents
Speculating on the stock market is a real passion for some investors. To try to predict the values of different stocks and the potential profits, they use different graphs and then associate them with mathematical models. To study a certain foreign company, we can use the following functions to model the different variables that influence the final return on each share:
Number of shares on the market: |f(x) = 10x - 500|
Profit from a share: |g(x) = -x^2+160x - 6\ 400|
Number of shareholders: |h(x)= -2x^2 + 260x - 8\ 000|
where |x =| number of years since its creation
What function could be used to determine the average profit obtained by each shareholder?
The composition of functions is written |g \circ f = g\big(f(x)\big).| |g \circ f| can be read as "g composite f".
To determine their budget for the following year, the Alloprof administration committee looked at the production costs of the virtual library files. They used two functions:
Function f: |t = \dfrac{5}{4} n|
Function g: |s = 124t + 2\ 000|
where |n = | number of files produced, |t=| the number of hours worked, and |s = | salary (in $) to be paid to employees.
Model this situation using a single function and then determine the total number of concept sheets that can be made with a budget of $13 625.
Generally, an optimization problem can be solved by following these steps:
Identify variables and unknowns.
Determine the equation of the function to be optimized as well as the target objective (minimize or maximize).
Create a system of inequalities.
Sketch the polygon of constraints.
Determine the coordinates of each of the polygon’s vertices.
Substitute the coordinates of each vertex in the function to be optimized to determine the optimal solution(s).
Give a complete answer taking into account the context.
To maximise his company's profits, a managing director wants to know how many jackets and shirts he has to sell each week. Because of certain production constraints, he knows that the maximum number of shirts corresponds to subtracting the quadruple of jackets from 21. Because of transport, the number of jackets must be greater than or equal to the difference between 8 and three times the number of shirts. Finally, the remainder between triple the number of jackets and double the number of shirts must be at least two.
Knowing that each jacket sold generates a profit of $32 and that the profit from the sale of a shirt is $17, what is the maximum weekly profit he can expect to make?
Two figures are equivalent when they have the same area.
To ensure that the cost of paving his new residential car park is the same as that of his old one, Julien wants his two entrances to be equivalent.
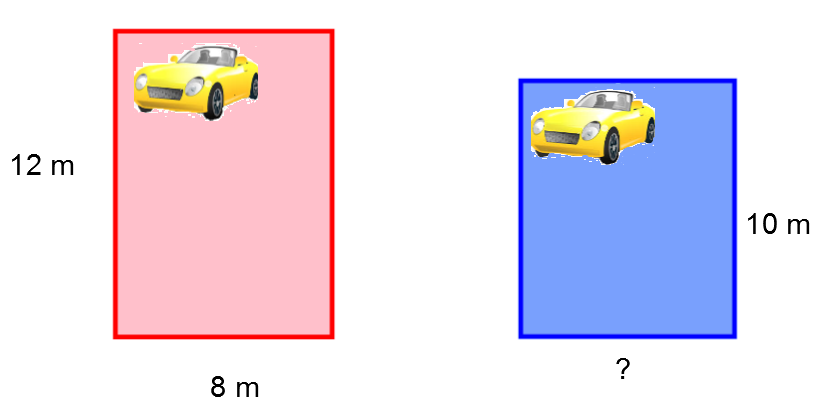
So how wide should his new parking area must be?
Two solids are equivalent when they have the same volume.
A company specialising in outdoor accessories wants to offer two different tent models. To keep production costs the same, the company wants the two models to be equivalent.
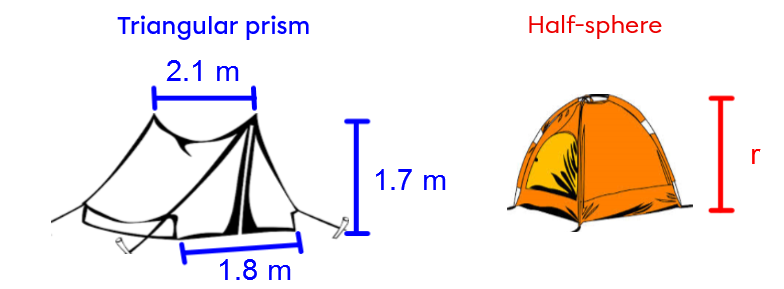
What should the height of the second model be in order to meet the similarity condition?
An angle measure of one radian corresponds to the angle at the centre formed by an arc of a circle whose measure is equivalent to the radius.
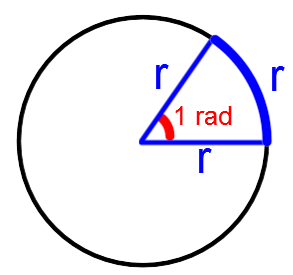
In addition, the following proportion can be used to transform a measurement in degrees into a measurement in radians and vice versa. ||\dfrac{\text{Angle measure in degrees}}{180^\circ} = \dfrac{\text{Angle measure in radians}}{\pi \text{ rad}}||
If an angle measures |\color{red}{227^\circ},| what is its measure in radians?
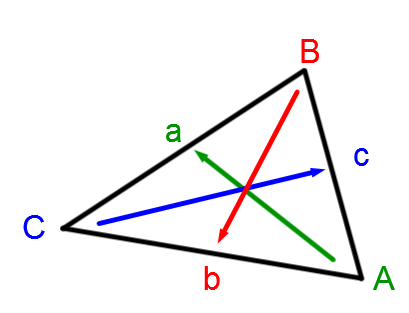
From the triangle that follows, we can deduce a series of equivalences.
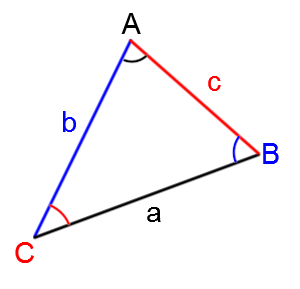
||\dfrac{a}{\sin A} = \dfrac{b}{\sin B} =\dfrac{c}{\sin C}||
At some western festivities, horse races are organised to liven up the show. During these races, the cowboys have to go around each of the three barrels, which are arranged in the shape of an isosceles triangle.
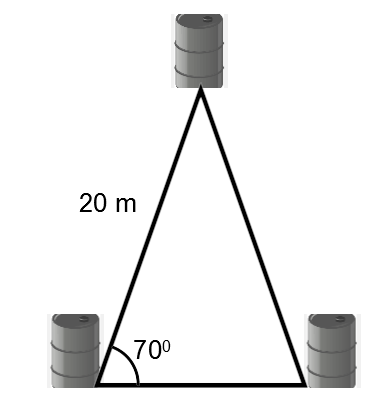
Using the data, what is the distance between each of the barrels?
To ensure maximum aerodynamics, the profile of some racing cars resembles a triangle.
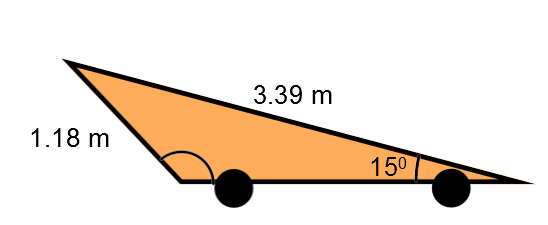
In order to maintain these proportions, what should the angle near the rear wheel be?
When identifying the triangle, it is always essential to put:
|\color{green}{\text{the side }a\text{ opposite angle }A}|
|\color{red}{\text{the side }b\text{ opposite angle }B}|
|\color{blue}{\text{the side }c\text{ opposite angle }C}|
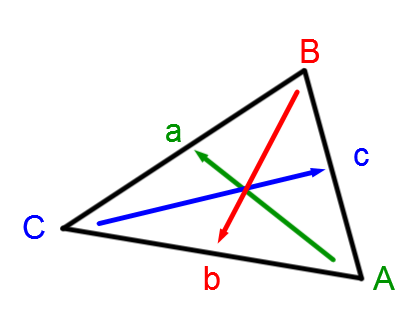
Three equivalences can be deduced from the triangle that follows.

||a^2 = \color{blue}{b}^2 + \color{red}{c}^2 - 2 \color{blue}{b} \color{red}{c} \cos A||
||\color{blue}{b}^2 = a^2 + \color{red}{c}^2 - 2 a \color{red}{c} \cos \color{blue}{B}||
||\color{red}{c}^2 = a^2 + \color{blue}{b}^2 - 2 a \color{blue}{b} \cos \color{red}{C}||
To maximise his chances for hunting a moose, a bow hunter sets up in a corner of his field and the range of his arrows is described according to the following triangle.
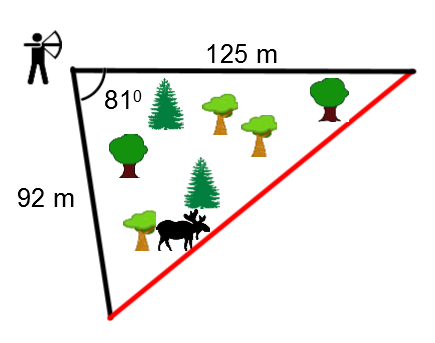
Based on the information in the drawing, how far can the moose walk, remaining as far as possible from the hunter?
To ensure the safety of its employees, a bank installs a rotating surveillance camera in the entrance hall. A security guard is also assigned to monitor this same region, which is defined by the following triangle.
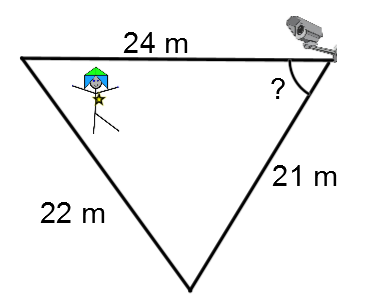
To ensure there are no blind spots, what should the camera's angle of rotation measure?
When identifying the triangle, it is always essential to put:
|\color{green}{\text{side }a\text{ opposite angle }A}|
|\color{red}{\text{side }b\text{ opposite angle }B}|
|\color{blue}{\text{side }c\text{ opposite angle }C}|
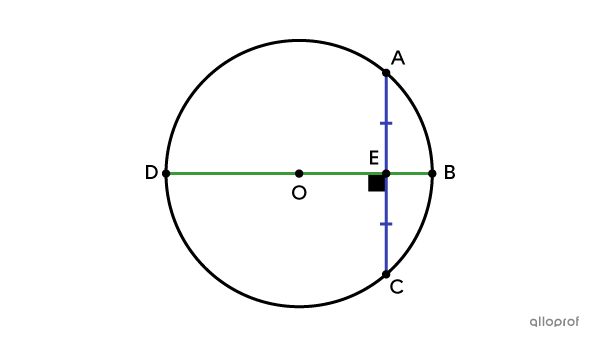
If |\color{green}{\overline{BD}} \perp \color{blue}{\overline{AC}}| and |\color{green}{\overline{BD}}| is a diameter, then |\color{blue}{\overline{AC}}| is divided into two equal parts.
If |\color{blue}{\overline{AD}}| and |\color{red}{\overline{BC}}| are an equal distance from the centre, then |\text{m} \ \color{blue}{\overline{AD}} = \text{m} \ \color{red}{\overline{BC}}.|

|\text{m} \ \color{blue}{\overline{PA}} \times \ \text{m} \ \color{blue}{\overline{PB}} = \text{m} \ \color{red}{\overline{PC}} \times \ \text{m} \ \color{red}{\overline{PD}}|
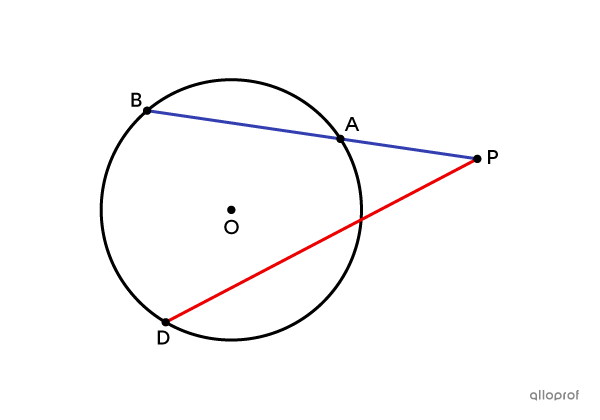
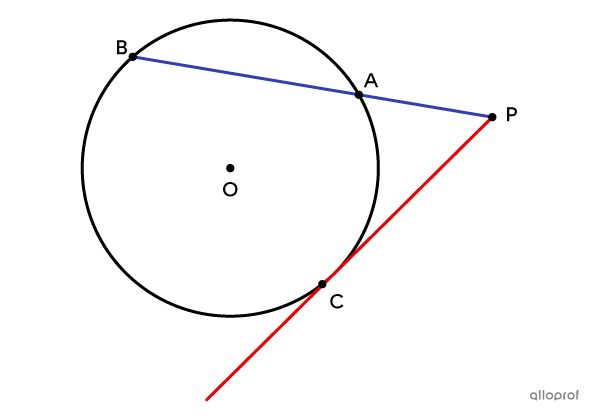
|\text{m}\ \color{blue}{\overline{PA}} \times \ \text{m} \ \color{blue}{\overline{PB}} = \text{m} \ \color{red}{\overline{PC}}^2|
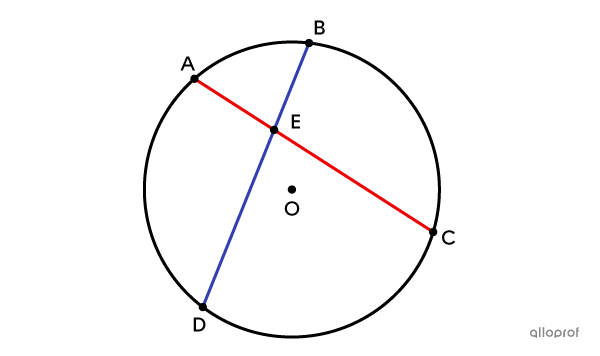
|\text{m} \ \color{red}{\overline{AE}} \times \ \text{m}\ \color{red}{\overline{CE}} = \text{m}\ \color{blue}{\overline{BE}} \times \text{m}\ \color{blue}{\overline{DE}}|
Knowing that |\overline{BF}| is a diameter, what is the measure of |\color{fuchsia}{\overline{FI}}?|

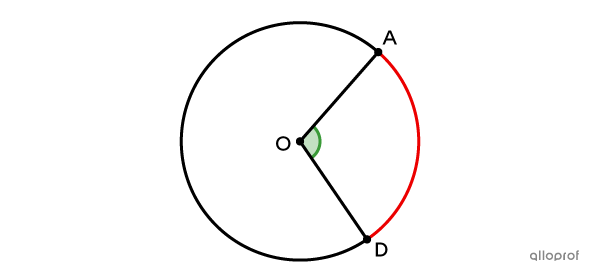
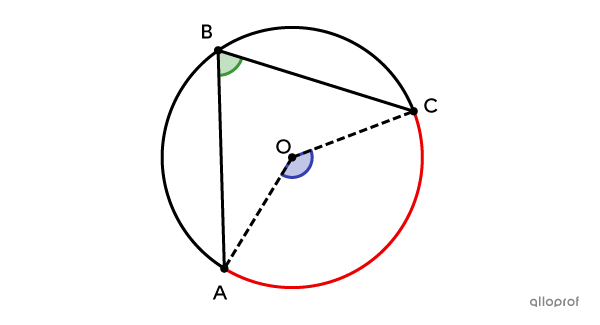
It is important to note that |\text{m} \ \overset{\ \huge\frown}{{AD}}| refers to the measurement of the angle at the centre which intercepts the arc in question.||\text{m} \ \overset{\ \huge\frown}{{\color{red}{AD}}} = \text{m} \ \color{green}{\angle AOD}||
|\begin{align}\color{green}{\text{m} \ \angle ABC} &= \dfrac{\color{blue}{\text{m}\ \angle AOC}}{2}\\\color{green}{\text{m}\ \angle ABC} &= \dfrac{\color{red}{\text{m} \overset{\ \huge\frown}{{AC}}}}{2}\end{align}|
|\begin{align}\color{green}{\text{m} \ \angle AEB} &= \dfrac{\color{red}{\text{m} \ \angle AOB} + \color{blue}{\text{m} \ \angle COD}}{2}\\
\color{green}{\text{m} \ \angle AEB} &= \dfrac {\color{red}{\text{m}\ \overset{ \huge\frown}{ {AB}}}+ \color{blue}{\text{m}\ \overset{ \huge\frown}{{CD}}}}{2}\end{align}|

|\begin{align}\color{blue}{\text{m} \ \angle AEB} &=\dfrac{\color{green}{\text{m} \ \angle AOB} - \color{red}{\text{m} \ \angle COD}}{2}\\
\color{blue}{\text{m} \ \angle AEB}& =\dfrac {\color{green}{\text{m} \overset{\huge\frown}{ {AB}}}- \color{red}{\text{m} \overset{\huge\frown}{{CD}}}}{2}\end{align}|
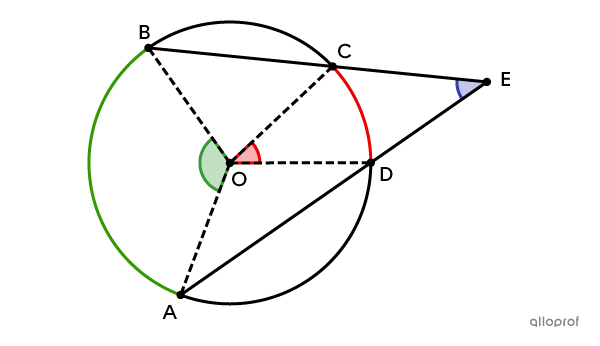
What is the measure of |\color{blue}{\angle BGD}| knowing that the point |E| is the centre of the circle?

|\tan \theta = \dfrac{\sin \theta}{\cos \theta}|
|\cot \theta = \dfrac{\cos\theta}{\sin\theta}|
|\csc \theta = \dfrac{1}{\sin \theta}|
|\sec \theta =\dfrac{1}{\cos \theta}|
||\begin{alignat}{13}\cos^2\theta&+\sin^2\theta&&=\quad 1\\\\ 1\quad&+\tan^2\theta&&=\,\sec^2\theta\\\\ \cot^2\theta&+\quad 1&&=\,\csc^2\theta\end{alignat}||
Prove the following identity. ||\sec \theta - \cos \theta = \tan \theta \sin \theta||
To fully grasp the concepts associated with vectors, it is important to be familiar with the following vocabulary.
In a Cartesian plane, draw |color{red}{\overrightarrow u} = (-3, 8)| and then determine its norm and direction.
To understand the different operations on vectors, it is important to define the following concepts.
Addition and subtraction
If |\color{blue}{\overrightarrow u = (a,b)}| and |\color{red}{\overrightarrow v = (c,d)},| then |\color{blue}{\overrightarrow u} + \color{red}{\overrightarrow v} = (\color{blue}{a} + \color{red}{c}, \color{blue}{b}+ \color{red}{d}).|
Multiplying a vector by a scalar
If |\overrightarrow u = (\color{blue}{a}, \color{red}{b})| and |k| is a scalar, then |k \overrightarrow u = (k \color{blue}{a}, k \color{red}{b}).|
The scalar product
If |\color{blue}{\overrightarrow u = (a,b)}| and |\color{red}{\overrightarrow v = (c,d)}|, then |\color{blue}{\overrightarrow u} \cdot \color{red}{\overrightarrow v} = \color{blue}{a}\color{red}{c}+ \color{blue}{b}\color{red}{d}.|
The linear combination of two vectors
Consider |\color{blue}{\overrightarrow u}| and |\color{red}{\overrightarrow v}|, then it is possible to obtain |\color{green}{\overrightarrow w}| according to a linear combination such that |\color{green}{\overrightarrow w} = k_1 \color{blue}{\overrightarrow u} + k_2 \color{red}{\overrightarrow v}| with |\{k_1,k_2\} \in \mathbb{R}.|
Determine the values for the scalars |\{k_1,k_2\}| so that |\color{blue}{\overrightarrow w = (4,-12)}| is the result of a linear combination of |\color{red}{\overrightarrow u = (-1,4)}| and |\color{green}{\overrightarrow v = (2,5)}.|
To solve this type of situation, it is important to have a good grasp of the various steps involved in operations on vectors and trigonometric ratios in right-angled triangles. The following steps can generally be followed.
Show the situation.
Place the data in the right places in the illustration.
Find the missing measurements using the Pythagorean relation or the trigonometric ratios in the right triangle.
After a violent storm, a tree has fallen onto the road leading to Julien's cottage. To clear the way, he ties a rope around the base of the tree to pull it out of the way.
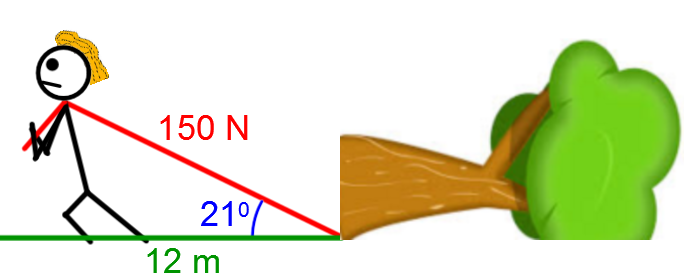
How much work will Julien have to do to displace the tree over a distance of |12\ \text{m}| if he exerts a force of |150\ \text{N}| and the chord he is using forms an angle of |21^\circ| with the horizontal, neglecting the force of friction?
Considering |(x, y)| as the coordinates of the point undergoing the rotation:
|r_{(O,90^\circ)}| or |r_{(O,-270^\circ)} : (x , y) \mapsto (-y , x)| for a rotation of |90^\circ| or |-270^\circ;|
|r_{(O,180^\circ)}| or |r_{(O,-180^\circ)} : (x , y) \mapsto (-x , -y)| for a rotation of |180^\circ| or |-180^\circ;|
|r_{(O,270^\circ)}| or |r_{(O,-90^\circ)} : (x , y) \mapsto (y , -x)| for a rotation of |270^\circ| or |-90^\circ.|
Given that the coordinates of the initial vertices of an |ABC| triangle are |A(3,2),| |B(-1,5)| and |C(4,-1),| determine the coordinates of the vertices in its image if it is rotated by |270^\circ.| centred at its origin.
If we take |(x, y)| to be the coordinates of the point undergoing the reflection:
the x-coordinate axis: |s_x : (x , y) \mapsto (x , -y);|
the y-coordinate axis: |s_y: (x , y) \mapsto (-x , y);|
the bisector of quadrants 1 and 3: |s_/: (x , y)\mapsto (y , x);|
the bisector of quadrants 2 and 4: |s_{\backslash}: (x , y) \mapsto (-y , -x).|
What is the image of the following quadrilateral when reflected from the y-axis?
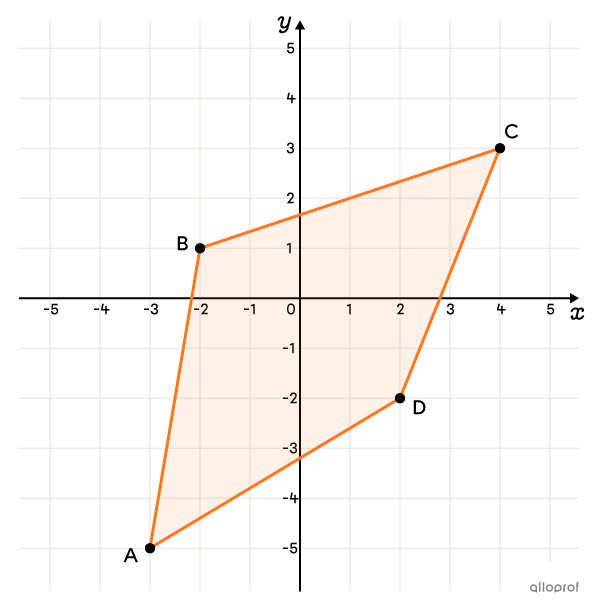
Considering |(x, y)| as the coordinates of the point undergoing the translation:
|t_{(a,b)}:(x,y) \mapsto (x+a,y+b)|
To create an interesting pattern on a tapestry, we use translation to repeat the same geometric figure over and over again. Using a Cartesian plane, we can establish that the initial coordinates of the vertices are |A(2,3),| |B(4,7),| |C(8,-2)| and |D(-3,12)| and that the final coordinates are |A'(7,-1),| |B’(9,3),| |C'(12,-6)| and |D’(2,-8).|
Knowing that the translation |t_{(5,-4)}| has been used, verify whether the initial and image figures are isometric.
Considering |(x, y)| as the coordinates of the point which undergoes the dilation:
|h_{(O,k)}:(x,y) \mapsto (kx, ky)|
On a map of the world, you see a very small island that catches your eye. To find out more about it, you first want to draw a larger version using a dilation defined by |H_{(O,12)}.| Initially, the coordinates of the endpoints of this island were |A(1,2),| |B(2,3),| |C(4,0),| |D(3,-2)| and |E(-1,-2).|
What would be the coordinates of this island once it was enlarged?
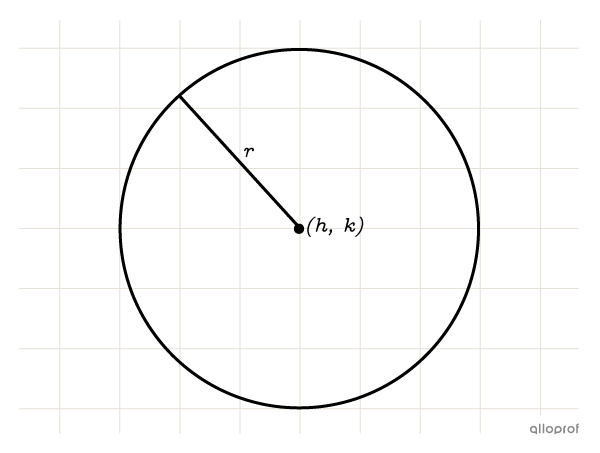
|(x-h)^2 + (y-k)^2 = r^2|
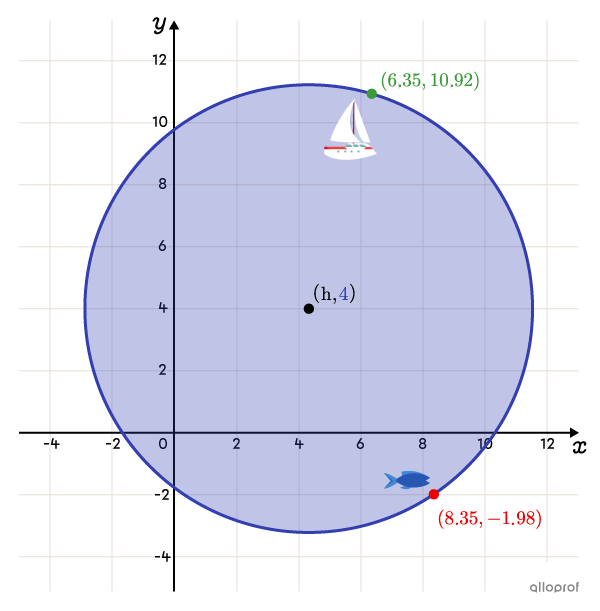
On her first fishing trip, Gitane uses sonar to locate potential catches. However, she's wondering about the range of the sonar. Using the information presented in the drawing below, determine the area, in |\text{km}^2,| covered by her sonar.
|\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1|
where
|\begin{align} a &:\text{half-measure of the horizontal axis}\\ b &: \text{half-measure of the vertical axis}\\ (h,k) & : \text{coordinates of the ellipse centre}\end{align}|
|\color{red}a < \color{blue}b|
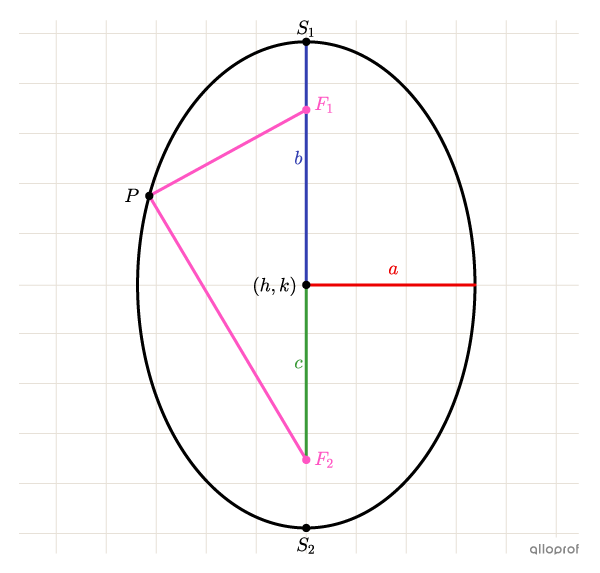
||\begin{align}\overline{\color{fuchsia}{F_1}P} + \overline{\color{fuchsia}{F_2}P} &= 2\color{green}{b}\\
\color{red}{a^2}+\color{green}{c^2} &= \color{blue}{b^2}\end{align}||
|\color{red}a > \color{blue}b|
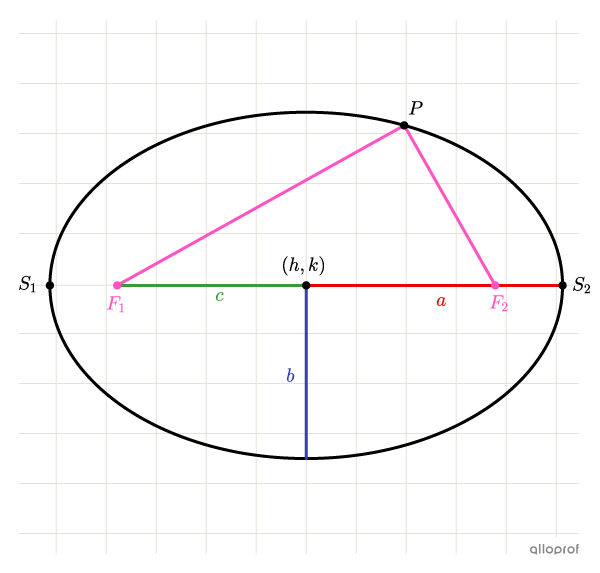
||\begin{align}\overline{\color{fuchsia}{F_1}P} + \overline{\color{fuchsia}{F_2}P} &= 2\color{red}{a}\\
\color{blue}{b^2}+\color{green}{c^2} &= \color{red}{a^2}
\end{align}||
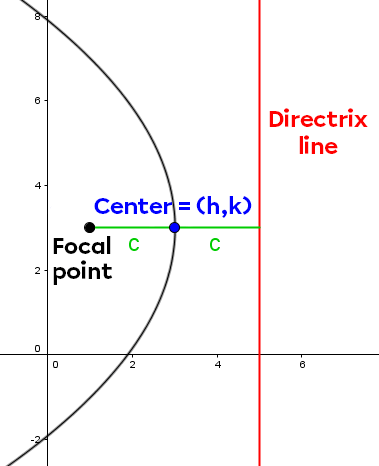
|(x-h)^2 = \pm 4 c (y-k)|
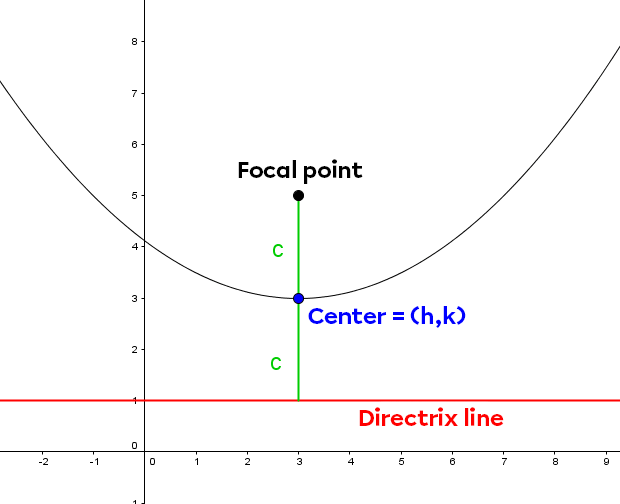
|(y-k)^2 = \pm 4 c (x-h)|
To get an idea of the size of the fish, Gitane has noticed that she can rely on the curve of her fishing rod as the fish takes the bait. Using the sonar she bought earlier, she can deduce the following information.
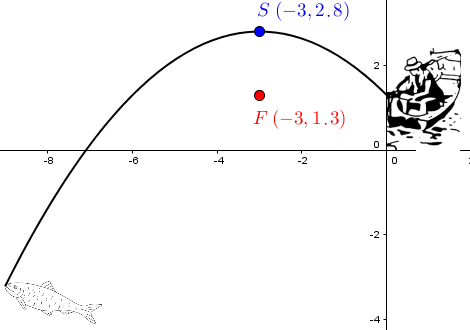
Since this situation presents a parabola, Gitane wonders what equation could be used to model it.
|\dfrac{(x-h)^2}{a^2} - \dfrac{(y-k)^2}{b^2} = -1|
where
|\begin{align} a &:\text{half the width of the rectangle}\\ b &: \text{the distance between a vertex and the centre} \\ (h,k)&:\text{the centre's coordinates}\\&\phantom {:}\ \ \text{(the intersection of the asymptotes)}\end{align}|
||\left \vert \text{m} \overline{F_1\color{orange}{P}} - \text{m} \overline{F_2\color{orange}{P}}\right \vert = \color{blue}{2b}\\ \color{red}{a^2}+\color{blue}{b^2}= \color{green}{c^2}||
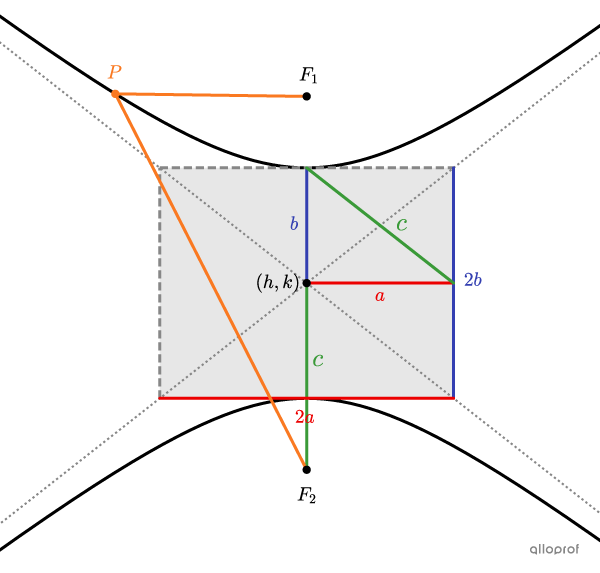
|\dfrac{(x-h)^2}{a^2} - \dfrac{(y-k)^2}{b^2}= 1|
where
|\begin{align} a &:\text{the distance between the vertex and the centre}\\ b &: \text{half the height of the rectangle} \\ (h,k)&:\text{the centre's coordinates}\\&\phantom {:}\ \ \text{(the intersection of the asymptotes)}\end{align}|
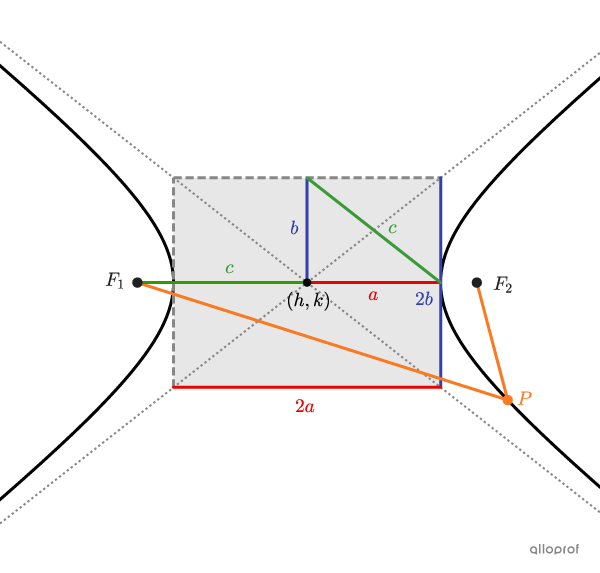
||\left \vert \text{m} \overline{F_1\color{orange}{P}} - \text{m} \overline{F_2\color{orange}{P}}\right \vert = \color{red}{2a}\\ \color{red}{a^2}+\color{blue}{b^2}= \color{green}{c^2}||
The rate of change of the asymptotes is equivalent to |\pm \dfrac{\color{blue}{b}}{\color{red}{a}}(x-h)+k.|
Finally, Gitane decided to head for a river that was a little busier. To her great misfortune, she noticed that she was being overtaken by two boats at the same time. To avoid capsizing, she has to displace her boat from the point where the two swells formed by the boats meet. This can be represented as follows.
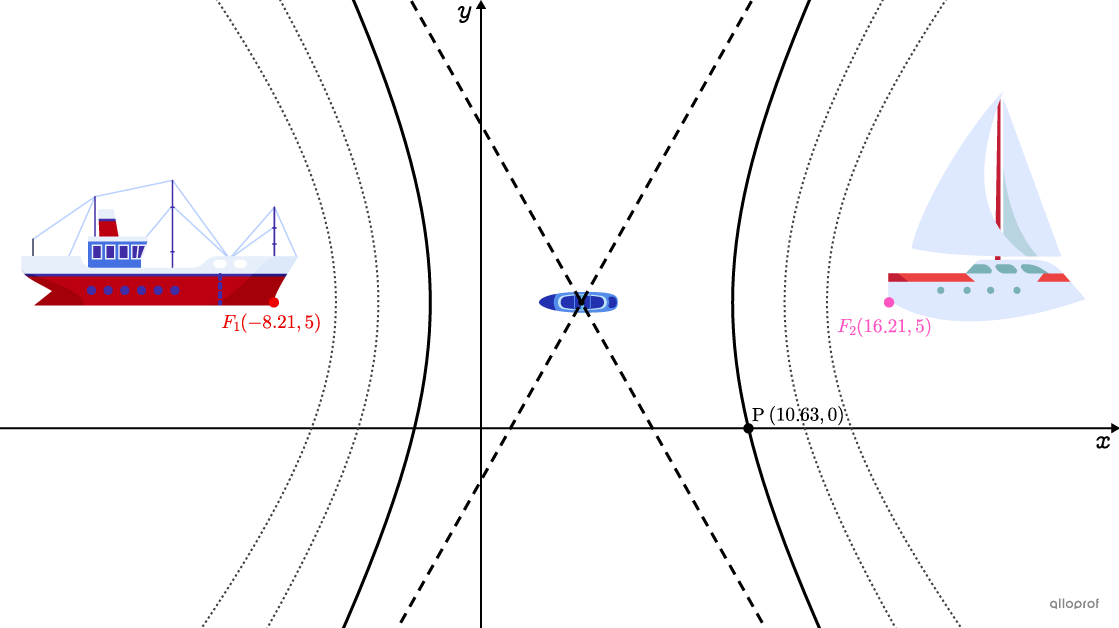
Using this data, determine the equation associated with the mathematical model that will enable Gitane to better orientate its navigation.
This involves solving a system of equations, generally using the substitution method.
A little fed up with fishing, Gitane decides to treat herself to a trip to a region where you can go boating with sharks that look like prehistoric sea dinosaurs. With the water practically transparent, she can see them swimming without any problem. However, she loses sight of them as they pass under the boat.
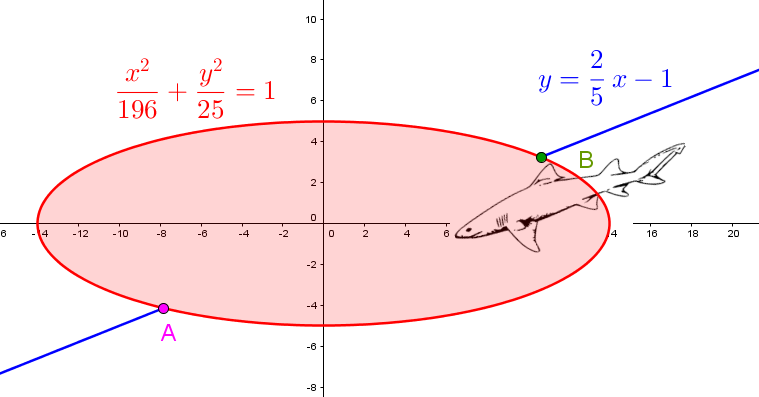
Assuming they swim in a straight line at a speed of |5| m/s, determine how long the sharks are under the ship.
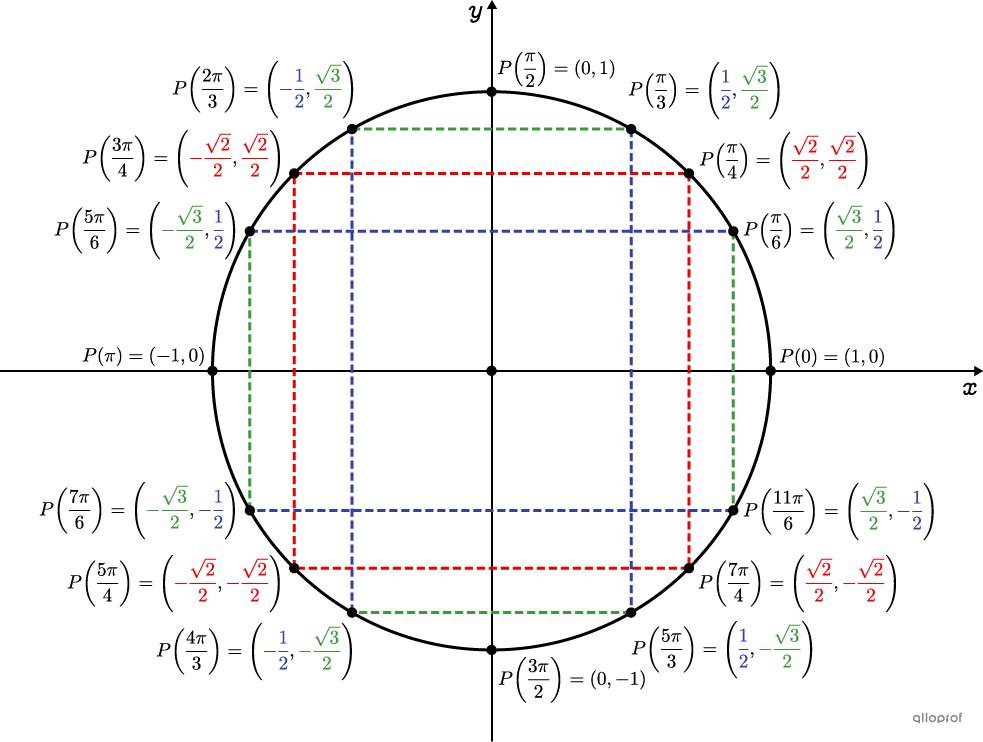
From this drawing, it's important to note two things.
The coordinates of points of the same colour are symmetrically related.
One complete turn of the circle |=2\pi\ \text{rad}.|
What are the coordinates of the point associated with an angle of |\dfrac{-17\pi}{4}?|