Matières
Niveaux
Voici un petit guide de préparation contenant toutes les notions abordées en cinquième secondaire dans la séquence TS. Pour expliquer le tout, chaque formule sera suivie d'un exemple et d'un lien qui mène à une fiche sur notre site.
Voici les lois et propriétés des exposants qui seront utiles pour la suite de cette section.
|a^{-m} = \dfrac{1}{a^m}|
|a^{\dfrac{m}{n}} = \sqrt[n]{a^m}|
|a^m \times a^n = a ^{m+n}|
|\dfrac{a^m}{a^n} = a^{m-n}|
|(ab)^m = a^m b^m|
|\left(\dfrac{a}{b}\right)^m = \dfrac{a^m}{b^m}|
|(a^m)^n = a^{m n}|
Simplifie au maximum l'expression suivante.||\dfrac{(27 a^3 b)^{\frac{1}{2}}}{27^{\frac{1}{3}}a^3}||
De façon générale, c'est la loi sur la multiplication des radicaux qui est utilisée pour effectuer la factorisation |(\sqrt { a \times b} = \sqrt{a} \times \sqrt{b}).| Pour y arriver, on doit :
décomposer le radicande en un produit de facteurs dont un est un nombre carré;
transformer la racine d'un produit en un produit de racines |(\sqrt{a \times b} = \sqrt{a} \times\sqrt{b});|
calculer la racine du nombre carré.
Quelle est la valeur simplifiée de la racine suivante?
||\sqrt{45}||
Voici les lois des logarithmes qu'il est important de maitriser.
|\log_c(M \times N) = \log_c M + \log_c N|
|\log_{c}\left(\dfrac{M}{N}\right)=\log_{c}M-\log_{c}N|
|\log_{\dfrac{_{1}}{c}}M=-\log_{c}M|
|\log_c M^n = n \log_c M|
|\log_a b = \dfrac{\log_c b}{\log_c a}|
En utilisant les lois des logarithmes, simplifie l'expression suivante. ||(\log_4 3x^2 + \log_4 4y - \log_4 6x)^4||
Pour trouver les valeurs de |x|, si elles existent, on peut utiliser une des trois formes suivantes.
La forme générale
|0 = ax^2 + bx + c|, avec cette formule : |\{x_1, x_2\}= \dfrac{-b \pm \sqrt{b^2-4ac}}{2a}.|
La forme canonique
|0 = a(x-h)^2+k|
où |(h,k) =| coordonnée du sommet et on isole le |x| avec les opérations inverses.
La forme factorisée
|0 = a(x-z_1)(x-z_2)|
où |\{z_1,z_2\}=| zéros de la fonction et on obtient deux équations : |x-z_1 = 0 | et |x-z_2=0.|
Lors des Jeux Olympiques d'été en 2012, le britannique Greg Rutherford a effectué le saut suivant.
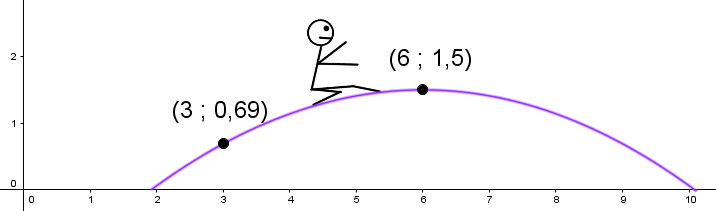
En considérant que son saut suit un modèle parabolique, détermine la distance du saut de Greg.
On peut résoudre une inéquation en lien avec ce modèle en suivant les mêmes étapes tout en ajoutant une des étapes suivantes.
Faire une représentation graphique de la situation.
Vérifier l'inéquation à l'aide d'un point.
En effet, l'intervalle-solution d'une inéquation est en lien direct avec l'équation qui lui est associée.
|f(x) = a \log_c (b(x-h))|
où
|\dfrac{1}{b} + h=| le zéro de fonction,
|h = | l'asymptote.
Soit la fonction suivante.
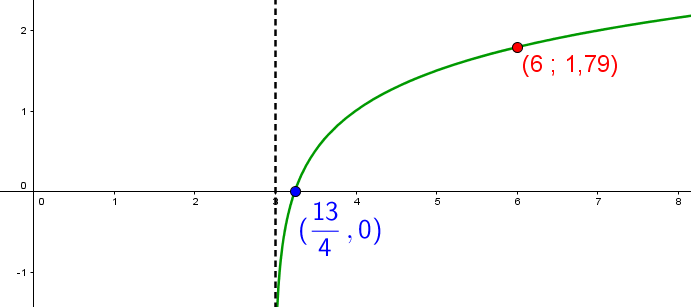
Quelle est la valeur de l'abscisse si l'ordonnée vaut 3?
On peut résoudre une inéquation en lien avec ce modèle en suivant les mêmes étapes tout en ajoutant une des étapes suivantes.
Faire une représentation graphique de la situation.
Vérifier l'inéquation à l'aide d'un point.
En effet, l'intervalle-solution d'une inéquation est en lien direct avec l'équation qui lui est associée.
|f(x) = a c ^{bx} + k|
où
|b = | fréquence de capitalisation,
|k = | asymptote,
| c = 1\,\pm| pourcentage de variation en nombre décimal.
Lorsqu'un placement est fait dans une institution bancaire, son rendement est généralement évalué selon une fonction exponentielle. Par contre, pour bénéficier de certains taux qui sont plus avantageux, une somme minimale d'investissement est requise.
Ainsi, après combien d'années un investissement initial de |5\ 000\ $| capitalisé aux |2| ans à un taux d'intérêt de |5| % dont l'investissement minimal requis est de |3\ 000\ $| rapporte-il au moins |8\ 000\ $?|
On peut résoudre une inéquation en lien avec ce modèle en suivant les mêmes étapes tout en ajoutant une des étapes suivantes.
Faire une représentation graphique de la situation.
Vérifier l'inéquation à l'aide d'un point.
En effet, l'intervalle-solution d'une inéquation est en lien direct avec l'équation qui lui est associée.
|f(x) = a \sqrt{b(x-h)} + k|
où
|(h,k) = | coordonnée du sommet,
|b = | généralement |\pm 1,|
les signes de |a| et |b| dépendent de l'orientation de la courbe.
En tant qu'ornithologue amateur(-trice), tu observes un oiseau prendre son envol à partir d'une branche qui est à trois mètres du sol. Sa trajectoire suit le modèle suivant.
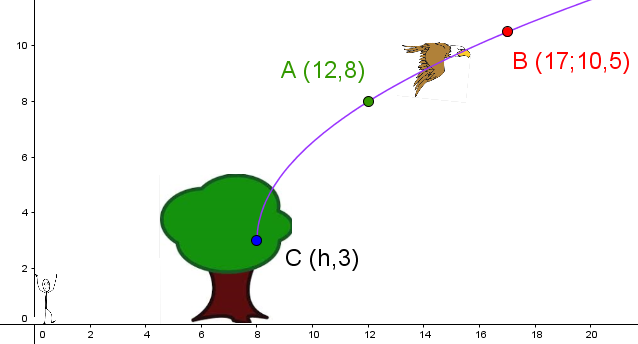
Sachant qu'il est toujours possible d'observer l'oiseau alors qu'il est à une altitude de |50\ \text{m},| quelle sera la distance horizontale qui te séparera de l'oiseau à ce moment précis?
On peut résoudre une inéquation en lien avec ce modèle en suivant les mêmes étapes tout en ajoutant une des étapes suivantes.
Faire une représentation graphique de la situation.
Vérifier l'inéquation à l'aide d'un point.
En effet, l'intervalle-solution d'une inéquation est en lien direct avec l'équation qui lui est associée.
Sous sa forme canonique : |f(x) = \dfrac{a}{b(x-h)} + k|
Sous sa forme de quotient : |f(x) = \dfrac{ax+b}{cx+d}|
Selon les informations disponibles dans le graphique, détermine les coordonnées complètes du point |\color{red}{B}.|
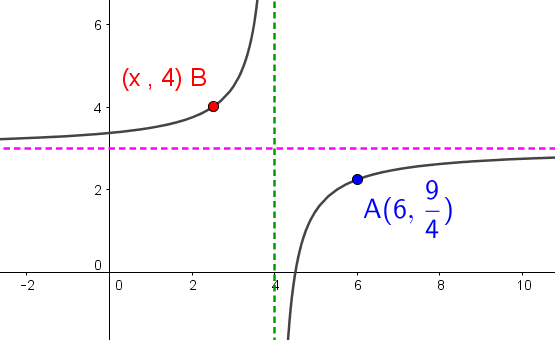
On peut résoudre une inéquation en lien avec ce modèle en suivant les mêmes étapes tout en ajoutant une des étapes suivantes.
Faire une représentation graphique de la situation.
Vérifier l'inéquation à l'aide d'un point.
En effet, l'intervalle-solution d'une inéquation est en lien direct avec l'équation qui lui est associée.
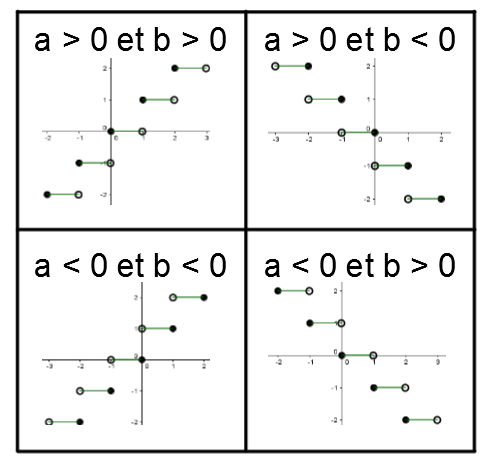
L'équation de la règle d'une fonction partie entière s'écrit sous la forme suivante. ||f(x) = a \left[ b(x-h)\right] + k|| où
|(h,k) =| coordonnées d'un point plein,
|\vert a\vert = | distance verticale entre deux marches,
|\dfrac{1}{\vert b \vert} = | longueur d'une marche.
Pour déterminer le signe de |a| et de |b,| on doit s'intéresser à l'ordre des points ouverts et fermés, à la croissance et à la décroissance du graphique.
Dans le cadre d'un nouveau programme de récompense, une épicerie offre des timbres qui permettent d'obtenir des réductions significatives sur l'achat d'articles ciblés.
Avec un montant d'achat minimum de 5 $, la caissière remet cinq timbres aux clients. Par la suite, pour chaque tranche de 22 $ additionnels, elle donne sept timbres de plus au client.
À l'aide de ces informations, dans quel intervalle devrait se situer le montant de la prochaine facture d'un client s'il veut obtenir 47 timbres?
On peut résoudre une inéquation en lien avec ce modèle en suivant les mêmes étapes tout en ajoutant une des étapes suivantes.
Faire une représentation graphique de la situation.
Vérifier l'inéquation à l'aide d'un point.
En effet, l'intervalle-solution d'une inéquation est en lien direct avec l'équation qui lui est associée.
En fonction de la situation, on peut choisir parmi trois modèles de fonctions trigonométriques.
|f(x) = a \cos (b (x-h)) + k|
|g(x) = a \sin(b (x-h)) + k|
|h(x) = a \tan(b (x-h)) + k|
Pour divertir ton chien, tu décides d'aller jouer dehors avec lui à son jeu favori, soit « rapporte la ba-balle ». Te situant maintenant à 10 mètres de la maison, tu t'assures de toujours lancer la « ba-balle » 30 mètres plus loin. De plus, tu as remarqué qu'à cette distance, ton chien met 12 secondes pour aller la chercher et te la rapporter. Bien entendu, tu relances la balle aussitôt qu'il te la rapporte et ce, pendant cinq minutes.
Par contre, ton chien n'est pas parfaitement dressé. Ainsi, tu as peur qu'il s'enfuit quand il se trouve à plus de 30 mètres de la maison. En tenant compte de ces informations, pendant combien de temps durant ce jeu as-tu peur que ton chien s'enfuit?
On peut résoudre une inéquation en lien avec ce modèle en suivant les mêmes étapes tout en ajoutant une des étapes suivantes.
Faire une représentation graphique de la situation.
Vérifier l'inéquation à l'aide d'un point.
En effet, l'intervalle-solution d'une inéquation est en lien direct avec l'équation qui lui est associée.
Pour effectuer les opérations sur les fonctions, on utilise les mêmes concepts que ceux abordés pour la simplification d'expressions algébriques.
Addition et soustraction
Sur les coefficients des termes semblables
Multiplication et division
Sur les coefficients de tous les termes et en respectant les lois des exposants
Pour certains investisseurs, spéculer sur les diverses valeurs boursières à la bourse est une vraie passion. Pour essayer de prédire les valeurs des différentes actions et les profits potentiels, ces gens utilisent différents graphiques pour ensuite les associer à des modèles mathématiques. Pour l'étude d'une certains compagnie étrangère, on peut utiliser les fonctions suivantes pour modéliser les différentes variables qui influencent le rendement final de chaque action.
Nombre d'actions sur le marché : |f(x) = 10x - 500|
Profit d'une action : |g(x) = -x^2+160x - 6\ 400|
Nombre d'actionnaires : |h(x)= -2x^2 + 260x - 8\ 000|
où |x :| nombre d'années écoulées depuis sa création
Quelle fonction pourrait-on utiliser pour déterminer le profit moyen obtenu par chaque actionnaire?
La composition de fonction se note |g \circ f = g\big(f(x)\big)| et |g \circ f| se lit « |g| rond |f| ».
Afin d'établir leur budget pour la prochaine année, le comité d'administration d'Alloprof s'est penché sur les couts de production des fiches de la bibliothèque virtuelle. Pour ce faire, ils ont utilisé deux fonctions :
fonction f : |t = \dfrac{5}{4} n|
fonction g : |s = 124t + 2\ 000|
où |n = | nombre de fiches produites, |t=| le nombre d'heures travaillées et |s = | salaire (en $) à verser aux employés.
Modélise cette situation à l'aide d'une seule fonction pour ensuite déterminer le nombre total de fiches qu'il serait possible de produire avec un budget de 13 625 $.
Généralement, on peut résoudre un problème d'optimisation en suivant les étapes suivantes.
Identifier les variables et les inconnus.
Déterminer l'équation de la fonction à optimiser.
Créer le système d'inéquations.
Tracer le polygone de contraintes.
Déterminer les coordonnées de chacun des sommets de ce polygone.
Déterminer les coordonnées du point qui optimise la fonction.
Afin de maximiser les profits de son entreprise, un directeur général tient à savoir combien de vestons et de chemises il doit vendre chaque semaine. À cause de certaines contraintes de production, il sait que le nombre maximal de chemises correspond au retranchement du quadruple de vestons à 21. À cause du transport, le nombre de vestons doit être plus grand ou égal à la différence entre 8 et le triple du nombre de chemises. Finalement, le reste entre le triple du nombre de vestons et le double du nombre de chemises doit être d'au moins deux.
En sachant que chaque veston vendu rapporte un profit de |32| $ et que celui associé à la vente d'une chemise est de |17| $, quel est le profit maximal hebdomadaire qu'il peut espérer obtenir?
Deux figures sont équivalentes lorsqu'elles ont la même aire.
Afin que le cout d'asphaltage de son nouveau stationnement résidentiel soit le même que celui de son ancien, Julien veut que ses deux entrées soient équivalentes.
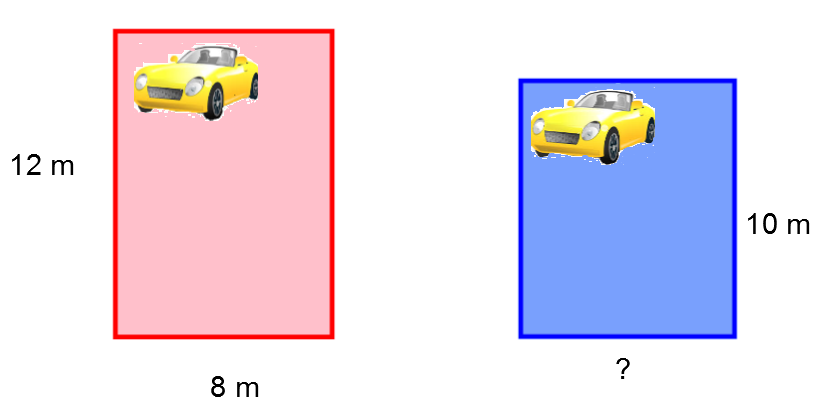
Ainsi, quelle devrait être la mesure de la largeur de son nouveau stationnement?
Deux solides sont équivalents lorsqu'ils ont le même volume.
Une compagnie qui œuvre dans les accessoires de plein air veut offrir deux modèles de tente différents. Afin de conserver les mêmes couts de production, la compagnie tient à ce que ces deux modèles soient équivalents.
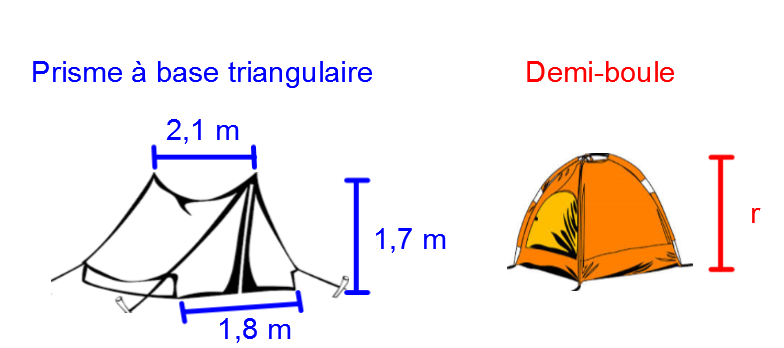
Quelle devrait être la mesure de la hauteur du second modèle afin de respecter la condition de similitude?
Un angle d'une mesure d'un radian correspond à l'angle au centre formé par un arc de cercle dont la mesure est équivalente au rayon.
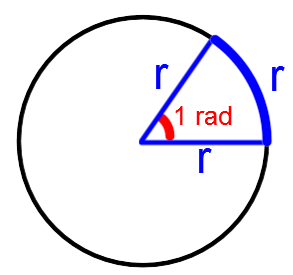
Par ailleurs, on peut utiliser la proportion suivante pour transformer une mesure en degrés en une mesure en radians et vice versa. ||\dfrac{\text{Mesure de l'angle en degrés}}{180^\circ} = \dfrac{\text{Mesure de l'angle en radians}}{\pi \text{ rad}}||
Si un angle mesure |\color{red}{227^\circ},| quelle est sa mesure en radians?
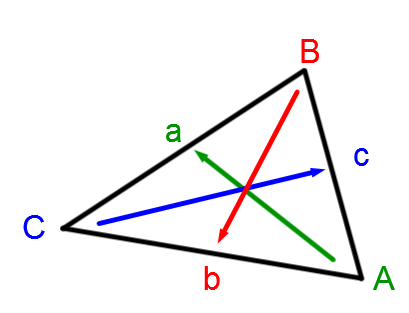
Selon le triangle quelconque qui suit, on peut déduire une série d'équivalences.
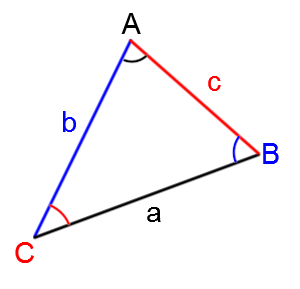
||\dfrac{a}{\sin A} = \dfrac{b}{\sin B} =\dfrac{c}{\sin C}||
Lors de certaines festivités westerns, des courses de chevaux sont organisées pour animer le spectacle. Lors de ces courses, les cowboys doivent faire le tour de chacun des trois barils qui sont disposés en forme de triangle isocèle.
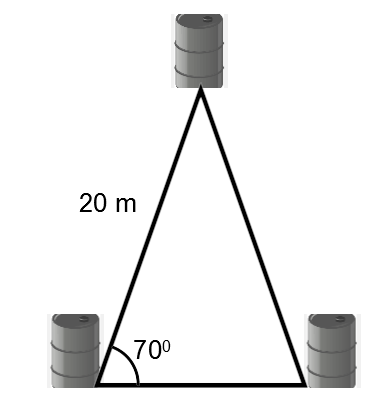
À l'aide des mesures données, quelle est la distance entre chacun des barils?
Afin d'assurer un aérodynamisme maximal, le profil de certaines voitures de course ressemble à un triangle.
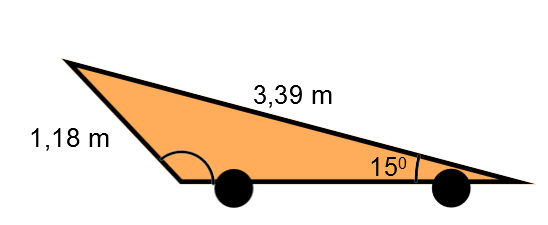
Afin que ces proportions soient conservées, quelle devrait être la mesure de l'angle qui se situe près de la roue arrière?
Quand on identifie le triangle, il est toujours essentiel de mettre :
|\color{green}{\text{le côté a opposé à l'angle A}};|
|\color{red}{\text{le côté b opposé à l'angle B}};|
|\color{blue}{\text{le côté c opposé à l'angle C}}.|
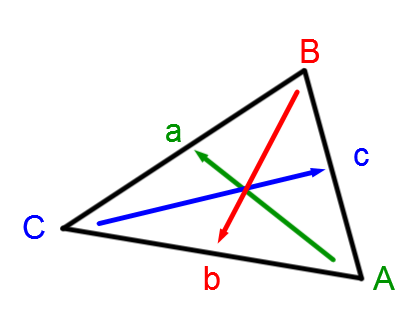
Selon le triangle quelconque qui suit, on peut déduire trois équivalences.

||a^2 = \color{blue}{b}^2 + \color{red}{c}^2 - 2 \color{blue}{b} \color{red}{c} \cos A||
||\color{blue}{b}^2 = a^2 + \color{red}{c}^2 - 2 a \color{red}{c} \cos \color{blue}{B}||
||\color{red}{c}^2 = a^2 + \color{blue}{b}^2 - 2 a \color{blue}{b} \cos \color{red}{C}||
Afin de maximiser ses chances de chasser un orignal, un chasseur à l'arc s'installe dans un coin de son terrain et la portée de ses flèches se décrit selon le triangle suivant.
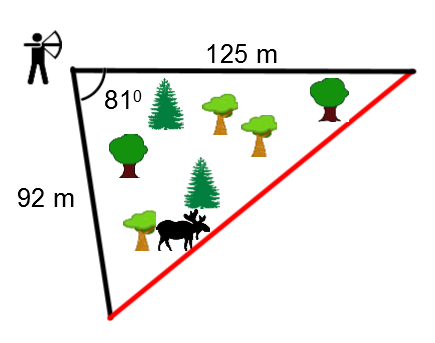
En te fiant aux informations sur ce dessin, sur quelle distance est-ce que l'orignal peut se promener en restant le plus loin possible du chasseur?
Afin d'assurer la sécurité de ses employés et employées, une banque fait installer une caméra de surveillance rotative dans le hall d'entrée. Par ailleurs, un agent de sécurité est également chargé de surveiller cette même région qui est définie par le triangle suivant.
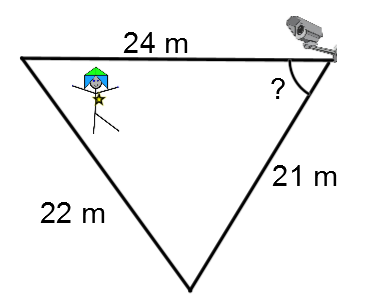
Afin de s'assurer qu'il n'y ait aucun angle mort, quelle devrait être la mesure de l'angle de rotation de la caméra?
Quand on identifie le triangle, il est toujours essentiel de mettre :
|\color{green}{\text{le côté a opposé à l'angle A}};|
|\color{red}{\text{le côté b opposé à l'angle B}};|
|\color{blue}{\text{le côté c opposé à l'angle C}}.|
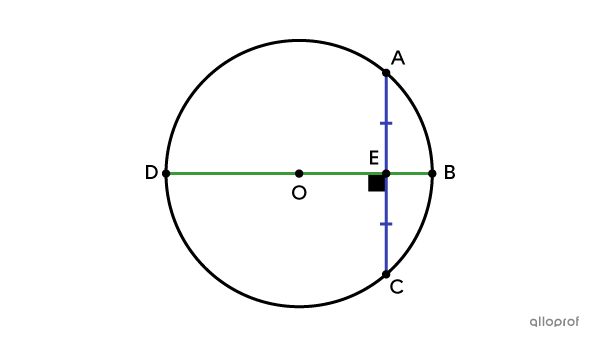
Si |\color{green}{\overline{BD}} \perp \color{blue}{\overline{AC}}| et |\color{green}{\overline{BD}}| est un diamètre, alors |\color{blue}{\overline{AC}}| est divisée en deux parties égales.
Si |\color{blue}{\overline{AD}}| et |\color{red}{\overline{BC}}| sont à égale distance du centre, alors |\text{m} \ \color{blue}{\overline{AD}} = \text{m} \ \color{red}{\overline{BC}}.|

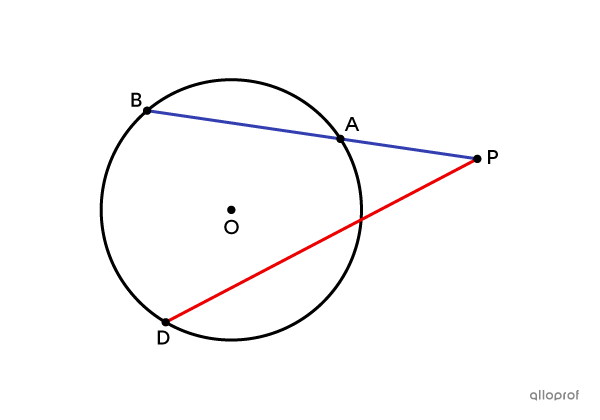
|\text{m} \ \color{blue}{\overline{PA}} \times \ \text{m} \ \color{blue}{\overline{PB}} = \text{m} \ \color{red}{\overline{PC}} \times \ \text{m} \ \color{red}{\overline{PD}}|
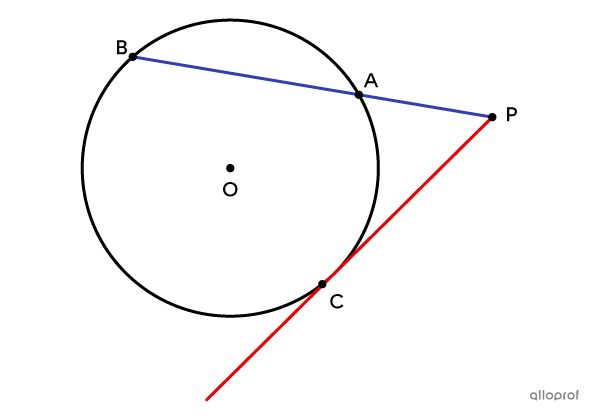
|\text{m}\ \color{blue}{\overline{PA}} \times \ \text{m} \ \color{blue}{\overline{PB}} = \text{m} \ \color{red}{\overline{PC}}^2|
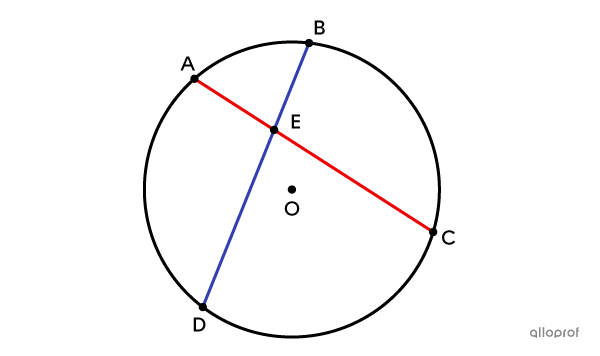
|\text{m} \ \color{red}{\overline{AE}} \times \ \text{m}\ \color{red}{\overline{CE}} = \text{m}\ \color{blue}{\overline{BE}} \times \text{m}\ \color{blue}{\overline{DE}}|
En sachant que |\overline{BF}| est un diamètre, quelle est la mesure de |\color{fuchsia}{\overline{FI}}?|

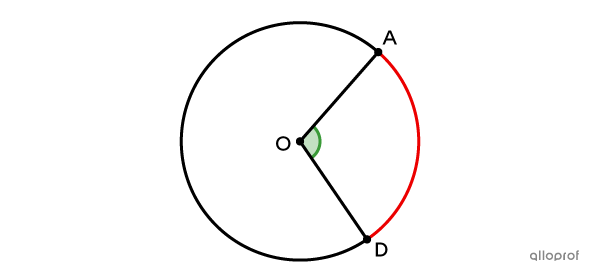
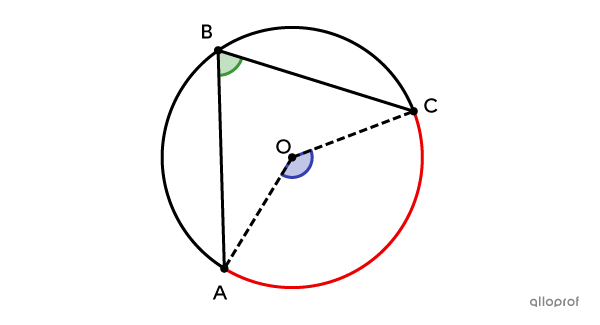
Il est important de noter que |\text{m} \ \overset{\ \huge\frown}{{AD}}| fait référence à la mesure de l'angle au centre qui intercepte l'arc en question.||\text{m} \ \overset{\ \huge\frown}{{\color{red}{AD}}} = \text{m} \ \color{green}{\angle AOD}||
|\begin{align}\color{green}{\text{m} \ \angle ABC} &= \dfrac{\color{blue}{\text{m}\ \angle AOC}}{2}\\\color{green}{\text{m}\ \angle ABC} &= \dfrac{\color{red}{\text{m} \overset{\ \huge\frown}{{AC}}}}{2}\end{align}|
|\begin{align}\color{green}{\text{m} \ \angle AEB} &= \dfrac{\color{red}{\text{m} \ \angle AOB} + \color{blue}{\text{m} \ \angle COD}}{2}\\
\color{green}{\text{m} \ \angle AEB} &= \dfrac {\color{red}{\text{m}\ \overset{ \huge\frown}{ {AB}}}+ \color{blue}{\text{m}\ \overset{ \huge\frown}{{CD}}}}{2}\end{align}|

|\begin{align}\color{blue}{\text{m} \ \angle AEB} &=\dfrac{\color{green}{\text{m} \ \angle AOB} - \color{red}{\text{m} \ \angle COD}}{2}\\
\color{blue}{\text{m} \ \angle AEB}& =\dfrac {\color{green}{\text{m} \overset{\huge\frown}{ {AB}}}- \color{red}{\text{m} \overset{\huge\frown}{{CD}}}}{2}\end{align}|
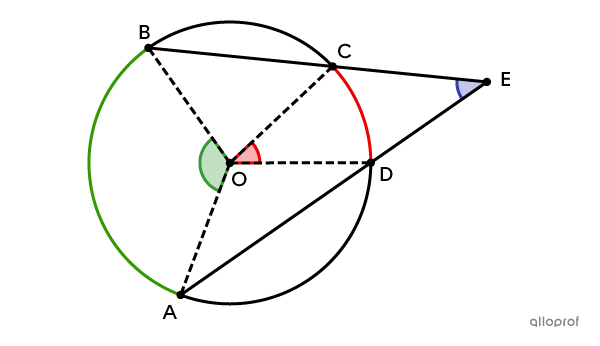
Quelle est la mesure de |\color{blue}{\angle BGD}| sachant que le point |E| est le centre du cercle?

||\begin{align}\tan\theta &= \dfrac{\sin\theta}{\cos\theta}\\\\ \text{cotan }\theta &= \dfrac{\cos\theta}{\sin\theta}\\\\ \text{cosec }\theta &= \dfrac{1}{\sin\theta} \\\\ \sec\theta &=\dfrac{1}{\cos\theta}\end{align}||
||\begin{alignat}{13}\cos^2\theta\ \,&+\,\sin^2\theta&&=\quad\ 1\\\\ 1\quad\ \,&+\tan^2\theta&&=\ \sec^2\theta\\\\ \text{cotan}^2\theta&+\quad1&&=\text{cosec}^2\theta\end{alignat}||
Démontrer l'identité suivante. ||\sec \theta - \cos \theta = \tan \theta \sin \theta||
Pour bien saisir les notions associées au concept des vecteurs, il est important de bien maitriser le vocabulaire suivant.
L'orientation d'un vecteur est représentée par un sens (flèche) et par une direction (inclinaison associée à une mesure en degrés).
La direction d'un vecteur est toujours calculée selon l'axe des abscisses positives en allant dans le sens anti-horaire.
La norme d'un vecteur fait référence à la longueur du vecteur que l'on peut obtenir par des rapports trigonométriques ou par la relation de Pythagore.
Le travail effectué est associé à l'effort effectué pour déplacer une masse quelconque. Pour sa part, il est généralement mesuré en Joules.
Dans un plan cartésien, dessine |\color{red}{\overrightarrow u} = (-3, 8)| pour ensuite déterminer sa norme et sa direction.
Pour s'y retrouver dans les différentes opérations sur les vecteurs, il est important de bien définir les notions suivantes.
L'addition et la soustraction
Si |\color{blue}{\overrightarrow u = (a,b)}| et |\color{red}{\overrightarrow v = (c,d)},| alors |\color{blue}{\overrightarrow u} + \color{red}{\overrightarrow v} = (\color{blue}{a} + \color{red}{c}, \color{blue}{b}+ \color{red}{d}).|
La multiplication d'un vecteur par un scalaire
Si |\overrightarrow u = (\color{blue}{a}, \color{red}{b})| et |k| est un scalaire, alors |k \overrightarrow u = (k \color{blue}{a}, k \color{red}{b}).|
Le produit scalaire
Si |\color{blue}{\overrightarrow u = (a,b)}| et |\color{red}{\overrightarrow v = (c,d)}|, alors |\color{blue}{\overrightarrow u} \cdot \color{red}{\overrightarrow v} = \color{blue}{a}\color{red}{c}+ \color{blue}{b}\color{red}{d}.|
La combinaison linéaire de deux vecteurs
Soit |\color{blue}{\overrightarrow u}| et |\color{red}{\overrightarrow v}|, alors il est possible d'obtenir |\color{green}{\overrightarrow w}| selon une combinaison linéaire telle que |\color{green}{\overrightarrow w} = k_1 \color{blue}{\overrightarrow u} + k_2 \color{red}{\overrightarrow v}| avec |\{k_1,k_2\} \in \mathbb{R}.|
Détermine les valeurs des scalaires |\{k_1,k_2\}| de telle façon que |\color{blue}{\overrightarrow w = (4,-12)}| soit le résultat d'une combinaison linéaire de |\color{red}{\overrightarrow u = (-1,4)}| et |\color{green}{\overrightarrow v = (2,5)}.|
Pour résoudre ce genre de mise en situation, il est important de bien maitriser les diverses démarches associées aux opérations sur les vecteurs ainsi que les rapports trigonométriques dans les triangles rectangles. Par la suite, on peut généralement suivre les étapes suivantes.
Illustrer la mise en situation.
Placer les données aux bons endroits sur l'illustration.
Trouver les mesures manquantes à l'aide de la relation de Pythagore ou des rapports trigonométriques dans le triangle rectangle.
Après une violente tempête, un arbre est tombé sur la route qui mène au chalet de Julien. Pour libérer le passage, il attache une corde à la base de l'arbre afin de le tirer hors du chemin.
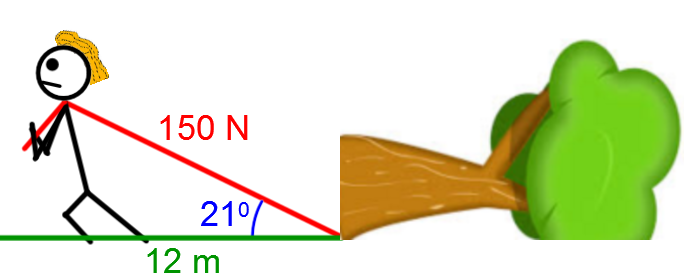
Quel travail devra effectuer Julien pour déplacer l'arbre sur une distance de |12 \ \text{m}| s'il déploie une force de |150 \ \text{N}| et que la corde qu'il utilise forme un angle de |21^\circ| par rapport à l'horizontal tout en négligeant la force de frottement?
En considérant |(x, y)| comme la coordonnée du point qui subit la rotation :
|r_{(O,90^\circ)}| ou |r_{(O,-270^\circ)} : (x , y) \mapsto (-y , x)| pour une rotation de |90^\circ| ou |-270^\circ;|
|r_{(O,180^\circ)}| ou |r_{(O,-180^\circ)} : (x , y) \mapsto (-x , -y)| pour une rotation de |180^\circ| ou |-180^\circ;|
|r_{(O,270^\circ)}| ou |r_{(O,-90^\circ)} : (x , y) \mapsto (y , -x)| pour une rotation de |270^\circ| ou |-90^\circ.|
En sachant que les coordonnées des sommets initiaux d'un triangle |ABC| sont |A(3,2),| |B(-1,5)| et |C(4,-1),| détermine les coordonnées des sommets de son image si on lui fait subir une rotation centrée à l'origine de |270^\circ.|
En considérant |(x, y)| comme la coordonnée du point qui subit la réflexion :
l’axe des abscisses : |s_x : (x , y) \mapsto (x , -y);|
l’axe des ordonnées : |s_y: (x , y) \mapsto (-x , y);|
la bissectrice des quadrants 1 et 3 : |s_/: (x , y)\mapsto (y , x);|
la bissectrice des quadrants 2 et 4 : |s_{\backslash}: (x , y) \mapsto (-y , -x).|
Quelle est l'image du quadrilatère suivant si on lui fait subir une réflexion par rapport à l'axe des ordonnées?
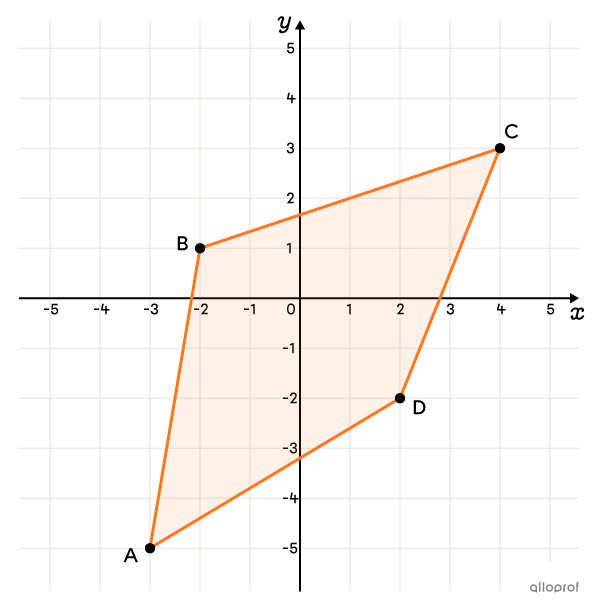
En considérant |(x, y)| comme la coordonnée du point qui subit la translation :
|t_{(a,b)}:(x,y) \mapsto (x+a,y+b).|
Dans le but de créer un motif intéressant sur une tapisserie, on se sert de la translation pour répéter la même figure géométrique à plusieurs reprises. En utilisant un plan cartésien, on peut établir que les coordonnées initiales des sommets sont |A(2,3),| |B(4,7),| |C(8,-2)| et |D(-3,12)| et que les coordonnées finales sont |A'(7,-1),| |B'(9,3),| |C'(12,-6)| et |D'(2,-8).|
En sachant que la translation |t_{(5,-4)}| a été utilisée, vérifie si les figures initiales et images sont isométriques.
En considérant |(x, y)| comme la coordonnée du point qui subit l'homothétie :
|h_{(O,k)}:(x,y) \mapsto (kx, ky).|
Sur une carte du monde, tu aperçois une très petite ile qui attire ton attention. Pour en apprendre plus à son sujet, tu veux d'abord en dessiner une plus grande version en utilisant une homothétie définie par |H_{(O,12)}.| Initialement, les coordonnées des extrémités de cette ile étaient |A(1,2),| |B(2,3),| |C(4,0),| |D(3,-2)| et |E(-1,-2).|
Quelles seraient les coordonnées de cette ile une fois celle-ci agrandie?
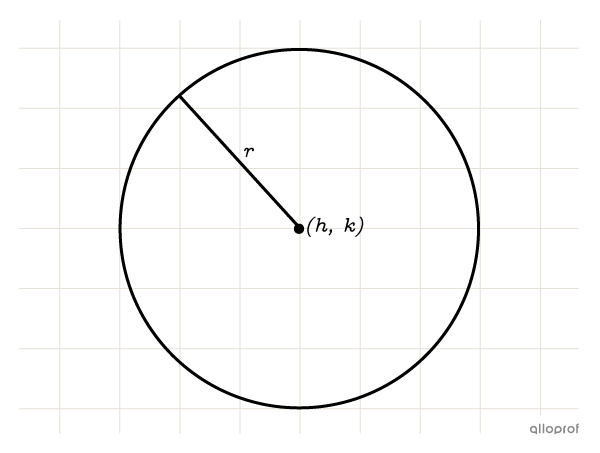
|(x-h)^2 + (y-k)^2 = r^2|
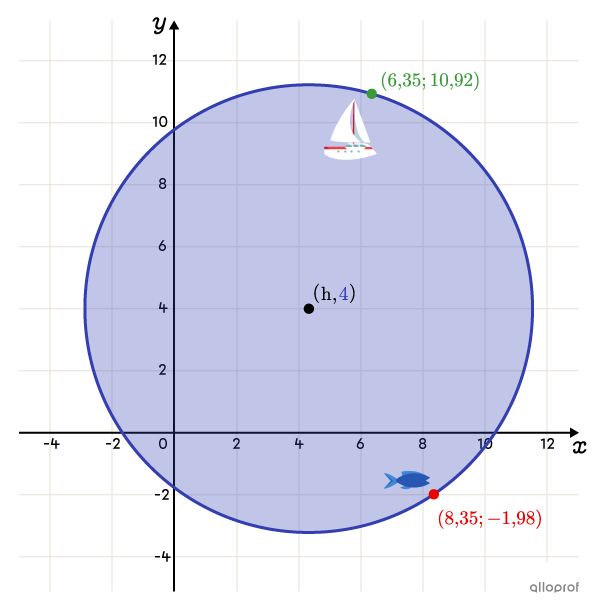
Pour son premier voyage de pêche, Gitane se sert d'un sonar pour localiser ses potentielles prises. Par contre, elle s'interroge sur la portée de celui-ci. En fonction des informations présentées sur le dessin ci-dessous, détermine la superficie, en |\text{km}^2,| couverte par son sonar.
|\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1|
où
|\begin{align} a &:\text{Demi-mesure de l'axe horizontal}\\ b &: \text{Demi-mesure de l'axe vertical}\\ (h,k) & : \text{Coordonnées du centre de l'ellipse}\end{align}|
|\color{red}a < \color{blue}b|
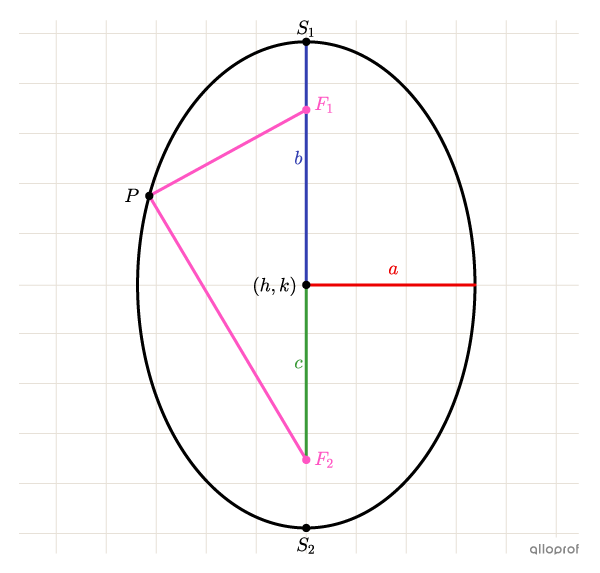
||\begin{align}\overline{\color{fuchsia}{F_1}P} + \overline{\color{fuchsia}{F_2}P} &= 2\color{green}{b}\\
\color{red}{a^2}+\color{green}{c^2} &= \color{blue}{b^2}\end{align}||
|\color{red}a > \color{blue}b|
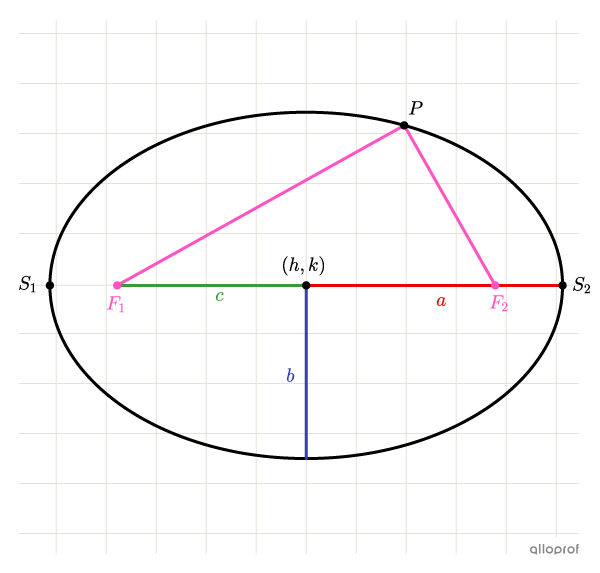
||\begin{align}\overline{\color{fuchsia}{F_1}P} + \overline{\color{fuchsia}{F_2}P} &= 2\color{red}{a}\\
\color{blue}{b^2}+\color{green}{c^2} &= \color{red}{a^2}
\end{align}||
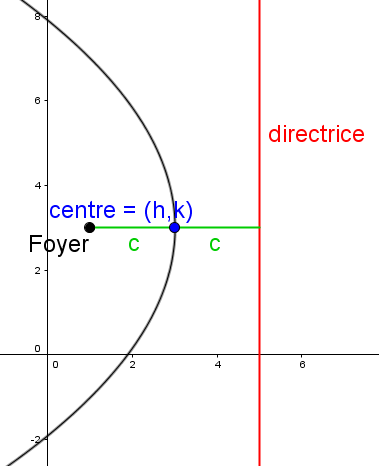
|(x-h)^2 = \pm 4 c (y-k)|
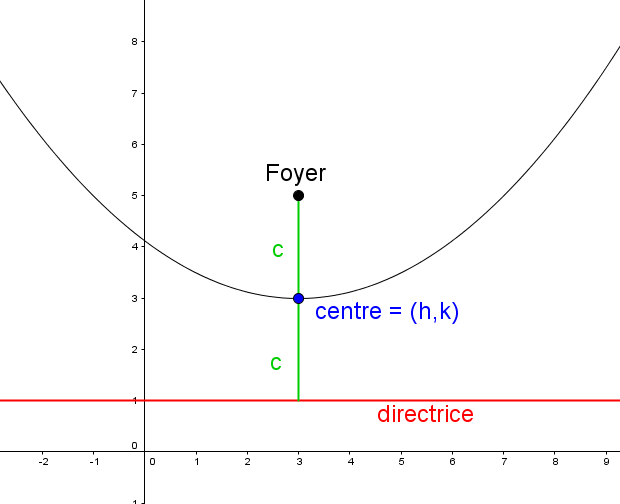
|(y-k)^2 = \pm 4 c (x-h)|
Pour avoir une idée de la grosseur du poisson, Gitane a remarqué qu'elle peut se fier à la courbure de sa canne à pêche au moment où le poisson mord à l'hameçon. En utilisant son sonar acheté précédemment, elle peut déduire les informations suivantes.
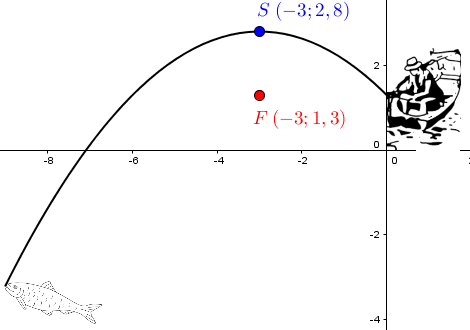
Cette situation présentant une forme parabolique, Gitane s'interroge sur l'équation qu'il est possible d'utiliser pour la modéliser.
|\dfrac{(x-h)^2}{a^2} - \dfrac{(y-k)^2}{b^2} = -1|
où
|\begin{align} a &:\text{la moitié de la largeur du rectangle}\\ b &: \text{la distance entre un sommet et le centre} \\ (h,k)&:\text{les coordonnées du centre}\\&\phantom {:}\ \ \text{(l'intersection des asymptotes)}\end{align}|
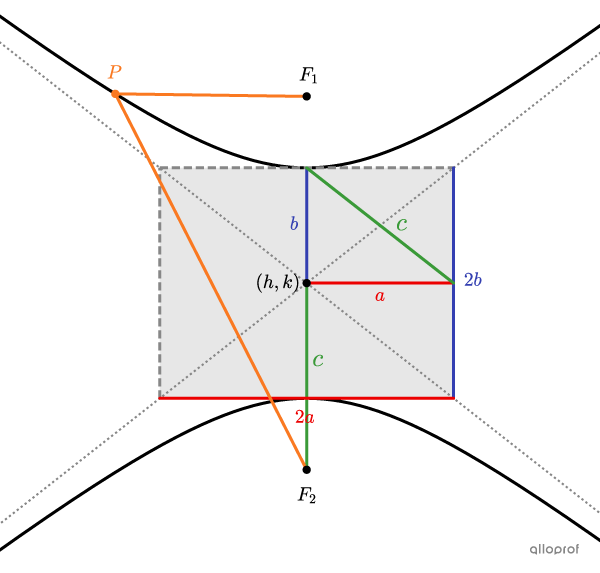
||\left \vert \text{m} \overline{F_1\color{orange}{P}} - \text{m} \overline{F_2\color{orange}{P}}\right \vert = \color{blue}{2b}\\ \color{red}{a^2}+\color{blue}{b^2}= \color{green}{c^2}||
|\dfrac{(x-h)^2}{a^2} - \dfrac{(y-k)^2}{b^2}= 1|
où
|\begin{align} a &:\text{la mesure entre le sommet et le centre}\\ b &: \text{la moitié de la hauteur du rectangle} \\ (h,k)&:\text{les coordonnées du centre}\\&\phantom {:}\ \ \text{(l'intersection des asymptotes)}\end{align}|
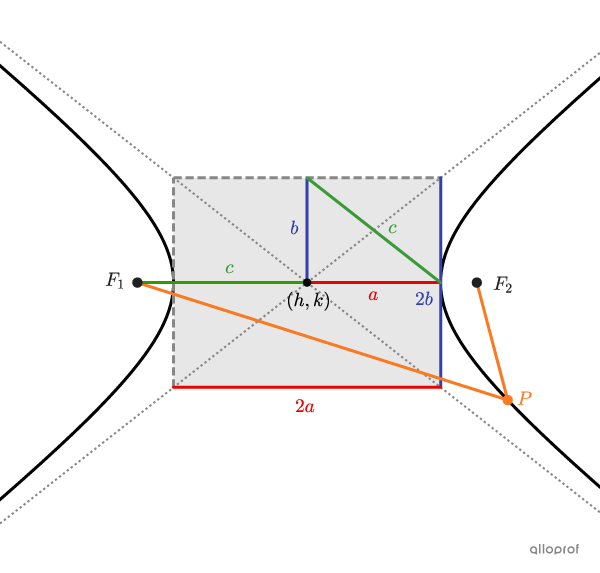
||\left \vert \text{m} \overline{F_1\color{orange}{P}} - \text{m} \overline{F_2\color{orange}{P}}\right \vert = \color{red}{2a}\\ \color{red}{a^2}+\color{blue}{b^2}= \color{green}{c^2}||
Le taux de variation des asymptotes équivaut à |\pm \dfrac{\color{blue}{b}}{\color{red}{a}}(x-h)+k.|
Finalement, Gitane décide de se rendre sur un cours d'eau un peu plus achalandé. À son grand malheur, elle constate qu'elle se fait dépasser par deux bateaux en même temps. Afin d'éviter de chavirer, elle doit déplacer son embarcation du point de rencontre des deux houles formées par les bateaux. On peut représenter le tout de la façon suivante.
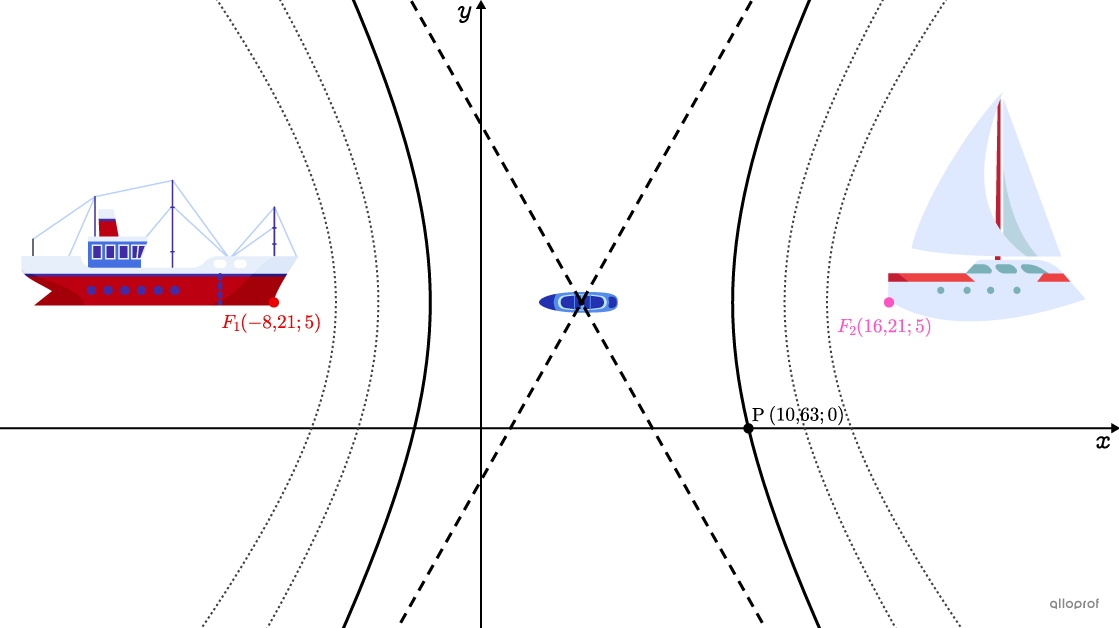
Avec ces données, détermine l'équation associée au modèle mathématique qui permettra à Gitane de mieux orienter sa navigation.
Il s'agit de résoudre un système d'équations en utilisant généralement la méthode de substitution.
Un peu tannée de la pêche, Gitane décide de se payer un voyage dans une région où il est possible d'aller faire du bateau avec des requins aux allures préhistoriques tels des dinosaures de mer. Avec l'eau qui est pratiquement transparente, elle peut les voir nager sans problème. Par contre, elle les perd de vue lorsqu'ils passent sous l'embarcation.
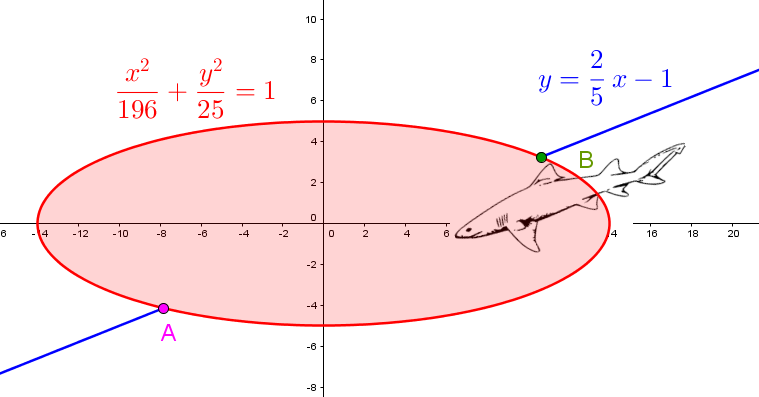
En tenant pour acquis qu'ils nagent en ligne droite à une vitesse de |5| m/s, détermine pendant combien de temps les requins sont sous le navire.
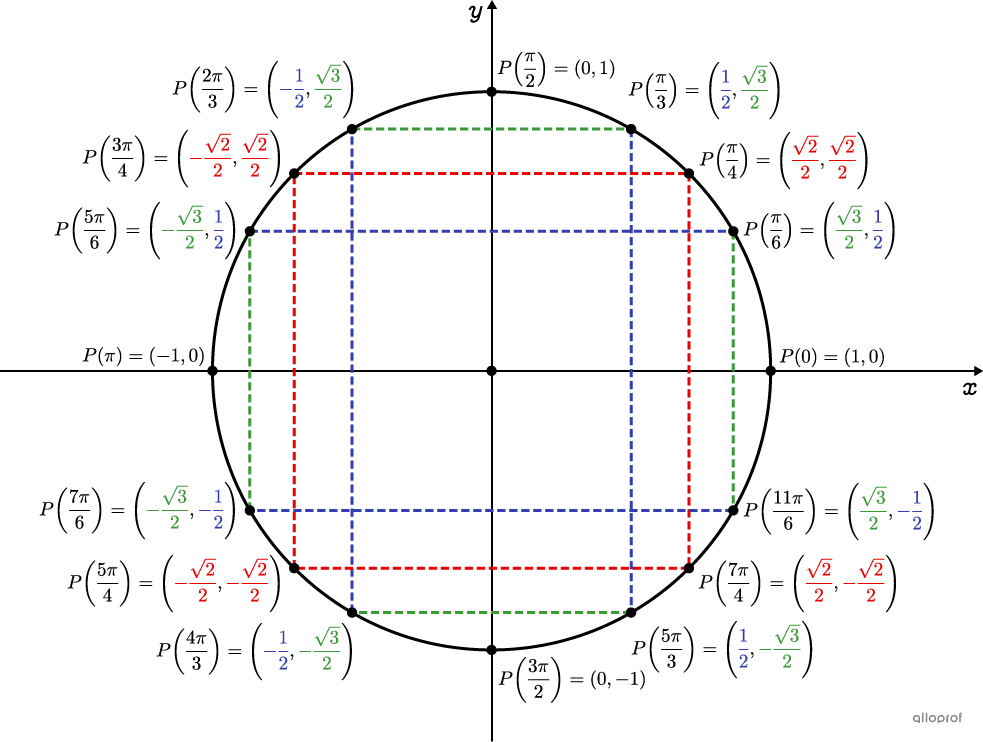
À partir de ce dessin, il est important de remarquer deux choses.
Les coordonnées des points de même couleur sont symétriquement liées.
Un tour complet du cercle |=2\pi\ \text{rad}.|
Quelle sont les coordonnées du point associé à un angle de |\dfrac{-17\pi}{4}?|